《给非数学专业人士 Lean 4 速成课》第一部分：出发！——“你好，证明”

第 1 章：为什么是 Lean？为什么是你？

1.1 一枚“非正式”的菲尔兹奖

2023年，数学界发生了一件“圈内地震”级的大事。

这件事不是某个古老的猜想又被证明了，而是数学界的“莫扎特”、菲尔兹奖（数学界的诺贝尔奖）得主陶哲轩，突然开始在他的个人博客上“直播”学习一个新工具¹。

这个工具不是 Matlab，不是 Python，也不是 R。它叫 Lean 4。

请注意，陶哲轩不是在“玩票”。他几乎是立刻就将这个新工具投入到了最前沿的战斗中：他与几位合作者一起，着手用 Lean 4 形式化一个他自己刚刚取得重大突破的“多项式弗赖曼-鲁萨猜想”（PFR 猜想）¹。

几个月后，事情变得更加有趣了。

陶哲轩在社交媒体上发帖，内容大致是：

“我用 Lean 4 形式化我最近的另一篇论文时，Lean 4 这家伙，指出了我的一个引理中……缺少了一个假设条件。”²

在另一篇关于 PFR 猜想形式化的博客中，他和合作者又发现了一个“一个小的但并非微不足道的错误”³。

请在这里暂停一秒钟，体会这句话的重量。

连陶哲轩——这个星球上最顶尖、最严谨的数学大脑之一——也会在自己的手稿中留下“小错误”。而 Lean 4，这个“程序”，扮演了他的“代码审查员”，并成功地抓到了这个 Bug。

这不只是一个“计算器”。这是一种全新的、能与顶尖人类智慧进行“对等协作”的工具。陶哲轩将它称为（未来）所有科学家的新计算器⁴。

那么，它和我们——“金色葡萄”们，这些程序员、工程师、生物信息学家、数据科学家——又有什么关系？

1.2 你最大的敌人是“认知失调”

好了，你被陶哲轩的故事“忽悠”了进来，兴冲冲地下载了 Lean 4。

然后，99% 的人会在 48 小时内愤怒地卸载它。

为什么？

因为你遇到了学习 Lean 4 最大的、也是最荒谬的障碍——“认知失调”。

心理学家利昂·费斯廷格在 1950 年代提出了这个理论。它指的是当你持有两个相互冲突的信念时，你感到的那种极度不适⁵。

对于你，一个“金色葡萄”（有经验的程序员或工程师）来说，这种冲突是灾难性的：

• 信念 A (自我认知): “我是一个聪明的、有能力的程序员。我能用 Python 搭建网站，能用 C++ 写出高效算法，我能理解复杂的技术文档。”
• 信念 B (残酷现实): “我打开这个叫 Lean 4 的鬼东西，对着屏幕奋战了三个小时，却无法向它证明 $1+1=2$。”⁶

这种挫败感是毁灭性的。你感觉自己受到了愚弄。

但这不是你的错！你只是掉进了一个持续了100年的“学术陷阱”。

1913年，两位顶尖的数学家与哲学家，罗素和怀特海，出版了鸿篇巨著《数学原理》。他们的伟大目标是：从最基础、最无可辩驳的公理出发，一步一步重建整个人类数学的大厦⁷。

你猜，他们花了多少篇幅才证明 $1+1=2$？

答案是：370多页⁷。

这就是问题所在！

传统的 Lean 4 教程，总是默认你也想成为一名“逻辑学家”，强迫你重走一遍罗素的苦旅。它们让你“用研究生级别的工具去证明 $1+1=2$”⁴。

这是一种智力上的霸凌。

你是一个“务实”的建造者⁴。你学习工具是为了“构建”应用，而不是为了“受虐”。当你被强迫去证明 $1+1=2$ 时，你感到的“认知失调”是完全合理、完全正当的⁸。你不是在“学习”，你是在“忍受”。

1.3 本书的“革命性”前提

本书将彻底规避这个陷阱。

我们的“革命性”前提是：我们将彻底分离“工具”与“数学”⁴。

你不需要知道 Lean 4 的“内核”⁹是如何用“依赖类型论”¹⁰定义“1”和“+”的。那就像你不需要知道 C++ 编译器是如何将你的代码转换成汇编语言一样。

你只需要知道如何使用它。

我们不废话，立刻来证明点“有用”的东西。

还记得你的中学代数“噩梦”（或者“乐趣”）吗？展开 $(a+b)^2$。

• 传统数学： 你需要在草稿纸上用“分配律”¹¹，一步步推导 $(a+b)(a+b) = a \cdot a + a \cdot b + b \cdot a + b \cdot b = a^2 + 2ab + b^2$¹²。
• Lean 4： 在我们的“证明实验室”里，你只需要输入：¹³

-- 导入“数学库” (就像 Python 里的 import numpy)
import Mathlib.Data.Real.Basic
-- 导入“代数专家” (一个自动化工具)
import Mathlib.Tactic.Ring

-- 陈述你的“目标”
example (a b : Real) : (a + b)^2 = a^2 + 2 * a * b + b^2 := by
  -- 使用“策略”
  ring -- 搞定！

看到了吗？ring 是一个“策略”。它是 Lean 4 庞大的数学库¹⁴中的一个“代数专家”¹⁵。你不需要知道它是怎么实现的，你只需要知道在中学代数中，何时使用它。

这才是 Lean 4 的“真面目”。

它不（仅仅）是“数学家的玩具”，它首先是一个强大的、可被验证的通用编程语言⁹。

你知道谁也在用 Lean 4 吗？不是只有陶哲轩。

亚马逊 AWS¹⁶。

亚马逊的工程师需要确保他们的云服务（比如 Amazon S3）的访问策略绝对安全、没有漏洞。他们用什么来保证？他们开发了一种叫 Cedar 的安全策略语言¹⁷。

而他们如何“证明” Cedar 语言本身是“绝对正确”的？

他们用 Lean 4 为 Cedar 建立了一个“可执行的形式化模型”，并用 Lean 4 证明了 Cedar 的核心安全属性¹⁶。

这才是 Lean 4 对你（程序员、工程师）的真正意义！它是一个工业级的“正确性引擎”¹⁸。它被用来验证那些“绝对不容许出错”的系统¹⁹。

1.4 “指挥家”的思维模式

让我们回到开头的“挂钩”。

证明 $(a+b)^2 = a^2 + 2ab + b^2$⁴。

和

证明“PFR 猜想”的某一步¹（甚至“黎曼猜想”的某一步²⁰）。

……在 Lean 4 中，到底有什么共同点？

答案是：它们使用的是完全相同的思维模式。

当你的“目标”是证明 $(a+b)^2 =...$ 时，你没有去（像中学生一样）“计算”，你（像一个指挥家一样）“调用”了 ring 策略。

当陶哲轩面对 PFR 猜想的某个复杂“目标”时，他也没有“从零计算”，他（像一个指挥家一样）“调用”了他需要的、可能比 ring 复杂一万倍的策略（比如 field_simp²¹ 或者他博客里提到的各种自定义战术²¹）。

你看，你们都在“指挥”。

Lean 4 的精髓，不在于成为一个“逻辑的苦力”，从 $1+1=2$ 开始一砖一瓦地盖房子。

Lean 4 的精髓，在于成为一个“证明的指挥家”。你要学会的，是如何“阅读乐谱”（看懂 Lean 4 的“目标”），以及何时“挥动指挥棒”（调用正确的“策略”）。

这，就是本书要教给你的。我们不学“数学悬崖”，我们只学“工具箱”。

学完本书，你将抵达你的“B点”：你将能熟练使用 Lean 4 工具本身，并有绝对的信心，借助 AI + Lean 4，去攻克你自己专业领域（无论是生物统计、金融模型还是 AI 安全²²）的高等数学问题⁴。

准备好了吗？

让我们出发，搭建你的“证明实验室”。

第 2 章：搭建你的“证明实验室”

2.1 你的“实时编译器”

好了，欢迎来到“车间”。在上一章，我们见识了 Lean 4 的“威力”——它既是陶哲轩的“代码审查员”，也是亚马逊 AWS 的“正确性引擎”。现在，我们要把它变成你的工具。

对于你，一个经验丰富的程序员（“金色葡萄”），最好的类比已经摆在你面前了²³：

Visual Studio Code (VS Code) 是你的 IDE，而 Lean 4 是你的“实时编译器”。

但请等一下，这个“编译器”和你以前用过的任何东西都完全不同。

它不是像 gcc 或 javac 那样，在你洋洋洒洒写下 500 行代码，点击“构建”后，才姗姗来迟地甩给你一堆“编译失败”错误的“事后诸葛亮”。

不，Lean 4 更像是一个时刻坐在你旁边的、既懂编程又懂数学的“高级结对程序员”。它是一个“实时”的、“对话式”的伙伴²⁴。

你每敲一个字，这个“伙伴”都会通过一个神奇的窗口（我们稍后会认识它）实时地告诉你：

• “嗯，你这步逻辑走得通。”
• “很好，现在你的下一个目标是证明这个。”
• “等等……你这里有个漏洞。你声称 x > 0，但你忘了考虑 x=0 的情况！”
  本章的目标，就是把你平平无奇的电脑，组装成一个功能齐全、响应实时的“证明实验室”。我们将安装它的“工作台”，激活它的“魔法核心”，并启动你的这位新“副驾驶”。

2.2 快乐学习的“零摩擦”环境

一个顺滑的环境是快乐学习的开始²⁵。

让我们面对一个残酷的现实：这个世界上 90%“最好的工具”之所以被你（一个“金色葡萄”）放弃，根本不是因为它“不够强大”，而是因为它死在了“安装地狱”之中。

这，就是“认知失调”的第一个、也是最致命的陷阱。

当你，一个能用 Ansible 配置复杂 Docker 集群、能调试 C++ 内存泄漏的资深工程师，却被一堆“路径错误”、“依赖冲突”或“版本不兼容”搞得焦头烂额时……你感受到的那种挫败感是真实且毁灭性的。

你的“信念 A”（“我是个有能力的工程师”）和“信念 B”（“我连这个工具的‘Hello World’都跑不起来”）发生了剧烈冲突²⁶。

本书承诺：我们将彻底规避这个陷阱。

正如我们在第一章绕过了 1+1=2 的“学术苦旅”，我们这一章也将绕过所有“手动编译”、“配置环境变量”的“安装苦旅”。

我们的目标是“零摩擦”。因为你是“证明的指挥家”，你的 100% 的宝贵精力，都应该花在“指挥”乐团上，而不是在后台“修理漏水的管道”。

2.3 “实验室”组件安装指南

别担心，我们的“实验室”组件清单非常简洁。它由四个核心组件构成：

1. 工作台: VS Code (你的 IDE)²⁷。
2. 魔法核心: Lean 4 插件 (它会自动搞定一切)²⁴。
3. 工具链管理员: elan (它管理 Lean 的版本)²⁶。
4. 项目管家: lake (它构建你的项目)²⁸。
   这个组合听起来是不是很熟？没错。如果你用过 nvm / pyenv / rustup ，并且用过 npm / cargo / pip ，你已经 100% 知道接下来要发生什么了。

第一步：安装“工作台” (Visual Studio Code)

这是我们最简单的一步。Lean 社区和核心开发团队，已经把宝全押在了 VS Code 上。Lean 4 和 VS Code 的集成是目前体验最好的²⁷。

1. 前往 VS Code 官网 (https://code.visualstudio.com/) 。
2. 下载并安装适用于你操作系统的版本（Windows, macOS, Linux 均可）。
   我们选择 VS Code，不仅仅因为它是一个“文本编辑器”。它的插件系统是 Lean 4 “实时”体验的核心。我们稍后要激活的那个“副驾驶”窗口，并不是一个独立的程序，而是深度集成在 VS Code 界面内的²⁹。

第二步：安装“魔法核心” (Lean 4 插件)

现在，启动你刚刚安装的 VS Code。我们要来安装那个“会施法”的插件。

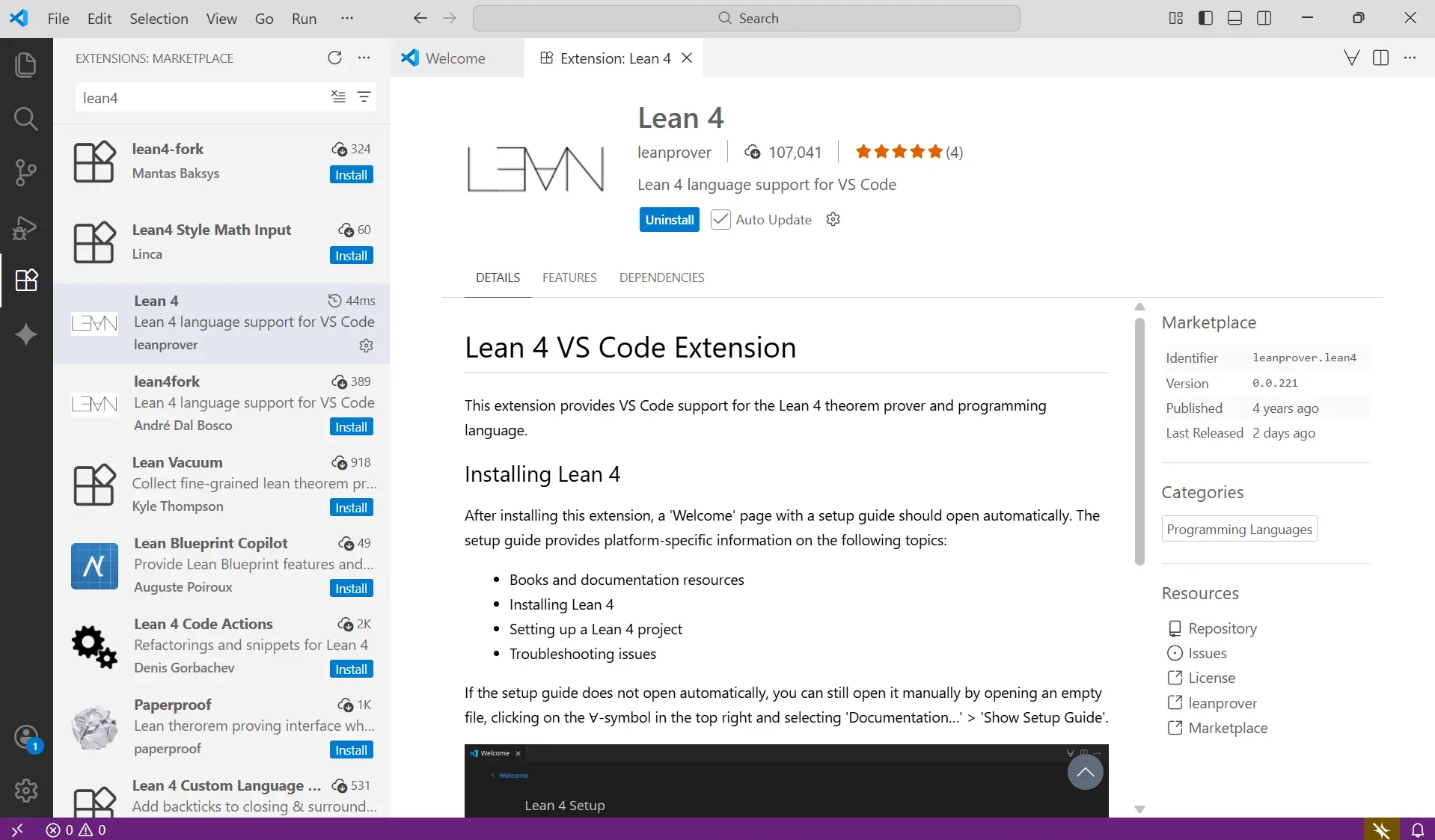
1. 在 VS Code 的左侧边栏，点击那个“扩展”图标（四个方块，其中一个分离了）。
2. 在顶部的搜索框中，输入 lean4。
3. 请仔细看！ 你会看到几个搜索结果。请选择那个发布者是 leanprover、名字是 lean4 的官方插件²⁴。它的全名是 leanprover.lean4。
4. 就是它。点击蓝色的“Install”按钮。

第三步：激活“工具链管理员” (elan)

魔法时刻来了。

你以为你现在需要打开浏览器，去搜索“如何下载 Lean 4”，然后手动下载一个 .zip 或 .exe 文件？

不。我们是“指挥家”，我们不干这种体力活。

安装完插件后，VS Code 可能会自动弹出一个“欢迎”页面或一个小的提示框²⁹。如果你没看到，也别担心。

核心步骤： 当你（在第四步）第一次创建或打开一个 Lean 项目文件（后缀为 .lean）时，lean4 插件会自动检测到你的电脑上“没有安装 Lean 4 工具链”²⁵。

然后，它会主动弹出一个提示框，大意是：“我没找到 Lean。你要我帮你安装吗？”

你只需要，带着“指挥家”的从容，点击那个“是” (Yes) 或“安装” (Install) 按钮。

【“金色葡萄”的专属幕后揭秘】
当你点击“是”时，插件到底在干什么？它在为你自动下载和安装一个叫 elan 的小工具³⁰。

• elan 是什么？ 它是 Lean 的官方“工具链管理器”³¹。
• 最好的类比： elan 之于 lean，就如同 nvm 之于 Node.js，pyenv 之于 Python ，或者 rustup 之于 Rust 。
• 这为什么重要？ 这意味着你永远不需要“手动”安装 Lean 4。elan 会为你处理一切，包括未来在不同项目间自动切换不同版本的 Lean²⁶。
• 我们避开的“陷阱”： 那些“传统”教程³²此时会让你打开终端，去运行一行天书般的 curl 或 powershell 脚本来手动安装 elan。我们为什么要这么做？让插件服务我们！这才是“零摩擦”。

第四步：创建你的“项目管家” (lake)

好了，我们的“工作台” (VS Code) 和“魔法核心” (Lean 4 插件 + elan) 都有了。现在，我们需要一个“项目”来存放我们的“乐谱”³³。

在 Lean 4 的世界里，我们使用一个叫 lake 的工具来管理项目²⁸。

• 最好的类比： lake 之于 lean，就如同 npm 之于 Node.js，cargo 之于 Rust，或者 pip/poetry 之于 Python。它负责处理依赖、构建和运行。

让我们在 VS Code 内部完成这一切：

1. 打开 VS Code 的集成终端。

   • 如何操作： 点击 VS Code 顶部菜单栏的 Terminal -> New Terminal。
   • 注意如果你刚刚安装Lean 4 插件 + elan，应当重启vscode，否则可能后续lake命令无法识别。

2. 一个终端窗口会出现在 VS Code 底部。cd 到一个你喜欢放代码的地方 (比如 Documents 或 Projects)。

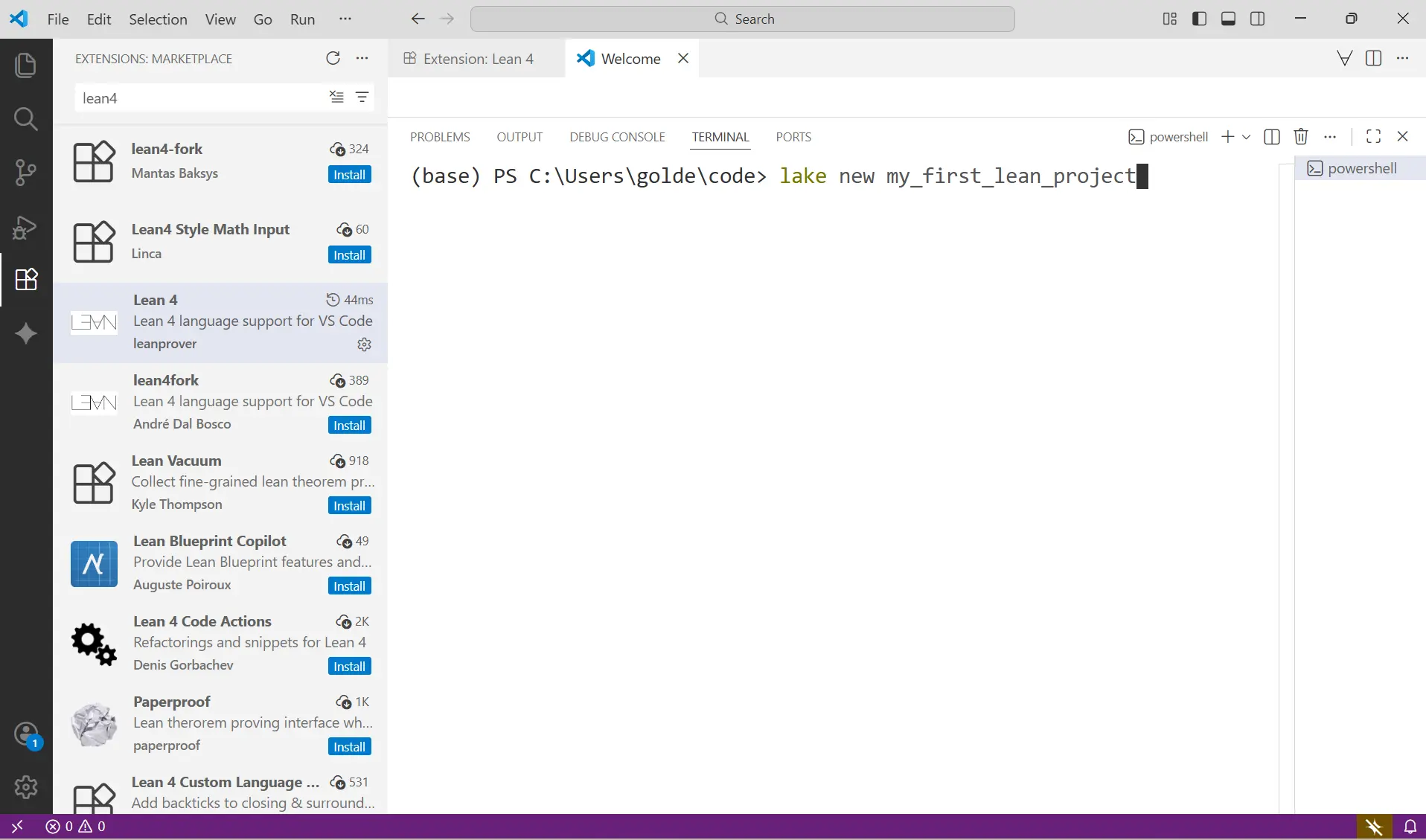
3. 运行以下命令，来创建你的第一个 Lean 4 项目：³³

   lake new my_first_lean_project
   

   (这个命令会创建一个名为 my_first_lean_project 的新文件夹，并在里面设置好一切)

【“金色葡萄”的专属陷阱回避】

• lake 其实有两个很像的命令：lake new 和 lake init。
• lake init 会在当前文件夹初始化项目，这非常容易把你的文件结构搞得一团糟³⁴。
• lake new <name> 会为你创建一个全新的、干净的文件夹 <name>，然后把项目文件放进去³⁴。
• 结论： 永远使用 lake new。我们又一次在不经意间，避开了一个足以引发“认知失调”的小陷阱。

继续我们的行动：

1. 现在，我们需要“打开”这个新创建的项目。在终端里运行：

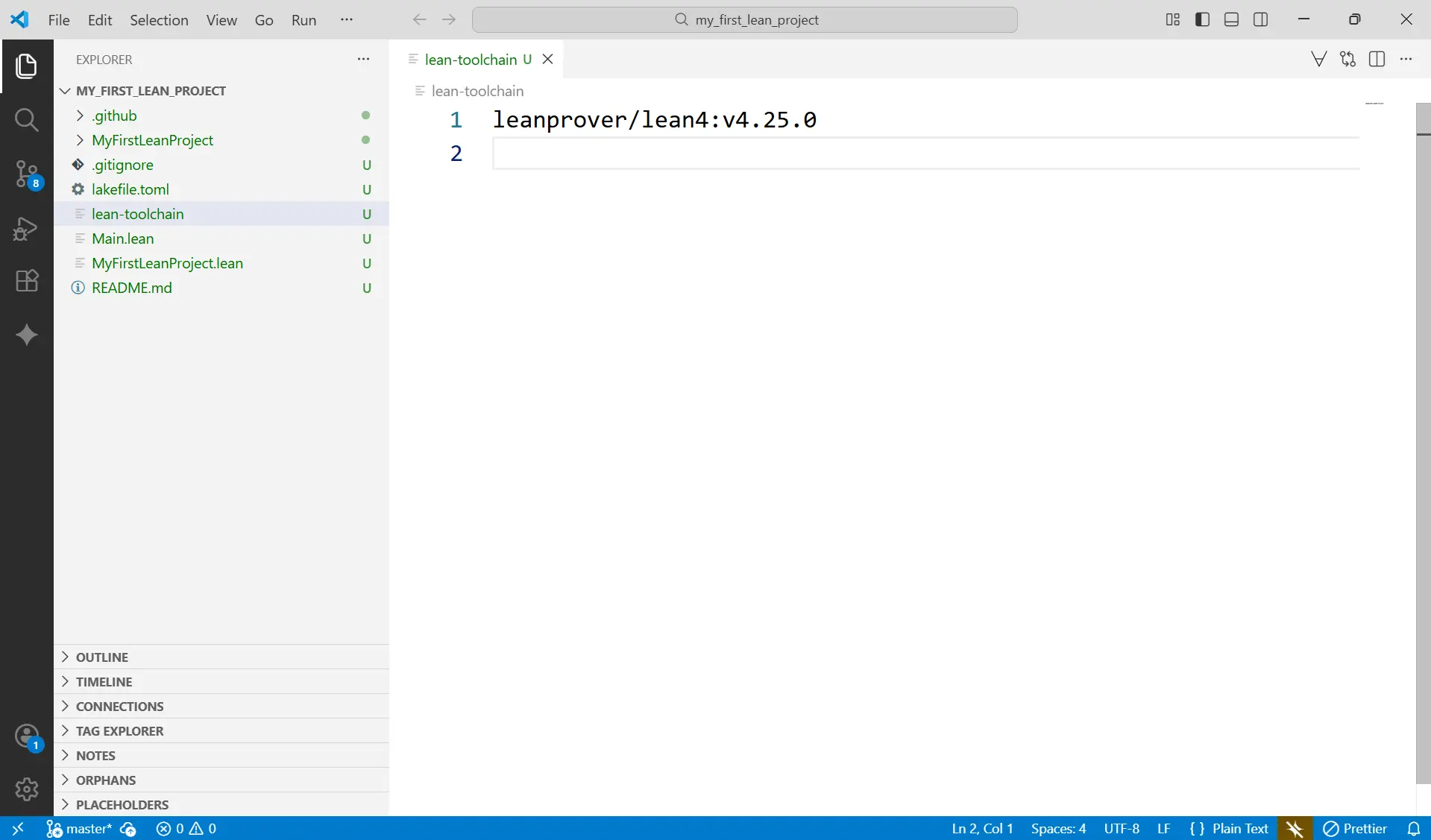
   cd my_first_lean_project
   code .
   ```    (这个 `code .` 命令会告诉 VS Code 在当前文件夹（即你的新项目）中打开一个新窗口。你也可以用顶部菜单的 File -> Open Folder... 来手动打开那个文件夹。)
   

2. 认识你的项目： 在 VS Code 左侧的文件浏览器中，你会看到 lake 已经为你创建的标准结构³⁵：
   • my_first_lean_project/
   • Main.lean: 你的“主”文件。我们马上就会用到它。
   • lakefile.lean: 你的“项目配置文件”(类似 package.json 或 Cargo.toml)。
   • lean-toolchain: 关键！ 这是一个纯文本文件，它告诉 elan 这个项目需要哪个版本的 Lean。这就是 elan 实现“项目隔离”的“魔法”²⁶。

第五步：认识你的新“副驾驶” (Infoview)

这是本章最重要的时刻。欢迎认识你的“副驾驶”——Infoview (信息视图)³⁶。

行动：

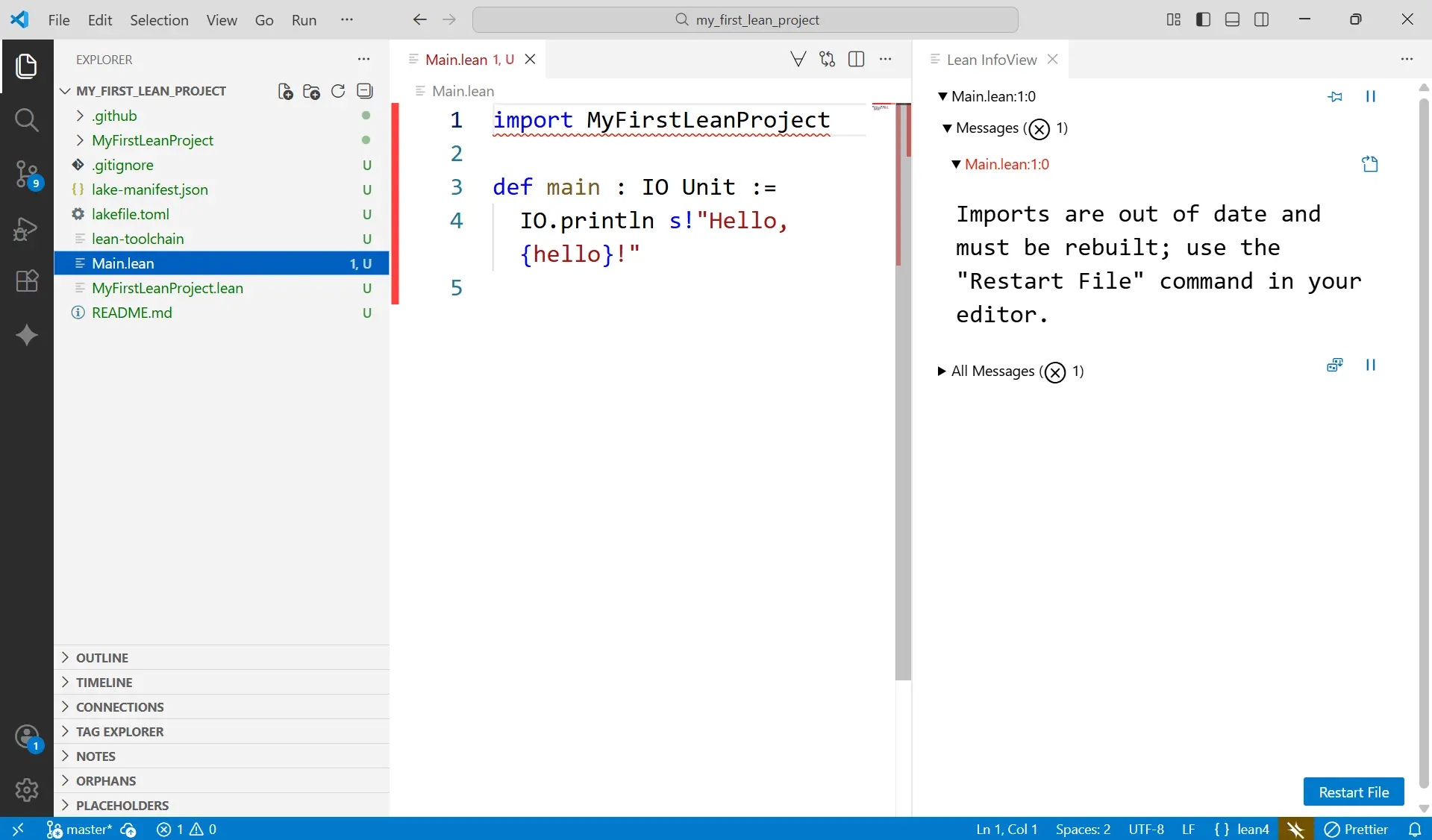
1. 在 VS Code 的文件浏览器中，点击打开你刚刚创建的 Main.lean 文件。
2. （如果你在第三步还没有安装 Lean，这时 lean4 插件会检测到 lean-toolchain 文件，并自动开始下载和安装正确的 Lean 版本³⁰。耐心等待它几分钟，VS Code 底部状态栏会显示进度。）

我们的第一次“对话”：

Main.lean 文件里可能有一些默认的 "Hello, world!" 代码³⁷。它们是给“程序员”准备的，我们暂时先无视它。

让我们来一次“计算器”检查。把你的光标移动到文件的最底部，另起一行，输入这行“魔法指令”：

#eval 18 + 19

见证奇迹：

当你的光标停留在这行时，立刻去看你的“副驾驶”窗口 (Infoview)！

它应该会立刻显示出 37³⁶。

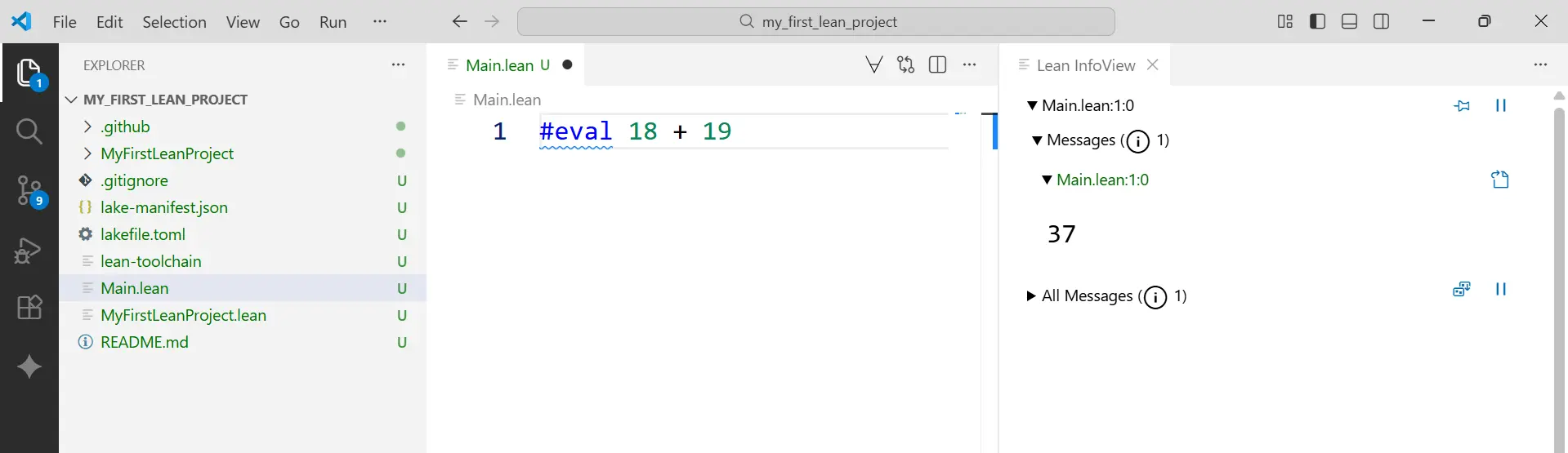
这，就是“热启动”。你的 IDE 正在和 Lean 4 进行“实时对话”。#eval 是你对 Lean 说的：“嘿，帮我算个数。” Infoview 就是 Lean 的回答。

2.4 着陆：“目标达成! 🎉”

#eval 只是一个“计算器”检查。我们的目标是“证明”。

是时候对我们的“实验室”进行最后的“校准”了。我们要让 Lean 4 亲口说出那句我们在大纲里承诺过的话³⁷。

行动：

1. 清空画板： 删掉 Main.lean 文件里的所有内容。是的，全部删掉。我们要一个干净的“乐谱”。

2. 输入你的第一个“目标”： 粘贴或输入以下这行代码。这是我们的“你好，证明！”。

   example : 2 + 2 = 4 := by rfl
   

最终的“Wow!”时刻：

行动：

1. 不要做任何事。
2. 把你的鼠标光标，移动到 rfl 这三个字母上，或者移动到这一行的末尾。
3. 现在，请屏住呼吸，盯着你的 Infoview 窗口。

你看到了什么？

你不会看到 37。你很可能会看到一行朴实无华的字：

No goals

（在某些老版本或者配置下，它可能显示 goals accomplished）³⁸。

但是，这还不是全部！请把你的视线移回代码编辑器。在 example 这一行的行首（或者根据你的 VS Code 插件配置²⁴），你应该会看到一个小的、令人愉悦的图标：

🎉 (或者一个 ✔️✔️ 双勾)

在 Infoview 窗口的某个地方，你也会看到那句我们梦寐以求的祝贺：

"Goals accomplished! 🎉"²⁹

恭喜！你的“证明实验室”已正式投入运营。

我们来回顾一下这个“奇迹”：

• 你没有去证明 1+1=2。
• 但你确实用你的“实验室”，让 Lean 4 验证了 2+2=4。
• 你没有花 370 页。
• 你只用了三个字母：rfl。
  这感觉如何？
  这不是“认知失调”。这是“掌控感”。
  你的实验室已经搭建完毕，你的“副驾驶”已经就位。在下一章，我们将正式开始我们的“对话”——我们将解密，你刚刚挥舞的这根“魔法棒” rfl，到底是什么。

第 3 章：你的第一个证明： 2+2=4

3.1 挂钩：一次“失败”的价值

在上一章的结尾，你成功组装了“证明实验室”，并见证了你的第一个“Wow!”时刻³⁹。你输入了 example : 2 + 2 = 4 := by rfl，你的新“副驾驶”（Infoview）立刻欢呼：“Goals accomplished! 🎉”⁴⁰。

这感觉很棒。但这只是硬币的一面。

这立刻引出了一个更深刻、也更重要的问题：在 Lean 4 中，证明 2 + 2 = 4 和证明 2 + 2 = 5 到底有什么区别？

对于你，一个“金色葡萄”（经验丰富的程序员），你内心深知一个残酷的真相：一个只会说“是”的编译器或“结对程序员”是毫无价值的⁴¹。一个单元测试如果永远通过，那它什么也没测试。你系统的价值，恰恰在于它能拒绝无效的输入。

本章，我们将故意“犯错”。我们将看到 Lean 4 如何“拒绝”我们的错误断言。而它的“拒绝”方式，远比它“同意”的方式，更能体现它的真正力量。

3.2 论点：欢迎来到“对话框”

是时候升级我们的核心隐喻了。Lean 4 是一个“对话式”证明器⁴²。

你的工作不是像写 Java 或 Python 那样，单向地“写代码”然后“运行”。你的工作是和 Lean 4 “聊天”，直到你（和它）都对结果满意，直到你的“目标”消失⁴³。

在第 1 章，我们说你是“证明的指挥家”。在第 2 章，我们说 Lean 4 是你的“副驾驶”。现在，我们把它们合而为一：

1. 你的“议题”：example : 2 + 2 = 4 :=... 这行代码，是你（指挥家）对乐团（Lean 4）提出的“演奏议程”。
2. by 关键字：这就是你按下“对讲机”按钮的动作。从这一刻起，你进入了“策略模式”⁴⁴。你不再是“独白”，你开始了“对话”。
3. Lean 的“倾听”：一旦你按下 by，你的“副驾驶”—— Infoview 窗口——会立刻显示 1 goal...。这是 Lean 在回应：“收到。这是我们当前的目标。我该怎么做？”
4. 你的“发言”：你在 by 后面输入的任何东西（比如 rfl），都是一个“策略”。这是你对 Lean 的指令⁴⁵。
5. Lean 的“回应”：Lean 会立刻执行你的指令，并更新 Infoview。它要么显示一个新的目标（如果证明没完成），要么显示“Goals accomplished! 🎉”（如果完成了），要么……显示一个错误。
   现在，让我们开始这场对话。

3.3 支持：refl 的“显而易见”

我们将逐帧慢放你在第 2 章结尾处的操作，来体验这场“对话”的每一个细节⁴⁶。

步骤一：提出议程（看见目标）

请在你的 Main.lean 文件中，清空所有内容，然后只输入这一行（暂时不要加 rfl）：

example : 2 + 2 = 4 := by

现在，把你的鼠标光标，移动到 by 关键字的后面。

请立刻盯住你的“副驾驶”—— Infoview 窗口。它不再是空的。它现在显示着你的第一个“证明状态”⁴⁴。

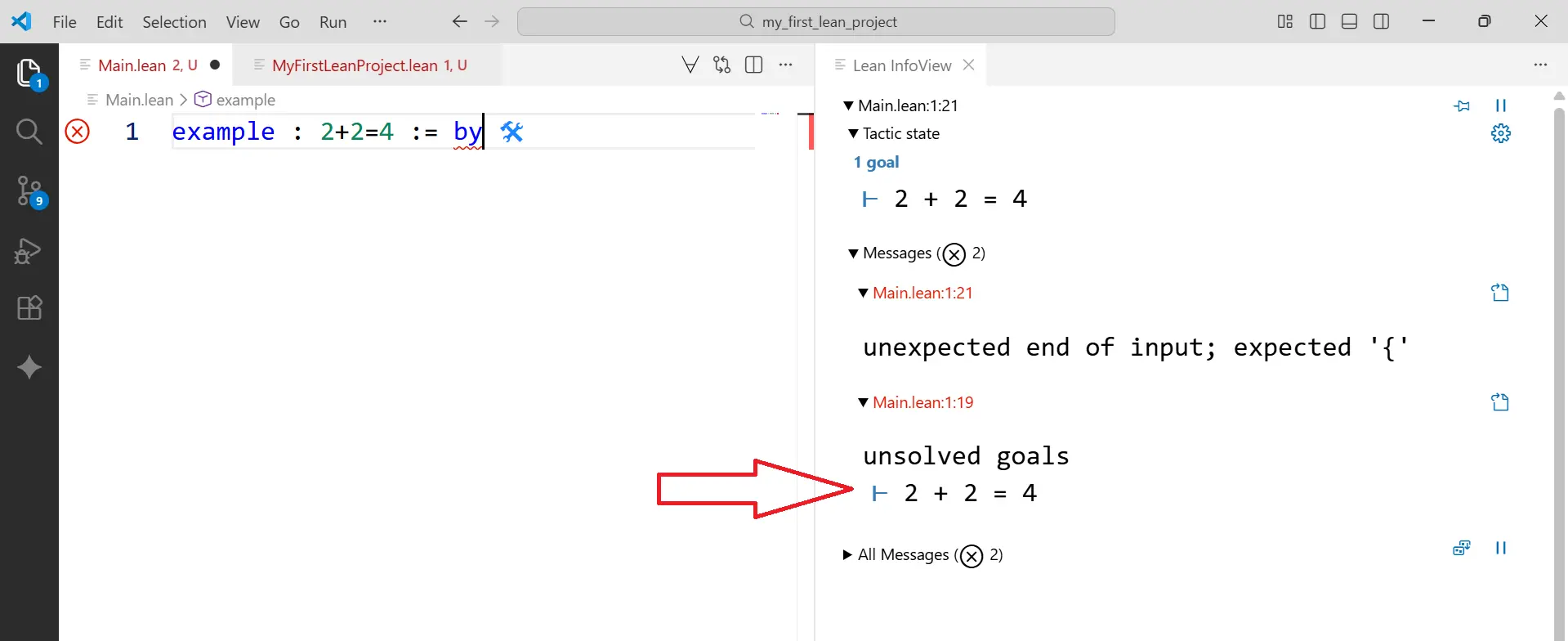
那个 ⊢ 符号（你可以就叫它“目标符号”）是 Lean 在对你说：“收到。我确认，我们当前的目标是证明 2 + 2 = 4。请指示。”

步骤二：你的第一个“魔法词” (The Tactic, refl)

现在，在 by 后面，输入这三个字母：rfl。

rfl 是什么？它不是一个随机的缩写。它代表 Reflexivity，即“自反性”⁴⁷。

在数学中，“自反性”是说“任何东西都等于它自己”（比如 a = a）。这听起来像一句平平无奇的废话，但在 Lean 4 里，这是最有用的“废话”之一。

隐喻： rfl 策略，就是你对 Lean 说的“这还用问吗？”或“这显而易见！”。你是在授权 Lean 4 自己去检查一下。

【“金色葡萄”的专属幕后揭秘：rfl 到底在干什么？】
当你（程序员）使用 rfl 时，你并不是在“教”Lean 4 如何做加法。你是在命令它执行一个你非常熟悉的算法：

1. 拿到目标： Lean 看到目标是 LHS = RHS（即 2 + 2 = 4）。
2. 求值 LHS： Lean 像一个计算器一样，把 2 + 2 计算到底，得到结果 4。
3. 求值 RHS： Lean 把 4 计算到底，结果还是 4。
4. 比较： Lean 现在比较这两个计算结果。它看到的不再是 2 + 2 = 4，而是 4 = 4 。
5. 确认： 4 = 4 吗？是的，这符合“自反性”(a = a)。rfl 策略成功！
   这就是大纲里说的“亲眼看着‘目标’从 2 + 2 = 4 变成 4 = 4”。这个过程快到你肉眼看不见，但 rfl 确实是这样做的。它检查的是“定义相等性”⁴⁴。

步骤三：Lean 的“回应” (成功)

当你输入 rfl 后，甚至不需要按回车。奇迹发生了。

Infoview 里的 1 goal ⊢ 2 + 2 = 4... 消失了⁴⁸。

取而代之的，是那句甜美的祝贺：“Goals accomplished! 🎉” （或者在某些配置下是 "No goals"，意思是“你没别的活儿要干了！”）。

同时，在你的代码编辑器里，example 这一行前面的“小灯泡”或“图标”变成了 ✔️✔️ 或 🎉，确认了这一行代码的逻辑是完整的⁴⁹。

这场“对话”结束了。你提出了议题 (2+2=4)，Lean 4 确认了目标 (⊢ 2+2=4)，你给出了策略 (rfl)，Lean 4 执行并确认 (🎉)。

步骤四：高能时刻——“对话”的真正意义 (失败)

好了，“你好，世界”结束了。让我们来做点真正有意义的事。

让我们对 Lean 4 撒个谎。

删掉刚才那行，或者在它下面另起一行，输入这个“明显错误”的命题：

example : 2 + 2 = 5 := by

和刚才一样，把光标放在 by 后面。Infoview 同样会显示一个目标：1 goal ⊢ 2 + 2 = 5。

到目前为止，Lean 4 只是在“倾听”，它不会评判你的议题是真是假。它只是在说：“收到。我的目标是证明 2 + 2 = 5。请指示。”

现在，让我们用同样的“魔法词”。在 by 后面输入 rfl。

example : 2 + 2 = 5 := by rfl

这一次，“Goals accomplished”没有出现。rfl 这三个字母下面出现了一条愤怒的红色波浪线。你的“副驾驶”（Infoview）亮起了红灯。它在拒绝你。

但请仔细看它的回应。它没有“崩溃”，没有“空指针异常”。它给出了一个极有价值的、有逻辑的回应⁵⁰：

Tactic `rfl` failed: The left-hand-side
  2 + 2
is not definitionally equal to the right-hand-side
  5

它甚至会（在某些版本的提示中）直接告诉你它看到了什么：它把 2 + 2 计算成了 4，然后去比较 4 = 5，最后失败了⁴⁴。

【 插图要求 2 标题： Lean 4 的“否决” 左侧 (代码编辑器)： example : 2 + 2 = 5 := by rfl。rfl 三个字母被红色波浪线高亮。 右侧 (Infoview)： 清晰地显示错误信息。高亮 The rfl tactic failed 和 The arguments... are not equal。 标注： “这不是一个 Bug，这是特性！Lean 4 在告诉你：‘我无法证明这一点。’” 】

3.4 着陆：你的第一次“否决”

恭喜！你刚刚完成了你的第一个数学证明 (2+2=4)。

但更重要的是，你刚刚收到了你的第一个“否决”。

这个“否决”（2+2=5 失败）远比 2+2=4 的“成功”更有价值。

为什么？

因为它证明了你的“副驾驶”没有打瞌睡⁴¹。它在实时地、严格地审查你的逻辑。它就是陶哲轩所依赖的那个“代码审查员”，它就是亚马逊 AWS 用来确保系统万无一失的那个“正确性引擎”。

你刚刚亲手验证了：这个工具值得信赖。

这，就是“对话”的意义。你证明了“正确”是容易的，而“错误”是不可能的（至少用 rfl 是这样）。你的实验室不仅能运行，而且很安全。

现在，rfl（“这显而易见！”）是你的第一个“词汇”。在下一章，我们将学习如何在这场对话中，说出更复杂的句子。

引用的文献