昨天发布了近视度数与眼轴长之间的关系(数值模拟版)
后,有专家留言说这是有公式的。于是我打算今天推导一下。
我们将使用的是光线传输矩阵,或者叫ABCD矩阵的方法。这个方法非常简单直观,四则运算里只用乘法。虽然是一大堆连乘,但具体计算过程当然是交给初中二年级就会用的wolframcloud。
ABCD矩阵
这是用在近轴近似的条件下,所有的角度都很小,所以不仅sin(α)近似等于α, tan(α)也近似等于α
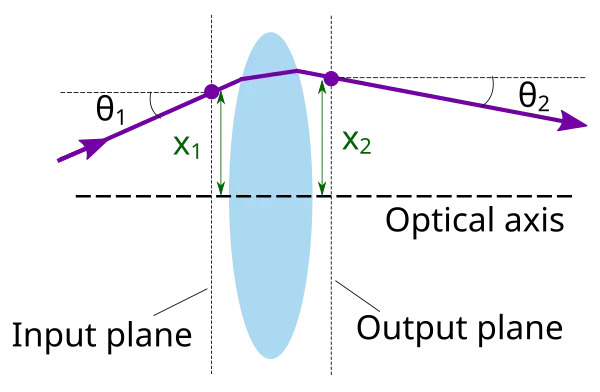
光线穿过一个光学系统的过程可以用一个2x2的矩阵来表示, 如果:
- 入射光线距离光轴是x1, 角度是 θ1,
- 出射光线距离光轴是x2, 角度是 θ2,
那么:
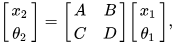
对于不同的光学元件, ABCD的取值不同:
- 在均匀介质的自由空间中传播,矩阵是:
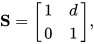
- 薄透镜:
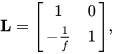
- 球面界面:
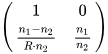
我们就用这仨就足以描述Gullstrand模型眼了。
(*常用ABCD矩阵*)
FreeSpace[d_] := {{1,d},{0,1}};
ThinLens[p]:={{1,0},{-p/1000,1}};
CurvedInterface[R_,n1_,n2_]:={{1,0},{(n1-n2)/(R*n2), n1/n2}};
建立模型眼
除了描述近视度数的综合验光仪用薄透镜,其他各个面就都是简单的球面界面。直接代入参数就行了。
(*折射率*)
nCornea = 1.376;
nHumor = 1.336;
nVitreous = 1.336;
nLens = 1.386;
nLensCore = 1.406;
nAir=1;
(*各表面*)
phoropter[p_] =ThinLens[p];
corneaFront = CurvedInterface[7.70, nAir, nCornea];
corneaBack = CurvedInterface[6.8, nCornea, nHumor];
lensFront = CurvedInterface[10, nHumor, nLens];
lensCoreFront = CurvedInterface[7.91, nLens, nLensCore];
lensCoreBack = CurvedInterface[-5.76,nLensCore, nLens];
lensBack = CurvedInterface[-6, nLens, nVitreous];
光线追迹
ABCD矩阵的用法就是连乘,但要注意方向,每一次光线传播都是放在 左乘
我们先整理一下光线传输的过程:
- 平行入射光,我们设定入射光线距离光轴是h, 平行光所以角度是0:
{h,0} - 通过phoropter:设定其屈光度为p:
phoropter[p] - 自由行进镜片到角膜顶点距离12mm:
FreeSpace[12] - 穿过角膜前表面:
corneaFront - 自由行进角膜厚度0.55mm:
FreeSpace[0.55] - 穿过角膜后表面:
corneaBack - 自由行进前房深度3.6mm:
FreeSpace[3.6] - 穿过晶体前表面:
lensFront - 自由行进晶体前皮质厚度0.546mm:
FreeSpace[0.546] - 穿过晶体核前表面:
lensCoreFront - 自由行进晶体核厚度2.419mm:
FreeSpace[2.419] - 穿过晶体核后表面:
lensCoreBack - 自由行进晶体后皮质厚度0.635mm:
FreeSpace[0.635] - 穿过晶体后表面:
lensBack - 自由行进玻璃体腔厚度d:FreeSpace[d]
最后光线到达视网膜的位置。上述过程用ABCD矩阵描述,就是乘起来
(*传输连乘*)
outputBeam=FreeSpace[d].lensBack.FreeSpace[0.635].lensCoreBack.FreeSpace[2.419].lensCoreFront.FreeSpace[0.546].lensFront.FreeSpace[3.6].corneaBack.FreeSpace[0.55].corneaFront.FreeSpace[12].phoropter[p].{h,0}
得到的结果,上面一项是光线与视网膜交点到光轴之间的距离,下面一项是夹角。

聚焦求解
所谓平行光聚焦到视网膜上的“聚焦”,就是说光线到达视网膜时,落在了光轴上,也就是上面这一项等于0
0.736669 +d (-0.0436408-0.000159918 p)-0.014452 p==0
你可以根据验光度数p求玻璃体厚度d,也可以反过来根据玻璃体厚度d求解近视度数p,因为我们更多需要知道的从眼轴长映射到屈光度,所以用d求解p:
Solve[outputBeam[[1]][[1]]==0,p]
得到
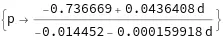
因为已知玻璃体厚度d与眼轴长AL的关系是:
AL=0.55+3.6+0.546+2.419+0.635+d= 7.75+d
所以只需要把上述结果中的d,用AL-7.75替换掉,就得到了屈光度与眼轴的计算公式:

你也许会说,这个结果不是线性的呀,跟昨天的数值分析好像差异很大,但其实如果我们画图,会发现其实还是挺直线的。
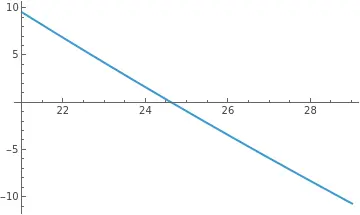
Solve[outputBeam[[1]][[1]]==0,p][[1]]
%/.d->AL-7.75//Simplify
AL2P[AL_]=p/.%
Plot[AL2P[AL],{AL,21,29}]
Series[AL2P[AL],{AL,24,1}]
如果把上述公式用一阶泰勒展开可以得到
P = 1.61322 - 2.57461*(AL-24)
也就是说,在24mm眼轴长附近,每1mm眼轴长变化,大约对应-2.57D近视度数变化。
