这一部分有Gemini动态视图演示： https://gemini.google.com/share/1ab841146427

序言：打破你办公室里的“黑箱”——致 Dr. X

让我们从一个你我都无比熟悉，却又常感无力的场景开始。

周二下午，一名 LASIK 术后三个月的患者坐在你的诊室里。他的视力表检查结果是完美的 1.0 (20/20)，但他看起来并不开心。

“医生，”他抱怨道，“白天还好，但一到了晚上，路灯周围全是那一圈圈奇怪的光晕，就像车灯炸开了一样。我根本没法开车。”

你点了点头，熟练地安排了一次波前像差检查。几分钟后，打印机吐出一张色彩斑斓的图表。你的手指划过上面密密麻麻的数据，最后停在一个红色的数字上：

你松了一口气，指着那个数字对病人解释说：“看，这就是问题所在。这叫做‘球差’（Spherical Aberration）。你的数值偏高，这就是导致眩光的原因。”

病人迷茫地看着你：“好的，医生。但‘球差’到底是个什么东西？为什么这个数字高了，我的车灯就会炸开？”

这一刻，诊室里的空气凝固了。

作为一名受过严格专业训练的眼科专家，你脑海中瞬间闪过教科书上的定义：“边缘光线与中心光线汇聚点不同……”或者更糟糕的数学定义：“它是 Zernike 多项式的第四阶径向项……”

但你发现，你无法让他看见你所知道的。

更诚实地说，有时候看着那些复杂的角膜地形图（Topography）、OCT 的断层扫描或是高端 IOL 的衍射环设计图，连我们自己也会在深夜怀疑：我真的懂它吗？还是我只是背下了“$Z_4^0$ = 眩光”这个公式？

房间里的大象：高科技的“黑箱”

欢迎来到现代眼科的悖论：我们被世界上最先进的光学设备包围——OCT、波前像差仪、飞秒激光、衍射型多焦 IOL——但它们对我们来说，往往只是昂贵的“黑箱”。

权威研究指出，这种“黑箱问题”正在成为医生信任和决策的最大障碍。我们把病人的角膜数据“喂”进机器，机器把手术方案“吐”出来。至于中间发生了什么？那是光学工程师的事。

为什么我们不敢打开这个黑箱？

因为守在黑箱门口的，是一条叫做“傅里叶光学” (Fourier Optics) 的恶龙。

对于绝大多数临床医生来说，“傅里叶”这个词意味着复杂的积分、晦涩的希腊字母，以及那种“我永远学不会这个”的挫败感。所以，我们选择了妥协。我们死记硬背：“球差导致光晕”、“慧差导致拖尾”。我们记住了结论，却失去了直觉。

但理查德·费曼 (Richard Feynman) 曾说过一句震耳欲聋的话：

“你要理解，不要死记硬背。要学习原理，而不是公式。”

(Understand. Don't memorize. Learn principles, not formulas.)

这本书，就是为了帮你跨越这道鸿沟而写的。

这不是一本教科书，这是一个“云端实验室”

如果不使用一个数学公式，能否学会傅里叶光学？在十年前，这也许是不可能的。但今天，感谢计算科学的进步，我们可以换一种方式学习。

这本书的核心理念非常简单：代码即玩具 (Code-as-Toy)。

在这本书里，我们不会让你推导公式。相反，我们将利用 Wolfram Cloud 这一强大的云端工具，把枯燥的数学公式变成可以把玩的“光学玩具”。

• 你不需要是程序员。
• 你不需要在电脑上安装任何软件。
• 你只需要一个浏览器。

在这个“云端实验室”里，你将不再是被动的阅读者，而是主动的探索者：

• 在第 7 章，你不再是盯着静态的 Zernike 金字塔发呆。你将亲手拖动滑块，看着一个完美的波前如何被你“捏”成“碗状”（近视）或“马鞍状”（散光）。
• 在第 8 章，你将亲自把这些像差“卷积”到一个视力表上。你将亲眼看到那个完美的“E”字，是如何因为你增加了一点点“彗差”而长出了拖尾。那一刻，你会惊呼：“啊！这就是我病人描述的那个画面！”
• 在第 12 章，你甚至会像建筑师搭积木一样，利用“包络线原理”亲手设计一款三焦 IOL，并理解为什么厂商要把第二个焦点设在 +1.5D。

我们的承诺

当你读完这本书时，我不希望你成为一名数学家。但我希望，下一次当你坐在诊室里，面对那位抱怨眩光的 LASIK 患者时，你不再需要苍白地解释术语。

你可以自信地打开浏览器，点击收藏夹里的链接，把屏幕转向病人，说道：

“来，让我们一起看看你的眼睛里发生了什么。你看，当我移动这个‘球差’滑块时，屏幕上的车灯是不是也变样了？这就是物理学告诉我们的故事。”

从今天起，让我们停止背诵，开始看见。

准备好了吗？让我们打开那个黑箱。

⚠️ 法律免责声明

请在开始阅读前仔细阅读以下内容：

本书提供的所有 Wolfram Cloud 代码、交互式模拟及可视化结果，仅用于教育演示、原理理解与教学目的。

• 非医疗器械：书中的光学模型均为理想化的物理模型，未包含生物力学响应、个体伤口愈合差异及复杂的神经适应过程。它们严禁直接用于临床诊断、手术参数设定、IOL 度数计算或作为任何医疗器械的替代品。
• 临床决策：所有临床决策必须基于经认证的医疗设备测量结果及医生的独立专业判断。作者及出版方不对基于本书代码进行的任何临床操作产生的后果承担法律责任。

如何使用本书：

全书每一章都配有专属的 Wolfram Cloud 代码。请务必在阅读时，将电脑或平板置于手边。

这不是阅读，这是一次实验。

第一部分：新语言的建立——工具与物理直觉

第 1 章：你的“云端超级计算器”

致 Dr. X：

让我们诚实地面对那一刻。

也许是上周二的晚上，还在上中学的孩子拿着作业本走进书房，指着一道一元二次方程 $ax^2 + bx + c = 0$ 问你：“爸/妈，这个 $x$ 到底怎么解？”

你盯着那行公式，脑海中隐约浮现出几十年前的高中数学老师，还有一个叫“韦达定理”还是“求根公式”的东西…… $\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$？还是 $4ac - b^2$？

在那一刻，作为一名能熟练操作飞秒激光、在微米级误差范围内重塑角膜的眼科专家，你犹豫了。

别担心，这正是我们要开始的地方。

这一章不是为了教你数学，而是为了给你一件武器。有了它，你不仅能秒杀孩子的数学作业，更能获得一把打开现代光学大门的万能钥匙。更重要的是，它能帮你完成那些你在手术室里瞬间需要的计算，而无需推导任何公式。

准备好了吗？我们要去云端了。

忘记“编程”，这是你的“数字手术台”

提到“代码”，你的第一反应可能是黑色的屏幕和无穷无尽的 Error。请把这些刻板印象统统扔进医疗废弃物垃圾桶。

我们将要使用的 Wolfram Cloud，请把它想象成一张“活的处方纸”。

• 你写下一个想法（比如一个光学术语）。
• 它立刻显影给你看。
• 零安装：只要有浏览器，你就能随时随地使用它。

[行动 1] 进入实验室

1. 打开浏览器，访问 http://www.wolframcloud.com。
2. 点击 "Sign Up for Free"（基础账户完全免费）。
3. 点击 "New Notebook"（新建笔记本）。

现在，你面前是一张空白的白纸。这就是我们的实验室。

五句“咒语”走天下

Wolfram 语言有 6000 多个函数，但作为眼科医生，你只需要掌握 5 个。

咒语一：计算——无穷的精度

在笔记本的第一个格子里输入：

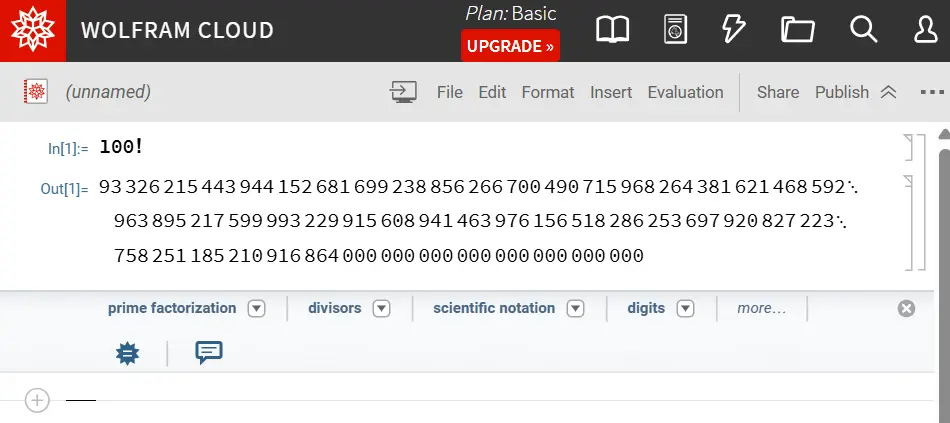
100!

然后，这是最关键的一步：按住 Shift 键，同时按 Enter 键（Shift + Enter）。

注意：单纯按 Enter 只是换行，Shift + Enter 才是“执行操作”（就像踩下显微镜的脚踏开关）。

屏幕上会瞬间出现一个长达 158 位的数字。它不会像 Excel 那样给你一个科学计数法的近似值，它给出的是绝对精确的真理。在光学计算中，这种精度至关重要。

咒语二：求解——你的代数外包团队

回到那个让孩子头疼的方程。你不需要背公式，你只需要告诉云端你的“意图”。

输入：

Solve[a * x^2 + b * x + c == 0, x]

(注意：函数名首字母大写；方程的等号要写两个 ==)

Shift + Enter。看，它直接吐出了那个标准的求根公式。

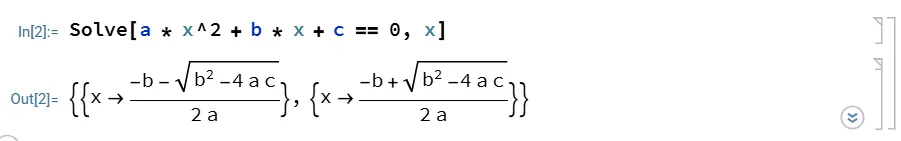
但这对你的临床工作有什么用？大有用处。

让我们看一个真实的临床场景：你需要根据角膜的折射率 ($n$) 和曲率半径 ($r$) 来计算屈光度 ($D$)，或者反过来。公式是 $D = \frac{n-1}{r}$。

如果你想知道 $r$ 怎么算，不需要自己在纸上移项变号。

输入：

Solve[D == (n - 1) / r, r]

Shift + Enter。

输出： $\left\{ \left\{ r \to \frac{-1+n}{D} \right\} \right\}$

看，它告诉你：$r$ 等于 $(n-1)$ 除以 $D$。这不仅仅是计算器，这是你的数字手术刀——你告诉它“我要切哪里”（求解 r），它自动规划路径。

咒语三：替换——这种思维叫“开处方”

这就引出了 Wolfram 语言中最像医生思维的一个符号：/. （替换规则）。

想一想，教科书上的公式 $D = \frac{n-1}{r}$ 是通用的治疗指南。

但当你面对具体的病人——比如张先生，角膜折射率 $n=1.3375$，曲率半径 $r=7.8mm$ (0.0078m)——你需要把指南变成针对该病人的处方。

在 Wolfram 里，我们这样写：

(* 这是一个通用公式 *)
formula = (n - 1) / r

(* 这是一个针对特定病人的“处方” *)
formula /. {n -> 1.3375, r -> 0.0078}

Shift + Enter。

输出： 43.2692

解读：

• /. 的意思是“基于以下条件执行...”。
• -> 的意思是“取值为...”。
• 这行代码的医学含义是：“对于公式 A，当病人参数为 B 时，结果是多少？”

掌握了 /.，你就掌握了定制化 IOL 计算的核心逻辑。

咒语四与五：绘图与交互——你的数字裂隙灯

人类是视觉动物。光看公式 $y = x^2$ 很难有直观感受。让我们把它画出来。

输入：

Plot[x^2, {x, -2, 2}]

你会看到一条抛物线。

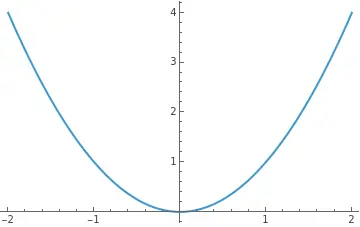
但作为眼科医生，我们更喜欢动态的观察。就像在裂隙灯下，你会推拉操纵杆来改变切面。在云端，这个操纵杆叫 Manipulate。

让我们把上面的抛物线变成一个可以把玩的“玩具”。请直接复制下面的代码，别被长度吓到，我们来看“医学翻译”：

(* 启动数字裂隙灯 (Manipulate) *)
Manipulate[

(* 1. 显影区域 (Show): 画出这个波前形状 *)
Plot[c * x^2, {x, -5, 5}, PlotRange -> {-10, 10}],

(* 2. 操纵杆 (Knobs): 设定变量 c 的调节范围 *)
{c, -2, 2}
]

Shift + Enter。

这就是你的“啊哈！”时刻。

屏幕上出现了一个滑块。

• 试着拖动 c。
• 当 c 变大，开口变小，曲线变陡。
• 当 c 变成负数，曲线翻转。

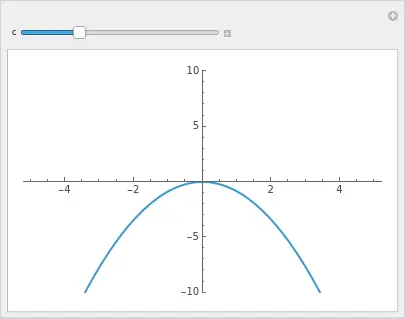
Dr. X，请停下来思考一秒钟。

刚才那个上下翻飞的抛物线？在光学里，它就是“离焦”。

• 当开口朝上，它是近视的波前（光线汇聚过早）。
• 当开口朝下，它是远视的波前。
• 当 c=0，它是一条直线，代表正视眼的平面波。

你没有在做数学题，你在“把玩”近视和远视的物理本质。

本章小结：你的工具箱

1. Wolfram Cloud：你的云端笔记本，无需安装。
2. Shift + Enter：你的“脚踏开关”，运行指令。
3. Solve：你的代数外包团队。
4. /. (替换)：你的“处方笔”，将通用公式应用于具体病人。
5. Manipulate：你的“数字裂隙灯”，将枯燥的公式变成可视化的直觉。

下章预告：

现在你已经熟悉了操作台。在下一章，我们将进行第一次真正的光学实验：我们将用代码“画”出一束光波，并亲眼看看“相位”到底是如何移动的。别眨眼，光要来了。

第 2 章：告别“黑箱”——你的第一个“光学”实验

致 Dr. X：

在上一章，我们用“云端计算器”解决了一元二次方程。那很有趣，但你的咖啡可能已经凉了，而你的心里或许还在嘀咕：

“这很好，但我是眼科医生。我关心的是怎么读懂那张色彩斑斓的波前像差图，怎么向 LASIK 术后的病人解释眩光，而不是在这里画抛物线。”

你完全正确。

在这个诊室里，每天都有无数光线穿过你病人的角膜、晶状体，最终落在视网膜上。有时候，它们完美汇聚（1.0 视力）；有时候，它们像脱缰的野马一样乱跑（眩光、彗差）。

作为医生，我们习惯了看机器吐出来的“结果”——那些地形图和 Zernike 金字塔。但我们很少去探究“源头”。

今天，我们要打破这个习惯。我们要抛弃死板的物理课本定义，做一件你在医学院从未做过的事：亲手“捏”一束光，然后让它跑起来。

我们将攻克那个在光学教科书里最抽象、却又是一切像差根源的概念——“相位” (Phase)。

准备好了吗？让我们开始你的第一个光学实验。

1. 光的“红细胞”：正弦波

如果我们要理解血液动力学，我们得先了解红细胞。同样，如果我们要理解复杂的眼科光学（无论是圆锥角膜的像差，还是 OCT 的干涉条纹），我们需要找到光的“红细胞”。

它就是正弦波 (Sine Wave)。

不管你病人眼里的像差有多复杂，也不管 OCT 扫描出的视网膜断层有多精细，它们本质上都是由无数个简单的正弦波“叠加”而成的。

所以，让我们先在云端“画”出这第一束光。

[实验 2.1] Hello, Light!

请点击下方的链接，或者在你的 Wolfram Notebook 中输入以下代码。

💡 提示：这和上一章画抛物线的咒语一模一样，只是我们把 $x^2$ 换成了 Sin[x]。

(* 模拟一束穿过完美晶状体的理想光波 *)
Plot[Sin[x], {x, 0, 4 Pi}]

(请按 Shift + Enter 运行)

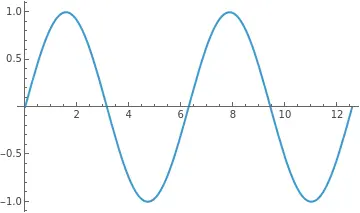
看！ 屏幕上出现了一条完美的波浪线。起伏、平滑、周期性。

这就是一束理想的光。想象一下，这束光正在穿过患者原本完美的屈光介质。在波动光学的语境下，波峰是光能量最强的地方，波谷是最弱的地方。

这很简单，对吧？但静态的光是没有生命的。接下来，我们要引入那个让无数医生头疼的概念。

2. 那个可怕的词：“相位” (Phase)

现在，请允许我做一个小小的测试。当你在学术会议上听到“相位”这个词时，你的脑海里浮现出了什么？

• A. 一个令人困惑的希腊字母 $\phi$。
• B. 一个复杂的三角函数公式 $\sin(\omega t + \phi)$。
• C. “这和我有什么关系？我只要知道 Zernike 系数就行了。”

如果你的答案是 A 或 B，那么恭喜你，你是传统物理教学的受害者。教科书会告诉你“相位是波在特定时刻循环中的位置”。这句解释不仅枯燥，而且完全无法转化为临床直觉。

在我们的实验室里，我们拒绝这种定义。我们要用“动起来”的方式来重新定义它。

还记得上一章的“数字裂隙灯” (Manipulate) 吗？现在，让我们把“相位”变成一个你可以亲手拖动的滑块。

[实验 2.2] 让光波“跑”起来

请仔细阅读下面这段代码。注意，我们采用了“医学翻译”风格的注释，因为我们不是在写程序，我们是在“开处方”。

(* 启动数字裂隙灯 (Manipulate) *)
Manipulate[

(* 1. 显影区域 (Show): 可视化视网膜前的光波路径 *)
Plot[Sin[x + p], {x, 0, 4 Pi}, 
 PlotRange -> {-1.5, 1.5}, 
 PlotLabel -> "这就是相位！"],

(* 2. 操纵杆 (Knobs): 注入“相位延迟” (Phase Delay) *)
(* 模拟光线经过不同厚度的角膜或晶状体时产生的滞后 *)
{p, 0, 2 Pi}
]

(请按 Shift + Enter 运行)

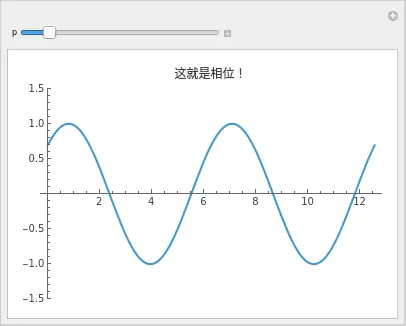
屏幕上出现了一个滑块。这是本书的第一个“啊哈！”时刻 (Aha! Moment)。

请把鼠标放在那个标记为 p 的滑块上。慢慢地、来回地拖动它。

看着屏幕上的那束波。发生了什么？

• 它在移动。
• 当你把滑块向右拖，波浪向左平移。
• 当你把滑块向左拖，波浪向右平移。

Dr. X，请停下来。看着屏幕。

你刚刚亲手操作的这个 p，在数学上就是“相位”。

你刚刚看到的波浪左右移动，在物理上就叫做“相移” (Phase Shift)。

这一刻，请把这个公式刻在脑子里：

在眼科光学中，相位 (Phase) = 位置 (Position)。

“改变相位”，就是把光波向前或向后“推”了一把。

3. 为什么这很重要？（你的第一个临床洞见）

你可能会说：“好吧，我知道相位就是平移了。但这和我的病人有什么关系？这和波前像差仪有什么关系？”

关系巨大。

想象一下，有两束光同时进入你病人的眼睛：

1. 光束 A：穿过角膜的中心。
2. 光束 B：穿过角膜的边缘。

如果病人的角膜是完美的（理想模型），这两束光会“齐步走”，它们的波峰和波峰是对齐的（相位相同）。

但是，如果病人有近视或者高阶球差呢？

边缘的那束光束 B 可能会穿过更厚的介质，或者路径更长。这就意味着，相对于中心的光束 A，光束 B “跑慢了”。

在物理上，这意味着光束 B 的“相位”发生了一个“平移”（就像你刚才拖动滑块一样）。

这就是“波前像差”的本质！

所谓的波前像差仪 (Aberrometer)，它测量的其实就是：眼睛瞳孔不同位置的光，相对于中心光线，到底被“平移”（推迟）了多少？

• 如果只是平移了一点点，它们还能聚焦。
• 如果平移得乱七八糟（相位差大），光线之间就会“打架”（干涉），病人就会在夜间看到车灯变成了炸开的烟花。

本章小结

1. 正弦波是光学的“红细胞”。
2. 在 Wolfram Cloud 里，Plot[Sin[x]] 就能帮我们看见光。
3. 最重要的一点：相位 (Phase) = 位置 (Position)。
4. 当你拖动滑块的那一刻，你已经战胜了物理学中最抽象的概念。你看到的不再是希腊字母，而是光波在空间中的移动。

下章预告：

只看一条线太不过瘾了。在第 3 章，我们要把这条线铺开，变成一张三维的“毯子”。我们将第一次看到那个神秘的“波前” (Wavefront)，并亲手用代码“捏”出近视和散光的形状。

做好准备，我们要升维了。

第 3 章：看不见的“地形图”：波前与干涉的魔法

致 Dr. X：

还记得上一章我们在屏幕上拖动的那条简单的正弦波吗？

当时我们得到了一个重要的结论：“相位 (Phase) 就是位置。”

这听起来很优雅，也很物理。但如果此时您正站在一台 WaveLight 或 VISX 准分子激光设备旁，手里拿着一份刚打印出来的“波前像差分析报告”，您可能会觉得我在欺骗您。

那张报告单上画着五颜六色的图：红色的山峰、蓝色的山谷、绿色的平原。它看起来根本不像一条波浪线，倒更像是一张复杂的地形图 (Topography)。

您不禁会问：“作者先生，您告诉我的正弦波去哪了？这上面画的到底是什么？是角膜的厚度？是曲率？还是某种我看不见的神奇能量？”

如果不搞懂这个问题，这台价值数百万的机器对我们来说就是一个画着漂亮图画的“黑箱”。

今天，我们要把上一章的那根“线”，编织成一张“面”。我们要去揭开那张彩色地形图的真面目——波前 (Wavefront)。

并且，我们将触碰光学的灵魂：当两束光相遇时，会发生什么？（剧透：这正是 OCT 能够“看穿”视网膜的秘密）。

1. 寻找“隐形”的连线

为了理解波前，让我们暂时离开诊室，去到水边。我们需要建立一个核心的视觉比喻：光波即水波。

场景 A：完美的点光源（比如一个星星）

想象您站在平静的湖边，往中心扔了一颗石子。

“咚”的一声，一圈圈圆形的涟漪向外扩散。

请按下时间的“暂停键”。

现在，拿一支笔，沿着最外面那一圈涟漪的最高点（波峰）画一条线。

您画出了一个完美的圆。这就是球面波 (Spherical Wave) 的波前。

场景 B：完美的远光源（平行光）

现在，想象您站在海边，看着远处涌来的海浪。

因为源头非常遥远（比如视力表的灯箱），当波浪到达您脚下时，它们不再是圆形的，而是一排排笔直、平行的长浪，像列队的士兵一样齐头并进。

再次暂停。如果您沿着这一排浪头的最高点画一条线。

您画出了一条完美的直线。这就是平面波 (Plane Wave) 的波前。

关键转折：当“直浪”遇到“透镜”

接下来发生的事情至关重要，请仔细看：

1. 入眼：当那一排排笔直的“平面波”（平行光）撞击到患者的角膜和晶状体时，中间的光走得慢（因为介质厚），边缘的光走得快（相对而言）。
2. 弯曲：于是，原本笔直的波浪线被“掰弯”了。
3. 正视眼 (Emmetropia)：在完美的眼睛里，光学系统会将这排直浪精确地弯曲成一个“汇聚的球面波”。它像一个完美的碗，向内收缩，最终所有的能量在一个点（焦点）同时撞击视网膜。

那为什么波前像差仪上，正视眼显示的是“平坦”的绿色呢？

因为像差仪显示的不是光的形状，而是光的错误 (aberration)。

机器在计算时，会拿一个“理想的参考球面” (Reference Sphere) 去和患者实际的波前做比较：

• 公式：实际波前 - 理想球面 = 波前像差 (Wavefront aberration)
• 正视眼：实际波前是完美的球面，减去理想球面，结果等于 0。
• 结论：所以在电脑屏幕上，完美的眼睛显示为一张平坦的纸（平面波前像差）。
• 有像差的眼睛：实际波前也是个球，但它表面坑坑洼洼（不规则散光）或者弯曲度不对（离焦）。一减去理想球面，剩下的就是那些凸起和凹陷——这就是我们在屏幕上看到的“地形图”。

2. 空间视角：亲手“扭曲”这张“差值图”

明白了这一点，我们就可以放心地操作 Wolfram Cloud 了。

请记住：我们在屏幕上画的，是去除了理想球面后的“像差地形图”。

[实验 3.1]：从“零误差”到“棱镜倾斜”

我们要画一个平面，代表波前像差为零（即光线完美汇聚）。

为了让您更有感觉，我在代码里加了一点纹理，请把这些线条想象成光波相对于理想状态的“抢跑”或“落后”。

请点击下方链接或直接输入代码：

（不需要读懂每一行，只需关注那些中文注释）

(* 启动 3D 波前像差演示器 *)
Manipulate[
Plot3D[tilt * x, {x, -2, 2}, {y, -2, 2},
 PlotRange -> {-2, 2},
 PlotLabel -> "波前像差图 (Wavefront Error Map)\n平面=完美汇聚",
 
 (* 视觉美化：模拟波前相位的等高线 *)
 Mesh -> {10, 0}, 
 MeshStyle -> Opacity[0.5],
 ColorFunction -> "Rainbow",
 Exclusions -> None
 ],

(* 操纵杆：控制波前像差的倾斜程度 *)
{{tilt, 0, "像差倾斜 (Tilt)"}, -1, 1, Appearance -> "Labeled"}
]

(Shift + Enter 运行)

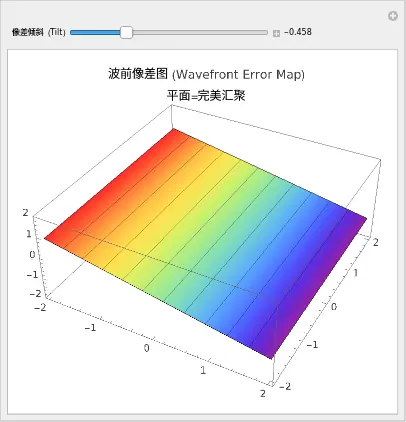
我们看到了什么？

当 tilt = 0 时，屏幕上是一张平整的彩色方块。

物理含义：这不是说光线在眼睛里是直的，而是说光线在眼睛里弯曲得非常完美，与理想球面零误差。

现在，动手时刻：

请拖动 tilt 滑块。

看！整张误差面倾斜了。

右边翘起来了，左边沉下去了。

这意味着什么？

这意味着实际的波前相对于理想的汇聚球面，发生了一个整体的角度偏差。

光线虽然汇聚了，但没有汇聚在视网膜中心（黄斑），而是偏到了旁边。

Dr. X，这就是“倾斜” (Tilt) 像差。

在 ANSI Z80.28 标准的 Zernike 金字塔里，它排在第 1 阶 ($Z_1^{-1}$ 或 $Z_1^1$)。这就像您在患者眼前加了一个棱镜 (Prism)。

恭喜您，您刚刚亲手模拟了光学中最简单的像差。在后面的第 7 章，我们将用同样的方法，在这个平坦的误差面上捏出“碗状”（离焦/近视：弯曲得太厉害了）和“草帽状”（球差：边缘弯曲得太多了）。

但现在，只需要记住：波前像差图，就是一张记录了“实际光波与理想汇聚光波之间差距”的地图。

3. 当光遇见光：干涉的魔法

理解了“波前”，我们只能算刚入门。要真正理解现代眼科设备（OCT、全息/衍射型 IOL），我们必须面对光波最诡异的“个性”——干涉 (Interference)。

在我们的直觉里，物质是“累加”的。

我给您一个苹果，再给您一个苹果，您就有了两个苹果。

我打开手电筒照亮墙壁，再打开一个手电筒，墙壁应该更亮，对吧？

错。

在光的世界里，1 + 1 并不总是等于 2。

有时候，1 + 1 = 0。

这就是干涉。

还记得那个正弦波吗？如果两个涟漪在水中相遇，会发生什么？

• 相长干涉 (Constructive)：如果它们的步调一致（波峰遇上波峰），它们会拥抱在一起，变成一个更高的巨浪。
• 相消干涉 (Destructive)：如果它们的步调刚好相反（波峰遇上波谷），这一波的波峰，刚好填平了那一波的波谷。水面瞬间变得风平浪静。

听起来很玄？让我们来做个实验，亲眼看看光是如何“自杀”的。

[实验 3.2]：让光“消失”的魔术

我们要画两个波（蓝色和橙色），然后画出它们叠加后的结果（红色）。

我们要拖动滑块，改变第二束光的相位（位置）。

输入代码：

(* 启动干涉演示器 *)
Manipulate[
Plot[{
  Sin[x],                 (* 蓝色：光波 A *)
  Sin[x + phase],         (* 橙色：光波 B (可变) *)
  Sin[x] + Sin[x + phase] (* 红色：叠加结果 *)
  }, {x, 0, 4 Pi},
 
 PlotStyle -> {Blue, Orange, {Red, Thickness[0.01]}},
 PlotRange -> {-2.5, 2.5},
 PlotLegends -> {"光波 A", "光波 B (可变)", "叠加结果 (A+B)"},
 PlotLabel -> "1 + 1 = ?"
 ],

(* 操纵杆：改变光波 B 的相位延迟 *)
{{phase, 0, "相位差 (Phase Diff)"}, 0, 2 Pi, Appearance -> "Labeled"}
]

(Shift + Enter 运行)

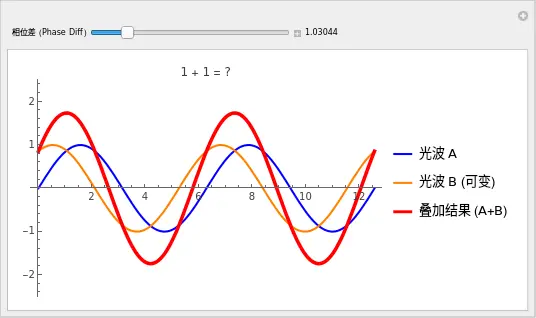
观察：

一开始 (phase = 0)：蓝色和橙色重合，红色的叠加波非常高大（1+1=2）。光很亮。

关键时刻：

慢慢拖动滑块，直到 phase 接近 3.14 (Pi)。

盯着那条粗红线。

它在变矮……变矮……

当 phase 变成 Pi 的一瞬间，红线变成了一条直线！

Dr. X，看着屏幕。光波 A 还在，光波 B 也还在，但它们叠加的结果是“零”。

这就是黑暗。

这就是为什么在某些特定角度下，肥皂泡会失去颜色；也是为什么在那昂贵的蔡司显微镜镜头上，那层蓝紫色的“抗反射镀膜”能消除反光——因为反射光被精心地“干涉”掉了。

4. 为什么这很重要？（OCT 的秘密）

您可能会想：“好吧，我可以把光变没。但这能帮我看病吗？”

能。而且这是眼科影像学的基石。

想象一下，您想测量眼底视网膜某一层只有 10 微米厚的结构。用尺子量？不可能。用超声波？精度不够。

这时候，我们请出干涉。

我们发射一束光到视网膜（信号光），同时发射另一束光到一面镜子上（参考光）。

当这两束光反射回来相遇时，只有当它们走过的路程几乎完全一样时，它们才会发生强烈的干涉（那个红色的高波峰）。

• 如果路程差了一点点？干涉就会减弱。
• 如果差多了？干涉就消失了。

OCT (光学相干断层扫描) 的本质，就是拿着一把“光的尺子”（参考臂），一点一点地去和眼底反射回来的光“对暗号”。

“嘿，这束光是在这里发生干涉了吗？”

“是的！那我这就记下来：这里有一层组织。”

这就是为什么 OCT 叫“光学相干 (Coherence) 断层扫描”。没有干涉，我们就是盲人。

(注：我们在第 10 章会详细拆解 OCT 如何利用傅里叶变换，从干涉条纹中算出深度，那将是另一个精彩的故事。)

本章小结

1. 波前 (Wavefront)：就是无数个光波波峰的连线。
2. 波前像差图：不要被“平坦”骗了。它不是说光线是直的，而是说实际波前与理想参考球面零误差。如果图是歪的，说明误差很大。
3. 干涉 (Interference)：光 + 光 = 黑暗（如果相位相反）。这是 OCT 和抗反射镀膜的物理原理。
4. 只有两张牌：无论光波多么复杂，它只有振幅（亮度）和相位（位置/形状）。波前像差仪之所以贵，是因为它捕捉到了相位。

下章预告：

既然光是一种波，那它通过我们那个小小的瞳孔时会发生什么？

为什么把瞳孔缩小可以看清东西（针孔效应），但缩得太小反而又看不清了？

下一章，我们将揭开“衍射” (Diffraction) 的面纱，并认识那个决定了人类视力极限的小圆斑——艾里斑。

请保持您的 Wolfram Notebook 打开，我们下章见。

第 4 章：“光圈”的诅咒与祝福——衍射与艾里斑

致 Dr. X：

还记得我们在门诊面对“难搞”的病人时，口袋里那个最简单的魔法道具吗？

当一位患者的视力怎么也矫正不上去，让你怀疑是不是有眼底病变时，你会给他递上一个 针孔片 (Pinhole)。如果他透过针孔能看清视力表，你会长舒一口气：“呼，看来视网膜没问题，只是我不小心搞错了屈光度。”

其中的道理你烂熟于心：针孔去除了像差，增加了焦深。

但是，Dr. X，在这个深夜的实验室里，我想请你进行一个极端的“思想实验”：

如果“小孔”能去除像差、提高视力，那我们为什么不干脆把孔做得极小？比如，给患者配一副只有 0.1mm 直径针孔的眼镜？那样岂不是能获得“无限”的焦深，彻底消灭老视，永远不需要调焦了吗？

如果你真的这么做了，你的病人会愤怒地告诉你：“医生，我的世界糊成了一团。”

这就引出了光学的终极悖论：缩小瞳孔（光圈）可以减少像差，但如果缩得太小，一种更底层的物理法则就会接管一切，摧毁清晰度。

这一章，我们要通过 Wolfram Cloud 亲眼看看这个物理学的“幽灵”——衍射 (Diffraction)。它是光学的物理极限，是为什么我们永远无法看清原子的原因，也是为什么老鹰的视力比我们好的秘密。

1. 光不喜欢被“囚禁”

我们在第 2 章学过，光是一种波。

想象一列整齐的士兵（平面波）正大步向前。突然，前方出现了一堵墙，墙上只有一个狭窄的门（瞳孔）。

当士兵们穿过这扇门时，会发生什么？

• 经典几何光学 会告诉你：士兵们穿过门后依然会走直线，形成一道边缘清晰、和门一样宽的光束。
• 波动光学（真实世界） 却告诉你：一旦波被“限制”在狭窄的空间里，它就会感到不安，开始向四周扩散。

这就是衍射。简单说：光圈越小，光越“不想”走直线，它扩散得越厉害。

这种扩散在视网膜上形成了一个特殊的同心圆图案：中心是一个明亮的圆斑，周围是一圈圈淡淡的光环（注意这些光环，它们是光的干涉条纹。请记住它们，在第 10 章我们将利用这种条纹的特性，让 OCT 机器“看穿”视网膜的断层结构）。

物理学家给这个光斑起了一个优雅的名字：艾里斑 (Airy Disk)。

别信我的描述。让我们在云端亲手“制造”一个。

[实验 4.1]：瞳孔越小，光斑越大？

我们要模拟一个点光源（比如远处的星星）成像在视网膜上的样子。我们要探究的是：当你在做手术或检查时，改变患者瞳孔大小，视网膜上的这个“点”到底变成了什么样？

请复制下方代码贴进wolfram notebook里。注意看注释，我们不说数学，只说医学。

(* 启动艾里斑模拟器 *)
Manipulate[
Module[{r},
 (* 定义光强分布公式 *)
 (* BesselJ 是描述圆形波纹扩散的数学函数，类似于水波的 Sin *)
 intensity[x_, y_, pupil_] := (2 * BesselJ[1, pupil * Sqrt[x^2 + y^2]] / (pupil * Sqrt[x^2 + y^2] + 10^-10))^2;

 (* 绘制视网膜上的图像 *)
 DensityPlot[intensity[x, y, pupilSize], {x, -10, 10}, {y, -10, 10},
  PlotRange -> All,
  ColorFunction -> "GrayTones", (* 模拟黑白视觉 *)
  PlotPoints -> 60,
  Frame -> False,
  PlotLabel -> Style["视网膜上的像 (Airy Disk)", 16, Black],
  Epilog -> {White, Text[Style["瞳孔直径模拟值: " <> ToString[pupilSize], 12], {0, 8}]}
 ]
],
(* 操纵杆：改变瞳孔大小 *)
{{pupilSize, 2.0, "瞳孔孔径 (Aperture)"}, 0.5, 5.0}
]

(Shift + Enter 运行)

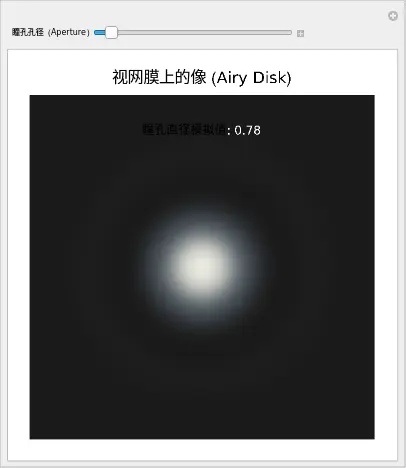
现在，请做那个违背直觉的操作：

1. 向右拖动滑块（增大瞳孔）：看！中心的亮斑变得很小、很锐利。光能量高度集中。
2. 向左拖动滑块（缩小瞳孔）：注意发生了什么？中心的亮斑反而变大、弥散了！周围的同心圆光环也变得更明显。

Dr. X 的洞见：

这就解释了那个悖论。人眼永远在两个敌人之间战斗：

• 针孔效应（几何光学）：瞳孔越小，像差越少，图像越清晰。
• 衍射效应（波动光学）：瞳孔越小，艾里斑越大，图像越模糊。

在人眼中，这两个效应一直在“拔河”。这也就是为什么人眼的最佳解析力瞳孔直径通常在 2.5mm - 3mm 左右。太大了有球差，太小了有衍射。

2. 瑞利判据：视力表的物理终点

现在你知道一个“点”在视网膜上其实是一个“斑”了。那如果我们在看视力表上的“E”字呢？

“E”字的开口，本质上就是两个相邻的“点”。

• 如果这两个点离得很远，它们对应的两个“艾里斑”也离得很远，你能清楚地看到是两个点（看清了开口）。
• 如果这两个点靠得太近，它们的“艾里斑”就会融合在一起，变成一个长条形的模糊斑点。你就分不开了（看不清开口）。

这就引出了光学中最重要的判据——瑞利判据 (Rayleigh Criterion)。

它规定了：当一个艾里斑的中心，刚好落在另一个艾里斑的第一道“暗环”上时，我们就认为这两个点“刚刚好”能分辨。

这听起来很抽象？没关系，我们让它动起来。

[实验 4.2]：决战视力表——瑞利判据演示

这段代码模拟了两个视标点（就像“E”字的两个笔画）。你可以通过滑块控制它们靠得有多近，看看你的眼睛什么时候会“瞎”。

(* 启动分辨率极限演示 *)
Manipulate[
Module[{d = separation / 2, i1, i2},
 (* 模拟左边光点的视网膜成像 *)
 i1[x_] := (2 * BesselJ[1, 3 * (x + d)] / (3 * (x + d) + 10^-10))^2;
 (* 模拟右边光点的视网膜成像 *)
 i2[x_] := (2 * BesselJ[1, 3 * (x - d)] / (3 * (x - d) + 10^-10))^2;

 (* 绘制光强剖面图 *)
 Plot[{i1[x], i2[x], i1[x] + i2[x]}, {x, -4, 4},
  PlotStyle -> {
    {Blue, Dashed, Thickness[0.005]}, (* 光点 A *)
    {Red, Dashed, Thickness[0.005]},  (* 光点 B *)
    {Black, Thick}                    (* 视网膜实际看到的总图像 *)
   },
  PlotRange -> {0, 2.2},
  Filling -> {3 -> 0}, (* 填充总光强下方的区域 *)
  PlotLabel -> Style[
    If[separation > 1.22, "状态: 清晰分辨 (Resolved)",
      If[separation > 0.9, "状态: 勉强分辨 (Rayleigh Limit)", "状态: 无法分辨 (Unresolved)"]],
     18, Red],
  ImageSize -> Large
 ]
],
(* 操纵杆：改变两点间距 *)
{{separation, 3.0, "两点间距"}, 0, 3.0}
]

(Shift + Enter 运行)

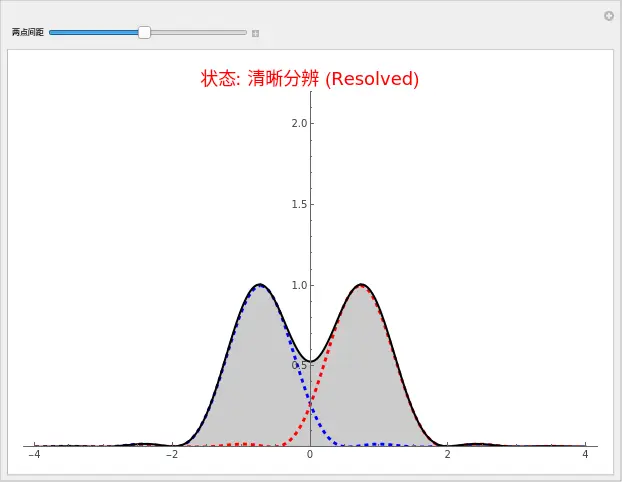
这是见证奇迹的时刻。屏幕上有三条线，请只盯着那条黑色的实线 —— 那是你的视网膜真正看到的东西。

请慢慢向左拖动滑块，减小间距：

1. 分离阶段（间距大）：黑色实线有两个明显的“驼峰”，中间有一个深谷。你的大脑毫无疑问地判断：“这是两个点。”（视力 1.0）
2. 瑞利极限（间距 ≈ 1.0）：注意看！两个驼峰之间的“深谷”变得很浅了，但依然能看到一点点凹陷（约 74% 的峰值高度）。这就是瑞利判据的临界点。在这个距离下，视力好的医生能勉强看出“好像是两个点”。
3. 无法分辨（间距极小）：继续向左拖。黑色的实线变成了一个单峰的大鼓包！中间的凹陷彻底消失了。此时，无论你怎么努力，无论你有没有配眼镜，你都只能看到一个模糊的大点。

这就是物理学为你划定的终点线。

3. 为什么老鹰的视力比我们好？

Dr. X，现在你掌握了这个强大的理论工具，我们就能回答一些有趣的生物学问题了。

瑞利判据的公式其实很简单：

其中 $\theta$ 是最小分辨角（视力），$\lambda$ 是光波长，$D$ 是瞳孔直径。

看这个公式的分母 $D$。瞳孔越大，分辨角 $\theta$ 越小（分辨能力越强）。

• 老鹰：它们的瞳孔相对头部的比例极大，衍射效应极小，艾里斑极小，所以能从几千米高空看到地上的老鼠。
• 我们：我们在 2.5mm 瞳孔下的衍射极限，大约对应 1 分（1 arcmin）的视角。这恰好就是视力表上 1.0 (20/20) 的定义。

人类进化的精妙之处在于：我们的视网膜细胞密度，刚好就匹配了这个衍射极限。再增加细胞密度也没用了，因为物理学限制了光斑不可能更小。

本章小结

1. 光不喜欢被限制：任何光圈都会产生衍射，把完美的“点”变成一圈圈的“艾里斑”。
2. 孔越小，斑越大：这就是为什么针孔眼镜不能做成无限小。
3. 瑞利判据：当两个艾里斑重叠到中间的凹陷消失时，我们就到了物理视力的极限。

下章预告：透镜的真面目

看着屏幕上那个同心圆状的艾里斑，你是否觉得它看起来有点眼熟？

如果我告诉你，这个由“物理衍射”产生的同心圆图案，在数学上，恰好就是那个圆形瞳孔的傅里叶变换 (Fourier Transform)，你会相信吗？

是的，透镜不仅仅是汇聚光线的玻璃，它本质上是一台光速运行的模拟计算机。它每时每刻都在进行傅里叶变换。

在下一章，我们将正式揭开傅里叶变换的面纱。别怕，我不讲公式，我为你准备了一个关于“声音”的绝妙比喻。

请保持你的 Wolfram Notebook 打开，我们下章见。