本章的Gemini动态视图演示： https://gemini.google.com/share/4a03b66f8886

第二部分：视觉的引擎——傅里叶光学的核心

第 5 章：傅里叶“魔术”(I)——像“听”交响乐一样“看”角膜

致 Dr. X：

请深呼吸。

我知道，当你在目录里看到“傅里叶变换”这五个字时，你的皮质醇水平可能升高了。在大多数光学书里，这一章通常是灾难现场：充满了积分符号 ∫\int、复数 e−iωte^{-i\omega t} 和令人费解的数学证明。那时候，大多数医生会选择合上书，去喝杯咖啡。

但我向你保证：今天我们不写公式，我们要去听一场音乐会。

请回想一下你诊室里的那台角膜地形图仪 (Corneal Topographer)。

当一个圆锥角膜或者是角膜移植术后的病人坐上去，打印出来的图是一团乱麻。对于规则散光，你很舒服，因为你可以用两个简单的数字描述它：K1, K2（曲率）。

但对于那种坑坑洼洼的不规则角膜，机器却吐出了一堆奇怪的指数：SRI (表面规则指数)、SAI (表面不对称指数)、CIM……

你有没有想过：机器到底是用什么语言，把那个像“月球表面”一样复杂的角膜，翻译成这些数字的？

它用的语言，就是傅里叶变换 (Fourier Transform)。

如果不理解它，我们后面的旅程——无论是理解像差、MTF，还是设计多焦晶体——都将寸步难行。所以，请给我十分钟。我们不仅要搞懂它，还要在云端亲手“玩”弄它。

1. 您的耳朵就是一台傅里叶计算机

在进入光学之前，我们先闭上眼睛。想象你正在听一场交响乐。

空气中震动着无数复杂的声波。大提琴的低鸣、小提琴的高亢、长笛的清脆……它们全部混合在一起，变成了一股极其复杂的空气压力波，撞击着你的鼓膜。

  • 在物理上，这是一团混乱的波形（我们称之为时域 Time Domain）。
  • 但在感觉上，你的耳朵和大脑做了一件神奇的事：你能瞬间听出：“哦，这是一个 C 大调和弦，由 Do (C)、Mi (E)、Sol (G) 组成。”

停！就在这一瞬间，你完成了一次傅里叶变换。

  • 输入：一个混合的、复杂的声波（原本的信号）。
  • 处理：分解。
  • 输出：一张“乐谱”（频率的列表）。

傅里叶变换的灵魂只有一句话：任何复杂的波，都可以被拆解为一系列简单正弦波 (Sine Waves) 的叠加。

这就是进化的秘密：哪怕是最复杂的噪音，也不过是无数个简单的正弦波叠在一起罢了。而傅里叶变换，就是那个拥有“绝对音感”的分解器。

用gemini做了一个炫酷的声学傅里叶变换演示： https://gemini.google.com/share/2dc3d04e0165

2. 空间频率：把“时间”变成“距离”

好了，睁开眼睛。让我们从“耳朵”切换回“眼睛”。

声波是在时间上振动（一秒钟震动多少次，Hz）。

角膜（或光波）是在空间上起伏（一毫米起伏多少次）。

如果我们把“时间频率”换成“空间频率” (Spatial Frequency)，奇迹就发生了。我们可以像听音乐一样“听”这幅图像：

  • 声音的“低音” (Bass) →\rightarrow 图像的“轮廓”（低空间频率）。
    • 临床对应：角膜的整体弧度、近视、远视。
  • 声音的“高音” (Treble) →\rightarrow 图像的“细节/边缘”（高空间频率）。
    • 临床对应：角膜上的小疤痕、LASIK 瓣的边缘、不规则的突起。

在眼科里，我们用 CPD (Cycles Per Degree，周/度) 来衡量空间频率。

  • 30 CPD ≈\approx Snellen 视力表上的 1.0 (20/20) 视标。这是“极高音”，代表锐利的细节。
  • 3 CPD ≈\approx Snellen 视力表上的 0.1 (20/200) 视标。这是“低音”，代表模糊的大轮廓。

所以，当你给白内障病人做手术时，你本质上是在努力恢复病人“听高音”（看清细节）的能力。

3. 实验 5.1：在云端“搭建”一个方波

“Dr. X，这听起来像个比喻。你真的能用圆滑的‘正弦波’，拼出一个有棱有角的‘方块’吗？”

绝大多数人都不信。直觉告诉我们：圆的就是圆的，方就是方的，水火不容。

别信直觉，信代码。

让我们在 Wolfram Cloud 里亲手做一个“光学乐高”实验。我们要用无数个圆滑的波，搭出一个锐利的方波。

请点击下方的链接，或者直接输入代码。请注意看注释，这不再是数学公式，而是我们构建角膜形状的“处方”。

(* 启动傅里叶积木工坊 *)
Manipulate[
 Module[{f},
  (* 1. 核心配方：定义如何用简单的正弦波叠加出复杂形状 *)
  (* n 是我们投入使用的“积木数量” *)
  f[x_, n_] := Sum[Sin[k*x]/k, {k, 1, n, 2}];


  (* 2. 显影区域：绘制角膜横截面 *)
  Plot[{
    (* 目标形状：我们想要模拟的完美方形切口 *)
    If[showTarget, Sign[Sin[x]] * Pi/4, Nothing],
    (* 实际形状：我们用正弦波“拼凑”出来的样子 *)
    f[x, terms]
    }, {x, 0, 4 Pi},


   (* 3. 视觉美化：让显示更像医学图表 *)
   PlotStyle -> {
     {Gray, Dashed, Thickness[0.005]}, (* 理想的手术切口（灰色虚线） *)
     {Blue, Thickness[0.008]}          (* 实际的波前形状（蓝色实线） *)
     },
   PlotRange -> {-1.5, 1.5},
   PlotLabel -> Style["傅里叶积木：用圆滑波搭建方波", 16, Black],
   ImageSize -> Large,
   Epilog -> {
     Text[Style["当前叠加层数: " <> ToString[terms], 14, Red], {6, 1.2}],
     Text[Style["包含的高频细节 (High Freq)", 12, Blue], {6, -1.2}]
     }
   ]
  ],
 (* 4. 操纵杆：增加高频成分 *)
 {{terms, 1, "正弦波数量 (谐波)"}, 1, 50, 2, Appearance -> "Labeled"},
 {{showTarget, True, "显示理想切口"}, {True, False}}
]

(请按 Shift + Enter 运行)

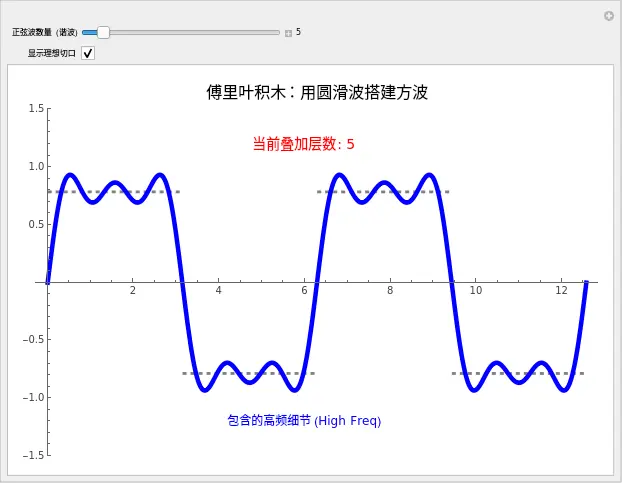
An image to describe post

动起来：见证魔术

现在，请把你的手放在 正弦波数量 这个滑块上。

  1. 初始状态 (terms = 1)：
    屏幕上只有一条蓝色的正弦波。它看起来很圆滑，完全不像背后的灰色方框。

    • 临床解读：这就像是一个只有“低音”的模糊视觉。你只能看到物体的大概位置，但看不清边缘。

  2. 开始搭建 (拖动滑块到 3)：
    看！波峰开始变平了，波谷也变平了。

    • 物理原理：我们加入了一个频率为 3 倍的“小波”。它像把手术刀一样，削平了主波的峰顶。

  3. 加速 (拖动滑块到 10)：
    蓝线开始紧紧贴合灰色的方框！虽然在转角处还有一些波纹（这叫吉布斯现象），但整体形状已经非常像“方形”了。

  4. 终极形态 (拖动滑块到 50)：
    Dr. X，看着屏幕。
    那条蓝线几乎变成了一个完美的方波。边缘锐利，转折 90 度。
    但请记住，它依然只是 50 个圆滑正弦波的叠加。

4. 洞见时刻 (The Aha! Moment)

这个实验揭示了角膜地形图仪的底层逻辑。

那台机器并不是在“画”角膜的每一个点。它是在做相反的事：它试图找出，需要叠加多少个不同频率的“正弦波曲面”，才能完美复现病人角膜的形状？

  • 如果只需要低频波 →\rightarrow 规则散光。
  • 如果需要大量高频波才能拼出来 →\rightarrow 不规则散光 (Irregular Astigmatism)。

那些让你头疼的 SRI, SAI, CIM 指数，本质上就是在那张“乐谱”上数一数：

“高音部（高频成分）的音量大不大？”

如果高音太多，说明角膜表面太粗糙，像差太大，视力质量 (MTF) 就会下降。

5. 为什么这很重要？

理解了“空间频率”，你就理解了视觉质量的一半。

  • 白内障就像是一个低通滤波器 (Low-pass filter)。它狠狠地砍掉了“高音”（高频细节），只留下了“低音”（模糊轮廓）。所以病人说：“我看得见门在哪里，但看不清门把手。”
  • LASIK 手术后的眩光往往来源于新引入的“高频噪声”（由切削边缘或高阶像差引起）。

在下一章，我们将见证更神奇的一幕：

既然我们可以用数学把光波“分解”成频率，那么有没有一种物理元件，能自动完成这个复杂的计算？

有的。它就在你的眼眶里。

透镜（晶状体），就是一台天然的傅里叶计算机。

请保持 Notebook 打开，Dr. X。下一章，我们要去看透镜是如何“计算”光的。

第 6 章：傅里叶“魔术”(II)——“透镜”就是傅里叶变换器

致 Dr. X：

上一章结束时，当我们终于把复杂的角膜形状拆解成了一堆正弦波频率时，我猜您可能正盯着天花板，手里转着咖啡杯，心里想着：“这太疯狂了。”

我们说：“要想理解角膜地形图，你必须先把角膜看作一张‘乐谱’（频谱），算出上面有多少低音（大轮廓）和高音（细节）。”

您可能会反驳：“作者先生，这只是数学游戏。为了看清视力表上的‘E’，我的视网膜和大脑难道每毫秒都在解几百万个微积分方程吗？人体里真的藏着一台超级计算机吗？”

答案既是“不”，也是“是”。

“不”，因为您的大脑不需要动笔算这些。

“是”，因为大自然确实在您的眼眶里塞进了一台光速运行的“模拟计算机”。

它就是您的晶状体（以及角膜）。

在这一章，我们要把第 4 章的“物理衍射”和第 5 章的“数学频谱”撞击在一起。我们将揭示光学中最令人起鸡皮疙瘩的秘密：透镜，不仅仅是汇聚光线的玻璃；它是在物理世界中，瞬间执行“傅里叶变换”的机器。

还记得第 4 章那个让您困惑的“艾里斑”吗？准备好，我们现在要揭开它的真实身份了。

1. 透镜的隐藏职业：角度“分类器”

我们在医学院学光路图时，教授通常这样画：

  • 平行光射入透镜 →\rightarrow 汇聚于焦点。

这句话是对的，但它漏掉了最精彩的部分。为了理解傅里叶光学，我们需要给透镜换个工作描述——把它看作一个 “角度分类器” (Angle Sorter)。

想象一下，有一堆乱七八糟的光线射向您的眼睛：

  • 光束 A：笔直射入（入射角 0°）。透镜把它抓过来，扔到了视网膜的正中心（黄斑中心凹）。
  • 光束 B：从上方斜着射入（入射角 10°）。透镜把它抓过来，扔到了视网膜的下方。
  • 光束 C：从更上方斜着射入（入射角 20°）。透镜把它扔到了视网膜的更下方。

发现了吗？透镜做了一件极其优雅的事：它把“角度”，转化成了“位置”。

所有相同角度的光，无论它们打在角膜的哪个部位，最终都会被汇聚到焦平面的同一个点。

不同的点，代表了不同的入射角度。

2. 为什么“角度”就是“频率”？

“好吧，”您说，“透镜能把不同角度的光分开，这像个棱镜。但这和傅里叶变换（频率）有什么关系？”

Dr. X，请回想一下第 3 章的海浪，以及第 4 章的衍射。

  • 低频信息（大轮廓）：就像平缓的波浪。光线在经过大轮廓时，折射/衍射的角度很小。
    • 结果 →\rightarrow 小角度 →\rightarrow 汇聚在视网膜中心。
  • 高频信息（锐利细节）：就像陡峭的波浪或狭窄的缝隙。为了“勾勒”出锐利的边缘，光线必须发生剧烈的衍射，产生很大的角度（还记得第 4 章吗？孔越小，光越扩散）。
    • 结果 →\rightarrow 大角度 →\rightarrow 汇聚在视网膜周边。

这就是著名的 “傅里叶光学原理”：

透镜后焦面（视网膜）上的光分布，就是前焦面（物体）的“傅里叶变换频谱”。

不需要电，不需要代码，不需要等待。光速穿过，计算完成。

视网膜中心记录的是“低频”（图像大概长什么样），周边记录的是“高频”（图像的细节边缘）。

3. 实验 6.1：眼见为实——圆孔的“幽灵”

我知道这听起来像天方夜谭。除非我们能亲眼看到它。

还记得第 4 章里，当我们缩小瞳孔时，那个讨厌的同心圆光斑——艾里斑 (Airy Disk) 吗？当时我说它是“衍射”的产物。

现在，我们要用第 5 章的数学工具（傅里叶变换），对一个“圆孔”做一次纯粹的数学运算。

如果我的理论是对的，那么这个“数学计算的结果”，应该和我们在第 4 章看到的“物理衍射的艾里斑”，长得一模一样。

请复制粘贴下面代码到您的 Notebook 中运行这段代码。

(注意：请仔细阅读代码里的注释，我把它们从“程序员语”翻译成了“眼科医生语”。)

(* 启动“透镜即计算机”演示 *)
Manipulate[
Module[{image, ft, logSpectrum},
 
 (* 1. 制造一个“光圈” (空域 Input) *)
 (* 这是一个白色的圆，代表我们的圆形瞳孔 *)
 image = Image[Graphics[{White, Disk[]}, Background -> Black, PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}}], ImageSize -> 128];

 (* 2. 执行傅里叶变换 (模拟透镜聚焦) *)
 (* Fourier: 模拟光线穿过晶状体并传播到视网膜的过程 *)
 (* RotateRight: 校准光轴，让0度光线（直流分量）正好打在视网膜中心 *)
 ft = RotateRight[Fourier[ImageData[image]], {64, 64}];

 (* 3. 显示结果 (频域 Output) *)
 (* Abs: 计算视网膜上感光细胞接收到的光强（亮度） *)
 (* Log: 调整显示灵敏度，就像眼睛适应黑暗一样，让我们能看清微弱的衍射光环 *)
 logSpectrum = ImageAdjust[Image[Log[Abs[ft] + 10^-6]]];

 Column[{
   Style["第一步：输入 (你的瞳孔)", 16, Blue],
   image,
   Style["   ⬇️ 经过透镜 (傅里叶变换) ⬇️   ", 20, Bold],
   Style["第二步：输出 (视网膜上的频谱)", 16, Red],
   Image[logSpectrum, ImageSize -> 250],
   Style[If[showHint, "看着眼熟吗？\n这不就是第4章的‘艾里斑’吗！", ""], 14, Purple]
 }, Alignment -> Center]
], 
{{showHint, False, "揭晓谜底"}, {False, True}}
]

(请按 Shift + Enter 运行)

An image to describe post

见证奇迹的时刻：

  1. 看上面那张图：那是一个简单的白色圆圈。这是我们的“输入”——一个完美的圆形瞳孔。
  2. 看下面那张图：那是经过傅里叶变换后的“频谱”。
  3. 请勾选“揭晓谜底”。

Dr. X，您认出它了吗？

下面那个中心明亮、周围有一圈圈同心圆环的图案，正是我们在第 4 章费尽口舌讲的“艾里斑”！

这就是那个“啊哈！”时刻：

  • 第 4 章（物理）说：光通过圆孔发生衍射，形成艾里斑。
  • 第 6 章（数学）说：圆函数的傅里叶变换，是艾里斑（贝塞尔函数形式）。

结论：衍射 ≈\approx 傅里叶变换。

当光线穿过瞳孔射向视网膜时，它并不是在简单地“投射”影子。它是在进行一次精密的数学运算。视网膜上那个模糊的光斑，本质上就是瞳孔形状的傅里叶频谱。

4. 为什么这改变了一切？

理解了“透镜就是傅里叶变换器”，您就不再只是一个开刀的医生，您是一个光学黑客。

因为这意味着，如果我们想改变视网膜上的像（比如消除像差，或者制造多焦点），我们只需要在透镜前（瞳孔平面）“编辑”光线的相位。

  • 白内障：晶状体变得浑浊，就像在透镜里塞进了杂质，它破坏了高频信息的传递（高频截止），所以病人觉得“蒙了一层纱”，看不清细节。
  • 多焦 IOL：我们在晶体表面刻上一圈圈的台阶（衍射光栅）。这实际上是在强行“篡改”傅里叶变换的过程，把原本应该汇聚在一个点（单焦）的能量，强制分配到两个点（远、近）上。

Dr. X，您现在手里已经拿到了打开“波前像差”大门的钥匙。

在这之前，像差只是纸上几个抽象的 Zernike 系数（Z40,Z31...Z_4^0, Z_3^1...）。

但现在，我们知道它们是如何干涉这场“傅里叶变换”的。

下一章，我们要玩个大的。

我们要把第 7 章变成一个 “像差模拟器”。我们要输入那些让您头疼的 Zernike 系数，然后亲眼看看它们是如何把完美的“艾里斑”，扭曲成病人抱怨的“彗星（彗差）”、“光晕（球差）”和“鬼影”的。

请保持您的 Wolfram Cloud 打开。真正的临床实战，才刚刚开始。

本章小结

  1. 透镜是计算机：它能瞬间完成二维傅里叶变换，无需电力。
  2. 角度 = 频率：透镜把不同角度入射的光（空间频率），映射到焦平面上不同的位置。
  3. 物理与数学的统一：物理上的“夫琅禾费衍射图样”，在数学上就是“光圈函数的傅里叶变换”。
  4. 艾里斑的本质：它就是“圆形”这个几何形状在频域的样子。

下章预告：

第 7 章：[镇书之章] 波前像差——“复现”患者的眩光

我们将引入 ANSI Z80.28 标准的 Zernike 多项式（我们的“乐高积木”），亲手毁掉一个完美的波前，看看会发生什么。

第 7 章：[镇书之章] 波前像差——“复现”患者的眩光

致 Dr. X：

这是一个典型的周二下午。

你刚做完一台堪称完美的 LASIK 手术。角膜瓣平整如镜，切削中心精准对位，术后第一天的电脑验光单上印着令人舒适的字样：平光 (Plano)，裸眼视力 1.2 (20/16)。

按理说，这该是击掌庆祝的时刻。但你的病人坐在裂隙灯前，表情却并不像个胜利者。

“医生，”他犹豫着说，“白天确实很清楚。但一到了晚上，所有的路灯都像‘炸开’了一样，周围有一圈雾。对面开过来的车灯甚至拖着尾巴，像彗星一样。我根本不敢开车。”

你皱起眉头，安排他去做了波前像差检查 (Wavefront Aberrometry)。机器吐出一张花花绿绿的地形图，旁边列着一串像天书一样的数字：

  • RMS: 0.45μm0.45 \mu m
  • Z20Z_2^0: +0.01+0.01
  • Z40Z_4^0: +0.25+0.25
  • Z31Z_3^1: −0.15-0.15

如果是五年前，你可能会盯着这些数字感到一阵眩晕：验光单明明是平光，为什么这里的数字还在跳动？那个 Z40Z_4^0 到底长什么样？为什么它会让路灯“炸开”？

欢迎来到第 7 章。在这里，我们要打破数学和临床的壁垒。我们要把这些冷冰冰的数字，翻译成你能看得见、摸得着的“物理形状”。

我们要揭开波前像差的本质：它不是魔法，它是光学的“乐高积木”。

1. Zernike 多项式：光的“乐高积木”

Dr. X，还记得我们在第 3 章建立的“波前”直觉吗？

  • 完美视力：波前像平静的湖面（平面波）。
  • 近视/散光：波前变得弯曲了。

现实中的角膜——尤其是经过屈光手术或有圆锥角膜风险的——其表面极其复杂，像起伏的山峦。如果你想向另一位医生描述这个复杂的形状，该怎么说？“嗯，中间有个坑，左边有点鼓，右下角稍微有点塌……”？这太不精确了，没法用于临床交流。

物理学家弗里茨·泽尼克 (Frits Zernike) 为我们提供了一套绝妙的语言。既然复杂的形状难以描述，那我们不如把它拆解成一堆标准的“基础形状”的叠加。

想象一下，你在玩乐高。你搭建了一个复杂的“城堡”（患者的波前）。虽然城堡看起来独一无二，但它其实只是由几种标准化的积木块拼成的：

  • 你用了 5 块“2x2 方砖”。
  • 你用了 3 块“1x4 长条”。
  • 你用了 1 块“斜坡砖”。

Zernike 多项式，就是眼科光学的“标准乐高积木”。

那张像差检查单上的数字（系数），就是这张“零件清单”。系数的大小（比如 0.25μm0.25 \mu m），只是告诉你：在这个病人的眼睛里，用了多少块这种形状的积木。

[重要标准] 为什么我们要用双索引 (n,mn, m)？

在我们开始玩积木之前，必须解决一个困扰眼科界多年的“巴别塔”问题。Zernike 多项式在物理界有多种排序标准（如 Noll 序列、Fringe/Zemax 标准）。作为眼科医生，我们必须严格遵守 ANSI/OSA Z80.28 标准。

这就是为什么我们在书中坚持使用双索引 ZnmZ_n^m：

  • nn (径向阶数)：代表积木的“复杂程度”。nn 越小，形状越简单（如近视）；nn 越大，形状越复杂（如多波峰的像差）。
  • mm (方位频率)：代表积木的“方向”和“形状特征”。

2. 认识“罪魁祸首”：四大金刚

有些积木是用来搭建地基的（低阶），有些是用来装饰塔尖的（高阶）。

低阶像差 (Lower Order Aberrations, LOA)

这两块积木你最熟悉，它们占据了人眼像差的 85% 以上。普通的框架眼镜和传统的激光手术，就是在处理它们。

  1. 离焦 (Defocus, Z20Z_2^0)
    • 形状：一个完美的“碗”。
    • 临床含义：近视（碗底朝下）或远视（碗口朝上）。
    • 后果：全图模糊，不挑形状。
  2. 散光 (Astigmatism, Z22Z_2^2)
    • 形状：一个“马鞍” (Saddle)。一个方向翘起，垂直方向凹陷。
    • 后果：物体变形，或者出现单向的重影。

高阶像差 (Higher Order Aberrations, HOA)

这才是本章的主角。它们通常很微小（只占 10-15%），但在夜间瞳孔放大时，它们是视觉质量的“刺客”。框架眼镜对此无能为力。

  1. 球差 (Spherical Aberration, Z40Z_4^0)
    • 形状：像一个墨西哥草帽 (Sombrero) 或者甜甜圈。中心是平坦的，但边缘剧烈翘起。
    • 临床场景：这就是那个 LASIK 术后抱怨“路灯炸开”的元凶！也是老花眼和夜间近视的成因。
    • 视觉感受：光晕 (Halo)。点光源周围包裹着一圈雾蒙蒙的光。
  2. 彗差 (Coma, Z31Z_3^1)
    • 形状：像一个被风吹歪了的帐篷，或者一个滑梯。一边高，一边低。
    • 临床场景：圆锥角膜 (KC) 的标志性像差！也是人工晶体偏位 (IOL Tilt/Decentration) 的特征。
    • 视觉感受：拖尾 (Comet Tail)。路灯像彗星一样拖着长长的尾巴。

3. 实验 7.1：Zernike 交互式仪表盘

说的再多，不如亲眼看一看。

Dr. X，我们现在把你的浏览器变成一台价值 5 万美元的波前像差分析仪。在这个实验中，我为你准备了一个“平坦”的完美波前。你的任务是作为一名光学工程师，拖动滑块（添加积木），看看这些数学名词到底对应什么样的物理形状。

请点击下方的 Wolfram Cloud 链接，或直接运行代码。请注意阅读注释，我特意用眼科术语翻译了代码逻辑。

[交互式实验] Dr. X 的波前像差模拟器

(* 启动波前像差模拟器 *)
Manipulate[
 (* 1. 建立角膜地形图模型 (Module 相当于建立一间独立的检查室) *)
 Module[{r, theta, zDefocus, zAstigmatism, zComa, zSpherical, wavefront},
  
  (* 设定视网膜坐标系：将直角坐标(x,y)转化为极坐标(r,theta)，符合眼科习惯 *)
  r = Sqrt[x^2 + y^2];
  theta = ArcTan[x, y];


  (* 2. 定义“乐高积木” (严格遵循 ANSI Z80.28 标准归一化公式) *)
  
  (* Z(2,0) 离焦: 这是一个完美的抛物面“碗”，模拟近视/远视 *)
  zDefocus = cDefocus * Sqrt[3] * (2 r^2 - 1);


  (* Z(2,2) 散光: 这是一个“马鞍”，模拟规则散光 *)
  zAstigmatism = cAstigmatism * Sqrt[6] * r^2 * Cos[2 theta];


  (* Z(3,1) 彗差: 这是一个“歪帐篷”，模拟圆锥角膜或晶体偏位 *)
  zComa = cComa * Sqrt[8] * (3 r^3 - 2 r) * Cos[theta];


  (* Z(4,0) 球差: 这是一个“墨西哥草帽”，模拟术后眩光 *)
  zSpherical = cSpherical * Sqrt[5] * (6 r^4 - 6 r^2 + 1);


  (* 3. 组合积木：将所有像差叠加，形成最终的波前形状 *)
  wavefront = zDefocus + zAstigmatism + zComa + zSpherical;


  (* 4. 可视化输出：绘制 3D 地形图 *)
  Plot3D[wavefront, {x, -1.2, 1.2}, {y, -1.2, 1.2},
   
   (* 模拟瞳孔遮挡：只显示直径范围内的数据 *)
   RegionFunction -> Function[{x, y, z}, x^2 + y^2 <= 1],
   
   (* 视觉美化：使用彩虹色谱模拟地形图仪的显示效果 *)
   ColorFunction -> "Rainbow",
   PlotRange -> {-2, 2}, (* 固定显示范围，避免画面抖动 *)
   Boxed -> False, Axes -> False, Mesh -> None,
   Lighting -> "Neutral",
   ImageSize -> {400, 400},
   PlotLabel -> Style["患者波前像差地形图 (Wavefront Map)", 16, Bold, RGBColor[0, 0.2, 0.6]]
  ]
 ],


 (* 控制面板：这里是你的“光学处方台” *)
 Style["低阶像差 (基础屈光不正)", Bold, 12],
 {{cDefocus, 0, "离焦 Z(2,0) [近视/远视]"}, -0.5, 0.5, Appearance -> "Labeled"},
 {{cAstigmatism, 0, "散光 Z(2,2) [规则散光]"}, -0.5, 0.5, Appearance -> "Labeled"},
 
 Delimiter, (* 分割线 *)
 
 Style["高阶像差 (夜间视觉杀手)", Bold, 12, Red],
 {{cComa, 0, "彗差 Z(3,1) [拖尾/偏心]"}, -0.5, 0.5, Appearance -> "Labeled"},
 {{cSpherical, 0, "球差 Z(4,0) [光晕/Halo]"}, -0.5, 0.5, Appearance -> "Labeled"},
 
 ControlPlacement -> Left
]

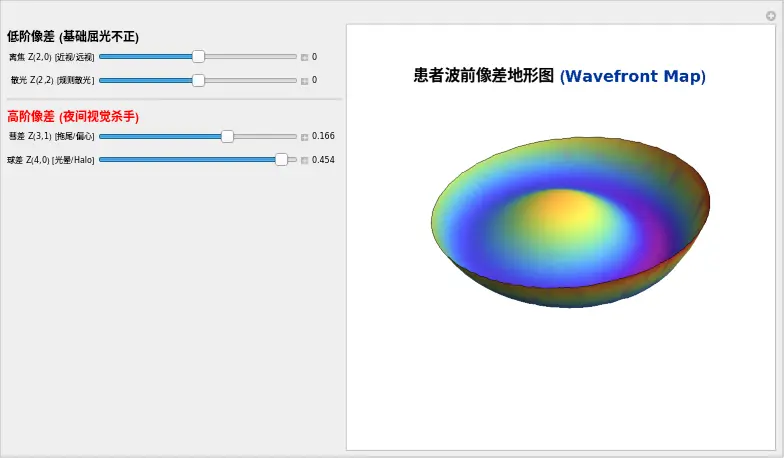
An image to describe post

见证“积木”的魔法：

  1. 归零（理想状态）：
    • 将所有滑块归零。看着那个彩色的平面。那是平光。像平静的湖面。这就是你的患者在白天（瞳孔缩小时）感受到的 1.2 视力状态。
  2. 制造“马鞍”（散光）：
    • 拖动 "散光 Z(2,2)" 滑块。
    • 注意看，它在一个方向上翘起（红色），在垂直方向上凹陷（紫色）。这意味着光线无法汇聚成一点，而是变成了两条焦线。这就是为什么散光患者眼里的月亮是重影的。
  3. 复现“夜间眩光”（球差）：
    • 现在，让我们模拟你那位不开心的 LASIK 病人。
    • 慢慢增加 "球差 Z(4,0)" 滑块。
    • 仔细看边缘！ 中心的区域（绿色/黄色）其实相对平坦——这解释了为什么他白天视力很好。但越往边缘（代表夜间瞳孔放大），波前翘起得越剧烈（深红色）。
    • 这就像一个帽沿高高翘起的“草帽”。当夜晚来临，瞳孔放大，光线穿过这些陡峭的边缘，被错误地折射，在视网膜上形成光晕。
  4. 复现“圆锥角膜”（彗差）：
    • 拖动 "彗差 Z(3,1)" 滑块。
    • 看那个形状，一边高耸入云，一边深陷谷底。这代表光路系统的极端不对称。这种像差极其致命，它会让点光源变成扫把星。

4. 洞见：解读 RMS (Root Mean Square)

现在回到那张让人生畏的检查单。除了 ZZ 系数，还有一个总分：RMS (均方根值)。

有了“积木”的概念，RMS 就不再是一个抽象的统计学术语了：它就是所有这些积木加起来的“总体积”或者“总重量”。

  • 它代表了波前偏离完美平面的“平均程度”。
  • RMS 越高，用来搭建这个波前的“捣乱积木”就越多，视觉质量通常越差。
  • 参考标准：通常 RMS < 0.1μm0.1 \mu m (对于 6mm 瞳孔) 是理想光学系统的及格线。你那位病人的 0.45μm0.45 \mu m 显然严重超标，尽管他的离焦（近视）是 0。

5. 为什么这改变了你的临床思维？

Dr. X，通过这一章，我们完成了一次从“看数字”到“看物理”的思维跃迁。

  • 当你下次看到 Z40Z_4^0 升高 时，你脑海中浮现的不应该是一个枯燥的定义，而应该是一个“中心平坦、边缘陡峭的墨西哥草帽”。
    • 你会立刻意识到：这个问题是瞳孔依赖的。
    • 你会对病人说：“你的眼睛像个广角镜头，白天中心成像很好，但晚上边缘进光时就会产生光晕。”
  • 当你看到 Z31Z_3^1 升高 时，你会想到那个“歪斜的滑梯”。
    • 你会立刻去检查晶状体是不是歪了 (IOL Tilt)，或者角膜地形图有没有圆锥样改变。
    • 你会对病人说：“你的眼睛把光线拖了个尾巴，像彗星一样。”

你不再是被机器数据轰炸的受害者，你是这些数据的翻译官。

预告：从“形状”到“模糊”

这一章，我们看清了光波扭曲的形状 (Wavefront)。

但作为一位严谨的医生，你可能会追问：“好的，我知道波前变成‘墨西哥草帽’了，但这到底为什么会让病人看到‘光晕’呢？波前的形状，到底是如何变成视网膜上的模糊图像的？”

问得好。这也是所有波前像差仪最核心的算法秘密。

连接“波前形状”（原因）和“视觉模糊”（结果）的桥梁，叫做 点扩散函数 (PSF)。

在下一章，我们将把这个“墨西哥草帽”扔进我们第 6 章搭建的“傅里叶变换机器”里，亲眼看看它是如何把一个完美的星点，炸成一团雾气的。

准备好了吗？我们要去“制造”一些模糊了。