为了分析方便,我们先将之前的计算整合成一个分段函数:
OrthoK[x_]=Piecewise[
{
{z[BCR, 0, 2 * x, 0], 0 <= x < BCD / 2},
{RCresult[[1, 2]]* x+RCresult[[2, 2]], BCD / 2 <= x < RCD / 2},
{z[ACresult[[1, 2]], 0, 2 * x, ACresult[[2, 2]]], RCD / 2 <= x < ACD / 2},
{z[PCresult[[1, 2]], 0, 2 * x, PCresult[[2, 2]]], ACD / 2 <= x < PCD / 2}
}
]
类似的,我们也可以写一个角膜表面矢高函数:
Eye[Reye_,Qeye_,x_]:=z[Reye,Qeye,2*x,0]
那么角膜表面和塑形镜后表面的矢高差,就是泪液层的厚度了,可以绘制出一张图像来
Plot[Eye[Reye,Qeye,x]-OrthoK[x], {x,PCD/2}]
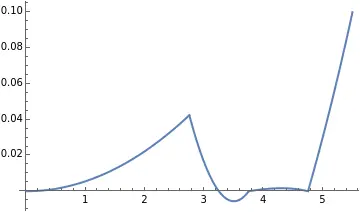
😓,有一点尴尬,穿模了,RC弧不能直接用一条直线连接BC弧末端和AC弧起点,中间会被角膜挡住一部分。
那么,我们其实可以练习一个稍微高阶一些的技巧——可以从泪液的厚度来反推RC弧需要的形态。比如我希望RC弧位置的泪液厚度保持恒定。
由于泪液厚度=Eye[Reye,Qeye,x]-OrthoK[x]
如果要求恒定,不希望有什么跳变,那么就应该等于泪液层在BC弧末端的泪液层厚度,也就是
OrthoK[x]= z[Reye,Qeye,2*x,0]+z[BCR,0,BCD,0]-z[Reye,Qeye,BCD,0]
得到的泪液厚度是这样的:
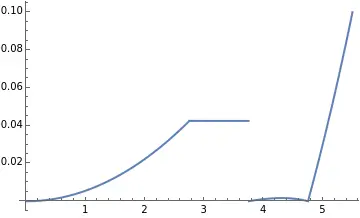
这么看连起了一端,另一端还是有跳变,也许会有不适,那么就硬来,让泪液层厚度逐渐减少到0。塞进一个线性减小的部分,
-(z[BCR,0,BCD,0]-z[Reye,Qeye,BCD,0])/(RCD/2-BCD/2)*(x-BCD/2)
于是塑形镜后表面的分段函数看起来是这样的:
OrthoK[x_]=Piecewise[
{
{z[BCR, 0, 2 * x, 0], 0 <= x < BCD / 2},
{z[Reye,Qeye,2*x,0]+z[BCR,0,BCD,0]-z[Reye,Qeye,BCD,0]-(z[BCR,0,BCD,0]-z[Reye,Qeye,BCD,0])/(RCD/2-BCD/2)*(x-BCD/2),
BCD / 2 <= x < RCD / 2},
{z[ACresult[[1, 2]], 0, 2 * x, ACresult[[2, 2]]], RCD / 2 <= x < ACD / 2},
{z[PCresult[[1, 2]], 0, 2 * x, PCresult[[2, 2]]], ACD / 2 <= x < PCD / 2}
}
]
泪液层厚度看起来是这样的:
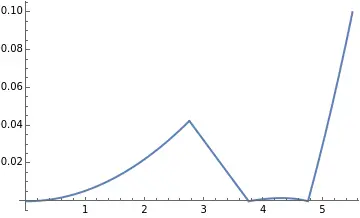
记住,这就是一个完美适配的角膜塑形镜的泪液层厚度形态。
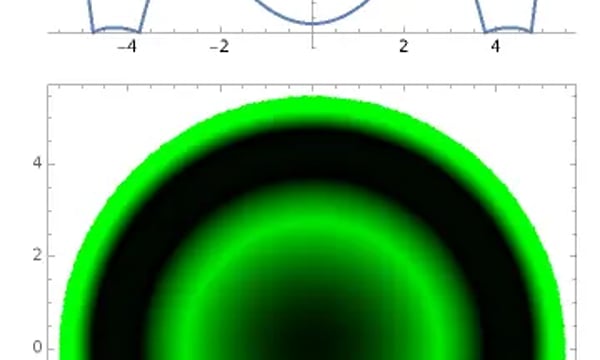
可以用DensityPlot绘制泪液层厚度绕轴旋转的图像,用颜色来表示深度,黑色=0, 绿色越深表示泪液越厚。于是可以得到模拟荧光素染色的图像。
DensityPlot[20*(If[Sqrt[x^2 + y^2] <= PCD/2, Eye[Reye, Qeye, Sqrt[x^2 + y^2]] - OrthoK[Sqrt[x^2 + y^2]], None]),
{x, -PCD/2, PCD/2}, {y, -PCD/2, PCD/2},
ColorFunction -> (Blend[{Black, Green}, #] &), ColorFunctionScaling -> False,PlotPoints -> 100]

可以看出最中心的区域是黑色的,然后逐渐变绿,到达BC与RC交界处的时候是绿色最亮的一环,这里是泪液层最深的地方,然后迅速减淡,在AC弧区域,”适配“良好的话,应该和角膜很接近,于是荧光素的颜色是接近黑色的,出了AC弧进入PC弧以后,为了能够产生泪液交换,于是有一些抬高,荧光素的颜色迅速加深直到边缘。
下一部分,我们可以看看当塑形镜与角膜的曲率半径、Q值不匹配的时候,会发生什么?