为了后续分析方便,我们先重新整理一下代码,有一些简单的Wolfram语言的小技巧,比如用Module标记局部变量之类。写出来并不困难,只是把我们之前已经写好的代码交给GPT4,让AI帮忙整理简化一下即可。
- 首先是计算角膜塑形镜参数的函数:
orthoKParameters[Reye_,Qeye_,Rx_,JF_,BCD_,RCwidth_,ACwidth_,PCD_,PCtear_] := Module[{RCD, ACD, z, BCRfunc, BCR, ACresult, PCresult, RCresult},
RCD=BCD+2*RCwidth;
ACD=RCD+2*ACwidth;
z[R_,Q_,D_, z0_]:=(
c=1/R;
r=D/2;
(c* r^2)/ (1+Sqrt[1-(1+Q)*c^2* r^2]) + z0);
BCRfunc[Reyeinside_,Rxinside_,JFinside_]:=337.5/(337.5/Reyeinside+Rxinside-JFinside);
BCR = BCRfunc[Reye,Rx,JF];
BCz0=-0.003;
RCresult=Solve[
{z[ BCR, 0, BCD, BCz0] == z[RCR,0,BCD,RCz0],
z[ Reye, Qeye, RCD, 0] ==z[RCR,0,RCD,RCz0]},
{RCR,RCz0}];
RCR=RCresult[[1]][[1,2]];
RCz0=RCresult[[1]][[2,2]];
ACresult=NSolve[{
z[ACR,0,RCD,ACz0]==z[Reye, Qeye,RCD,0],
z[ACR,0, ACD, ACz0]==z[Reye, Qeye, ACD, 0]},
{ACR,ACz0}];
ACR=ACresult[[1]][[1,2]];
ACz0=ACresult[[1]][[2,2]];
PCresult=NSolve[{
z[Reye, Qeye, ACD, 0]==z[PCR,0,ACD,PCz0],
z[Reye, Qeye, PCD, 0]==z[PCR,0,PCD,PCz0]+PCtear },
{PCR,PCz0}];
PCR=PCresult[[1]][[1,2]];
PCz0=PCresult[[1]][[2,2]];
{BCR,RCR,ACR,PCR,BCD,RCD,ACD,PCD,BCz0,RCz0,ACz0,PCz0}
]
- 然后根据这些参数,我们可以用一个分段函数来描述角膜塑形镜后表面的矢高
orthoKlens[param_,x_]:= Module[{z},
z[R_,Q_,D_, z0_]:=(
c=1/R;
r=D/2;
(c* r^2)/ (1+Sqrt[1-(1+Q)*c^2* r^2]) + z0);
Piecewise[
{
{z[param[[1]], 0, 2 * x, param[[9]]], 0 <= x < param[[5]] / 2},
{z[param[[2]],0,2*x,param[[10]]], param[[5]] / 2 <= x <param[[6]] / 2},
{z[param[[3]], 0, 2 * x, param[[11]]], param[[6]]/ 2 <= x < param[[7]] / 2},
{z[param[[4]], 0, 2 * x, param[[12]]], param[[7]] / 2 <= x < param[[8]] / 2}
}
]
]
- 类似的,我们还可以定义一个描述眼表角膜矢高的函数。其实就是简单的圆锥曲线函数
Eye[R_,Q_,r_]:=Module[{c},
c=1/R;
(c* r^2)/ (1+Sqrt[1-(1+Q)*c^2* r^2])]
- 通过计算两者的矢高差,我们可以计算出泪液层的厚度,泪液层不会是负的,所以如果泪液层厚度最小值是负值,那么应该把它挪到0, 考虑到我们的设计,最小值只会出现在BC弧起点、AC弧起点和AC弧终点
SagDiff[Rp_,Qp_, param_, x_]:=Eye[Rp,Qp,x]-orthoKlens[param,x]
Tear[Rp_,Qp_, param_, x_]:=SagDiff[Rp,Qp, param, x]-Min[
{SagDiff[Rp,Qp, param, 0],SagDiff[Rp,Qp, param, param[[6]]/2],SagDiff[Rp,Qp, param, param[[7]]/2]}]
- 最后,为了分析方便,还需要做一个绘图函数,可以绘制出泪液层的厚度,并且用绿色来模拟荧光素染色的情况。
DrawTear[Rp_,Qp_,params]:=Module[{PCD, plot1, plot2},
PCD=params[[8]];
plot1 = Plot[Tear[Rp,Qp,params,Abs[x]],{x,-PCD/2,PCD/2}];
plot2 = DensityPlot[20*(If[Sqrt[x^2 + y^2] <= PCD/2, Tear[Rp,Qp,params,Sqrt[x^2 + y^2]], None]),
{x, -PCD/2, PCD/2}, {y, -PCD/2, PCD/2},
ColorFunction -> (Blend[{Black, Green}, #] &), ColorFunctionScaling -> False,PlotPoints -> 100];
GraphicsColumn[{plot1, plot2}]
]
以上准备活动做完,就可以开始分析了。
我们先生成一个角膜塑形镜的参数,对应模型眼的角膜前表面曲率半径=7.5,Q=-0.2,Rx=-3等等
params=orthoKParameters[7.5,-0.2,-3,0.75,5.5,1,1,11,0.1];
- 我们假设来了一个病人,他/她的角膜前表面曲率半径恰好也是7.5, Q值也是-0.2,那么此时是完美适配的。顺便说,我修改了BC起点与角膜之间的距离设定,这里不应该完全接触,会有几个微米的空隙,我留了3微米。
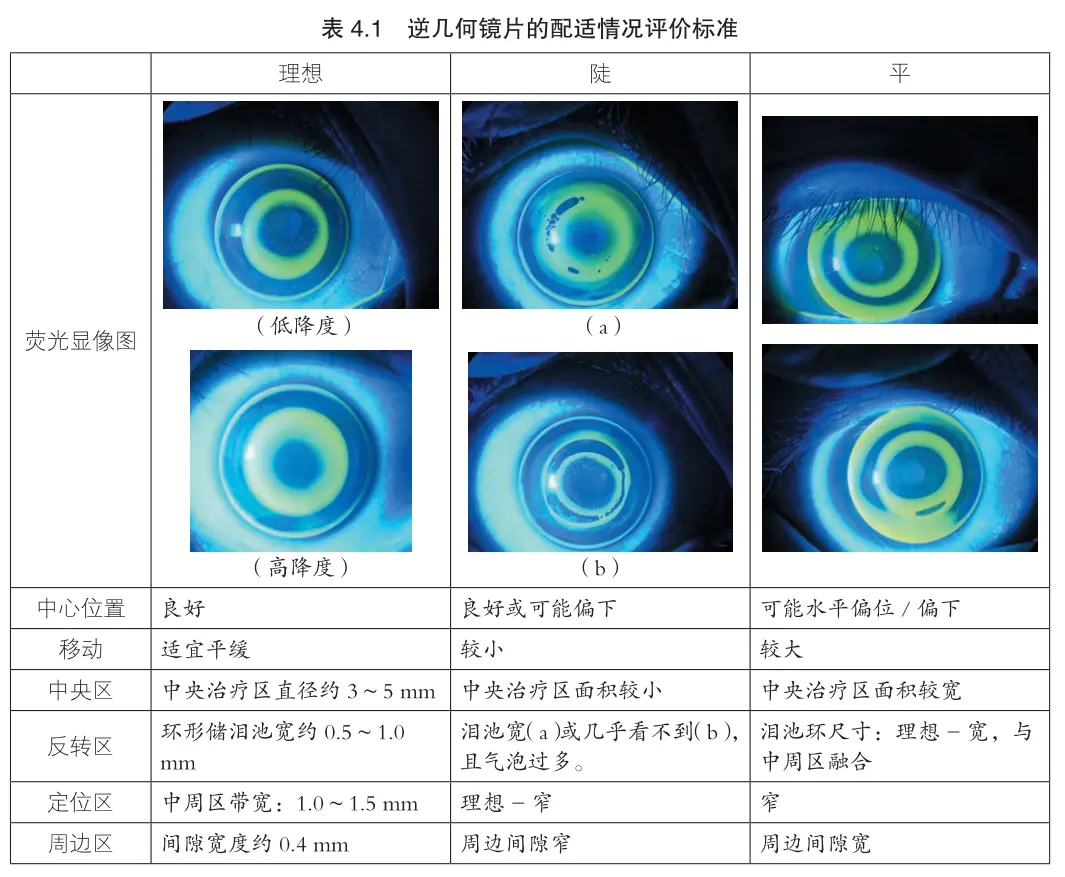
DrawTear[7.5, -0.2, params]

此时,AC弧的起点和终点都与角膜接触,于是这两个位置的泪液层厚度=0。荧光素图上可以看到一个边缘清晰的黑色圆环表示AC弧的范围。
- 第二个病人来了,他/她的角膜前表面曲率半径恰好也是7.5, 但Q值不是-0.2,而是-0.25
DrawTear[7.5, -0.25, params]
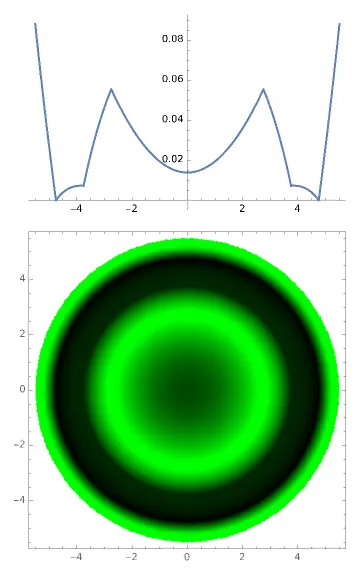
这时候,由于患者的Q值与我们设计所用的模型眼不同,于是不能完全吻合了,AC弧的起点抬高了。荧光素图上可以看出AC环內缘有一些模糊。是的,当你在临床看病人的时候,如果感觉AC弧所对应染色边缘有些模糊,那么说明那里并没有和角膜接触。同时,角膜中心与BC弧之间的距离增加了,根据现有的角膜塑形理论,塑形的作用力是由泪液层不同位置的厚度差决定的,最大作用力是与最大最小泪液层厚度比相关的,现在这个比值减小了,塑形力会减弱。同时由于RC弧也抬高了,塑形力不足时,可能难以将角膜在RC弧区域塑造成一个局部的“凸透镜”,于是形成的周边近视离焦量可能不足,造成对近视进展控制的能力不足。这个孩子可能近视进展的速度比较快。
- 第三个病人进来了,他/她的角膜前表面曲率半径恰好也是7.5, 但Q值不是-0.2,而是-0.10
DrawTear[7.5, -0.10, params]
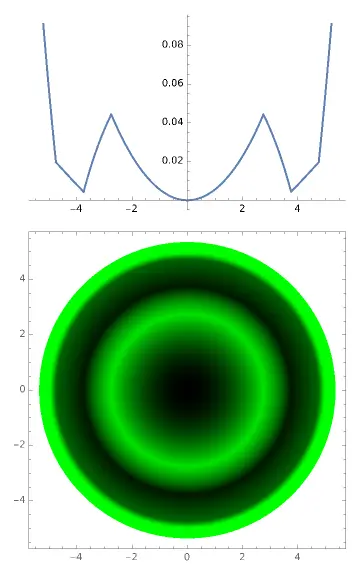
这个情况很糟糕,患者的角膜中心直接与角膜塑形镜中心接触了,AC弧完全不能接触到角膜上,起不到支撑的作用。这时候镜片会像跷跷板一样偏位,直到一侧AC弧的起点接触到角膜,至少形成两点支撑,才会停下来。如果你在验配时把这个病人放走,那么下一次复查的时候,做角膜地形图的时候,你才发现镜片偏位了。如果偏位厉害,你只好让患者停戴,然后再更换镜片。
现在请阅读《角膜塑形术临床实践》第4章,表4.1,看看能否加深你对塑形镜验配的理解