几个月前的一天下午,我去幼儿园接小朋友,却发现三个老师都围着他。我以为发生了什么事情,仔细一看,才发现老师在问他数学题,从一位数加法,到两位数加法,他都能对答如流,最后老师甚至还问了三位数加法,他想了想,也答出来了。
老师们很惊讶,因为德国的幼儿园是“纯玩”,不教任何“正经”东西的,所以即便有些孩子对数字有点概念,也仅限于数数和最简单的加减法而已。遇到一个会三位数加减法的小孩,他们的意外也情有可原。
然后她们问我:你们家孩子怎么这么聪明?这么小就把数学学得这么好了?
“这个……”,我想了想,要认真解释起来,还真得花一番功夫。
正当我犹豫的时候,一位老师给出了答案:“他们是中国来的,中国人的数学就是好呀”,大家都笑了。
“中国人的数学就是好吗?”回家的路上,我一直在思考这个问题,因为我之前从来没想过这回事。而且随着见的东西越来越多,我也越来越深刻感觉,许多东西根本与国籍、人种、肤色无关,而只与学习方法、经验有关,数学也是这样。
因此,所谓“中国人的数学就是好”,大概是广泛流传的刻板印象——我家小朋友学数学,跟“中国人”关系并不大。
下面,我就来现身说法,讲讲他是怎么学数学的。
一
从零开始学数学,一定是从认识数字和数数开始的,在任何国家、任何文化里,都是如此。
而根据现代的心理学研究,人类对于数字的认知,对于简单加减法的了解,基本都没有别的窍门,完全取决于“熟练”程度。换句话说,看到一个数字,认出它是几,这基本靠背。同样,十以内的加减法也是靠背,背到大脑中有一张表,随时可以按图索骥,查表得到结果。
所以,小孩学数学的最早的阶段,就是要在不断重复中熟悉数字,熟悉最基本的加减法。这里的关键是“不断重复”,不过,同样是重复,有些办法可以很机械很折磨人,也有些办法可以很快乐很让人着迷。
在我小时候,父亲说过一句让我印象深刻的话:“玩也要动脑筋。”在听到那句话之前,我总是把“动脑筋”等同于正襟危坐、一丝不苟的学习,与“玩”是天然绝缘的。在听到那句话之后,我就意识到世界上有无数地方都可以动脑筋,也值得动脑筋,当然也包括“玩”。而且,动脑筋并不总是让人苦恼,反而能带来许多乐趣。
所以,自己成为父亲之后,我也秉承着“玩也要动脑筋”的观念,不过做了一点改进:在小朋友玩的时候,我先动脑筋,然后刺激他自己动脑筋。
德国许多公司为了拉动销售,都面对儿童做宣传。以不准点知名的德国铁路(DB)也是如此,每几个月就会到幼儿园派发小册子,里面包括火车的知识、好玩的景点,照例也要提供一些纸上的游戏让孩子玩,其中就包括游戏棋盘。
说是“棋盘”,其实是一段绕来绕去的路,由许多格子组成,每个格子都有编号,小朋友从起点出发,避开陷阱,找到捷径,有时甚至要避开死胡同,最终抵达终点,就算成功。在幼儿园里,有许多小朋友喜欢用食指指着棋盘比赛,甚至着迷上瘾。

这是我们玩过千百遍的棋盘和骰子
发现自己家的小朋友也喜欢玩这个游戏之后,我就动起了脑筋:既然棋盘上每个格子都有编号,而且编号是连续的,不妨拿它们来认识数字。
于是我去超市买了几个骰子,用硬币作为每个人的棋子,跟他做游戏。每扔一次骰子,就根据骰子的点数前进几步。这样玩了一个礼拜,他已经可以一眼认出6以下的数字了。
此时游戏的玩法可以升级,每次投两个骰子,走的步数是两个骰子的点数之和。在移动棋子之前,先算出来要走的步数,如果算错了则要罚停在原地。玩了差不多两个礼拜,算两个骰子的点数之和对他来说已经如同条件反射了。
此时游戏的玩法可以继续升级,把骰子的数量增加到三个。如果能把三个骰子的点数之和都算对,那么20以内的加减法几乎没问题了。
然后可以继续升级玩法,移动棋子时不容许按照点数一路数过去,比如当前所在位置的编号是20,点数是6,不能数“一、二、三、四、五、六”一直走到编号26的位置,而是要内心算好,一下子跳到终点。如果孩子能熟练计算20以内的加减法,那么顺理成章地,超过20的加减法也不会是问题。
我印象里,我们几乎每天吃完晚饭下几盘棋,前后总共花了不到2个月时间,小朋友就熟练掌握了100以内的简单加法,完全没有任何痛苦的感觉。这正应了那句话,“玩也要动脑筋”,我先动脑筋,再刺激他动脑筋。
二
说来惭愧,我要到上了大学,才知道“数学不是科学”。
数学不是科学,或者更准确地说,数学不是自然科学,因为它虽然有公理、有定律、严格依赖逻辑推演,但数学的概念是抽象的,数学本身是无法观测的,更无法用实验来验证和证伪。这也就意味着,对于高度依赖形象思维的儿童来说,学习数学真的不是一回容易的事情。
举例来说,大人或许觉得,“2个苹果+3个苹果=5个苹果”是天经地义的,“2本书+3本书=5本书”也是天经地义的,所以“2+3=5”就是顺理成章的,却忽略了一点:要理解2+3=5,首先必须能把2、3、5这些数字从现实生活的对象中抽象出来,对于幼儿来说,抽象本身就是很大的挑战了。
所以,要让幼儿学好数学,形象化的方法无疑更合适。但是成年人往往习惯了抽象的概念化的表达,认为形象化的办法成本高、效率低。
所幸,我们遇到了幼儿数学节目:Numberblocks。
Numberblocks是英国BBC出品的儿童数学节目,曾经获得过多种奖项。Numberblocks通过符合孩子认知特性的、生动有趣的系列动画,一步步完成孩子的数学启蒙。

它分五个阶段,下面我简单介绍开始的三个阶段:
第一阶段:介绍最简单的1-5五个数字,认识它们,会计数、比较大小、排序,能完成简单的加减法。这个阶段,每个数字都是不同的角色,有自己鲜明的个性。孩子会像记住动画片里的主人公一样,记住这5个数字。

第二阶段:认识的数字可以扩展到10。知道数字可以结对(number bonds),比如1+9=2+8=3+7。能区分奇数和偶数,认识平方数,认识形状。

在这个阶段,同一个数字可以变形为不同的样子,比如8,它一会儿是排成1列的8个小方块,一会儿是2列的4个小方块,一会儿是4列的2个小方块。我见过许多小朋友做题时搞不清楚为什么2*3=3*2,而家长气得七窍生烟,如果孩子看了8的“变形过程”,就一目了然了。另外奇数也很形象,那就是排成两列之后,“头上总还顶着一个格子”(我家小朋友的描述)。

8可以是这样的

6可以是这样的
第三阶段:学习数字的更多变体,比如加倍、折半、乘法、除法、因数分解。我以前认为这些计算对学龄前孩子来说太高阶,跟小朋友一起看了Numberblocks才了解,其实根本不是这样。孩子看过36的多种变形(2*18, 3*12, 4*9, 6*6)之后就自然对因数分解有了认识,甚至能理解素数“就是永远只能排成一列的数”。
在陪孩子看Numberblocks的时候我经常感叹,原来教学视频还能做得这样妙趣横生,又与生活那么紧密相关。举个例子,49这个平方数(Square)上场是个正方形,无论从哪个方向看,都可以完美对应到七色彩虹。由此催生的孩子的认知远远超过了我作为家长的想象,在这之前,我从来没想过,学龄前孩子不但能认识平方数,还认识立方数。
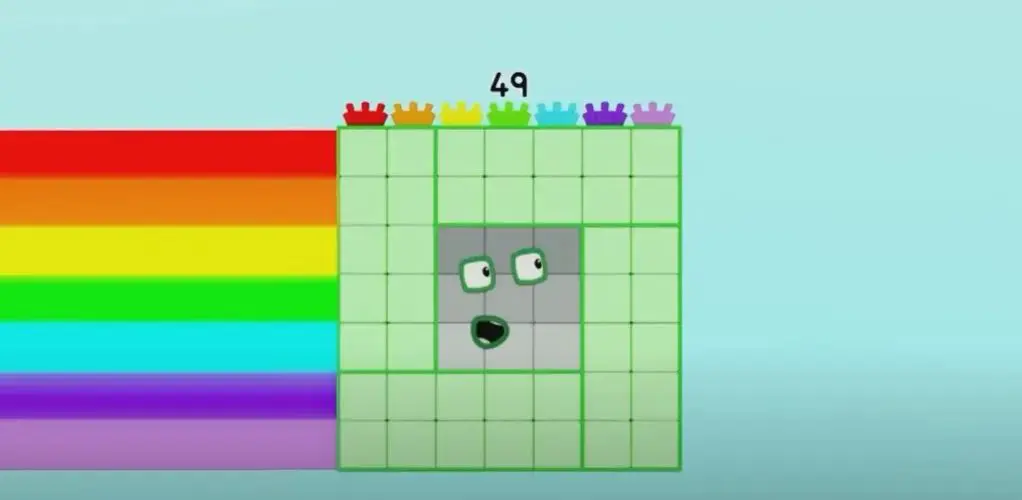
更妙的是,Numberblocks中各个数字的许多发言是儿歌的方式,所以小朋友完全可以跟着唱。不夸张地说,哪怕没有学过英语的孩子,看这部动画也没有任何困难,甚至可以既学数学又学英语。
我知道有许多家长会强调让小孩背诵九九口诀表。无可否认,因为中文独具的每个数一个音节的语言特性,乘法口诀表显得尤其规律、高效,这是中文的独特优势。但九九口诀表不等于数学,它是基于纯数字的抽象。在孩子还没有完全从形象思维进入到概念思维的时候,一味强调九九口诀表,往往可能得不偿失。
相反,类似Numberblocks这样形象的认知方式,尽管不如九九口诀表整齐,给孩子留下的印象可能更深。我家小朋友在远远还没有熟练九九口诀表的时候,就已经对100以内的平方数(Square)、立方数(Cube)如数家珍。我觉得,这不是坏事。
说句题外话,如果你发现自己的孩子很喜欢Numberblocks的动画,那么不妨也去看看Alphablocks,仍然是BBC出品,形式相同,只不过学习的对象是字母和单词。

而且这两部动画还有交集,Numberblocks的数字住在一个星球,Alphablocks的字母住在另一个星球,有一天它们相遇了……

三
我小时候也搞过数学竞赛,还拿过一些奖项。但是等到进大学了发现许多基础的问题我仍然不明白,比如小学就知道的诀窍“能被3(或9)整除的数,各位数字加起来是3(或9)的倍数”,我却不懂为什么,也无法证明。还有圆周率π,它为什么是无理数,而不是有理数?
等我搞明白了这些问题才发现,以前的许多“数学知识”无非是诀窍而已,完全不成体系,是散落的碎片。而如果数学知识不成体系,就只能解答特定类型的题目而已,无法把它们融会贯通,也就没法充分发挥它们的价值。
我见到有不少家长夸耀自己孩子“数学好”。然而,他们拿出来夸耀的往往是孩子做题有多厉害,竞赛拿了什么奖,却很少看到孩子的头脑展现出真正的数学思想,也很少看到孩子对数学本身有什么兴趣。
数学,不能这样学。这样的悲剧,不应该继续重演。
一个偶然的机会,我遇到了美国著名华人数学家伍鸿熙教授的《数学家讲解小学数学》。我确定,要想让孩子学好数学,这就是我想要找的书。

粗看起来,这本书提到的概念都局限于小学数学。但是仔细阅读就会发现,伍教授为每个概念都做了“寻根”,换句话说,他能描绘出每个概念在数学这个学科体系中的位置,与周边概念的关联。
姑且列举让我印象深刻的几个点。伍教授非常强调数轴的作用,“在本书中,关于数的讨论离不开数轴”。我本来没想到数轴这么有用,但仔细看下去才发现他是用心良苦。即便在美国,数学老师也经常用“切比萨”的例子来讲解分数,这就造成孩子无法理解“55英里的2/3”,因为“55英里不可能是一张比萨饼”。如果一开始就强调,分数也是数轴上的一个点,就不会有这种问题。
那么,分数为什么是数轴上的一个点,而不是一条线段呢?在本书中,伍教授也给出了详细的解释。反正我看完是相当服气,也知道以后给小孩讲解分数时,既不要用“比萨饼”也不要用“线段”,正本清源,以绝后患。
那么,教幼儿数学,纠结这些细节有用吗?以我的经验,还真有用。
我家小朋友学加法时,一度总是被“空白”困扰。24+57=81,这对他来说没有问题,因为对位加法,每一位都可以对上,有进位也不难理解。但是124+57就让他困惑不已,因为57没有百位,不知道1怎么和空白相加。
等我看了伍教授书中关于计数法的章节才恍然大悟,原来从一开始就可以告诉孩子,57可以念作“五十七”,也可以念作“零百五十七”,甚至可以念作“零千零百五十七”……换句话说,之前的各位都是0,只是为了书写方便把它们省略了而已。在需要的时候,我们可以随时让它们现形。
故而,124+57其实就是124+057,如此一来,对位加法就顺理成章了。
实际上,这也是我最推荐的《数学家讲解小学数学》的使用方式,就是家长先仔细阅读这本书,搞懂其中的概念,积累自己的知识储备。在与孩子交流的时候,家长“按需输出”就好,既保证概念符合孩子当前的认知水平,又树立正确的观念,为将来更高级的认知埋下伏笔。
回到本文开始的故事。在回家的路上,我问小朋友,“老师怎么发现你会算数的?”
他腼腆一笑说:“老师今天清点人数,两个班,每个班有多少人,大家一起吃饭要准备多少碟子,我平时玩骰子游戏习惯了,听到就帮她算出来,她就发现了。”
所以至少在我家,数学学得好和是哪国人,其实没有必然关系。



