本部分的gemini动态视图演示： https://gemini.google.com/share/8d119703fa8a

第三部分：视觉质量评估

第 8 章：视觉质量的“元凶”：PSF 与卷积

致 Dr. X：

上一章结束时，我们用 Zernike 多项式这套“乐高积木”，成功搭建出了患者角膜波前像差的模型。

你看着那个 $Z_4^0$ 系数（球差），脑海中浮现出了一个 “中心平坦、边缘陡峭的墨西哥草帽” 。这非常棒。但这仅仅完成了一半的工作。因为你的患者并没有坐在诊室里抱怨：“医生，我的波前变成了草帽状。”

他们只会说：“医生，我看东西有鬼影。”

这就是本章的任务。我们需要跨越从“物理形状”到“视觉症状”的最后一道鸿沟。如果说第 7 章的波前是“因”，那么本章我们要寻找的就是“果”。

我们要介绍两个听起来很数学，但实际上极其直观的概念：点扩散函数 (PSF) 和 卷积 (Convolution)。

请放心，我们不需要微积分。这一次，我们把你的浏览器变成 Photoshop。

1. PSF：你眼睛里的“画笔”

Dr. X，让我们换个角度思考成像过程。想象你的眼睛不是在“接收”图像，而是一位不知疲倦的画家，正在把外部世界的景象“画”在视网膜上。

这位画家作画的工具，不是像素打印机，而是一支 “画笔”。

这就引出了 点扩散函数 (PSF, Point Spread Function) 的真谛：

PSF，就是你眼睛这支“画笔”的笔尖形状。

完美视力（衍射极限）：笔尖极细，就像一支精密的针管笔（受限于我们在第 4 章讲过的艾里斑）。用它画出来的世界，细节锐利，边缘清晰。
球差（光晕）：笔尖“炸毛”了。针尖周围粘了一圈散开的刷毛。用这种笔作画，所有物体的周围都会自带一圈雾气。
彗差（拖尾）：笔尖被压歪了，分叉了，像个破损的扫把。用它画画，每一笔都会向同一个方向拖出一个长长的尾巴。

当我们计算 PSF 时，我们其实是在问计算机：“给定第 7 章那个扭曲的波前，光线穿过它后，会在视网膜上砸出一个什么样的光斑？”

2. 实验 8.1：Zernike-PSF 因果联动台

说的再多，不如亲眼看一看。

既然我们知道透镜是一台天然的傅里叶计算机（第 6 章），我们就可以直接算出这支“画笔”现在的样子。

Dr. X，这是本书目前为止最强大的工具之一。在下方的实验中，我们将同时展示 “因”（波前形状） 和 “果”（视网膜上的光斑）。

请点击下方的链接，或直接运行这段代码。请特别注意代码中的注释，我已将它们从“代码语言”翻译成了“眼科语言”。

(* 启动 Zernike-PSF 联动模拟器 *)
Manipulate[
Module[{totalWavefront, phase, pupilFunction, fft, psf, n = 128},
 
 (* --- 1. 制造波前 (The Cause) --- *)
 (* 使用 Zernike 积木搭建波前形状 *)
 (* r 和 theta 是瞳孔平面上的极坐标 *)
 totalWavefront = Table[
   Module[{r, theta},
    (* 将网格坐标转换为极坐标，模拟圆形瞳孔 *)
    r = Sqrt[x^2 + y^2];
    theta = ArcTan[x, y];
    
    (* 定义瞳孔孔径：超出半径1的区域没有光线通过 *)
    If[r > 1, 0,
     (* 叠加 Zernike 积木 *)
     (* Z(2,0) 离焦: 碗状 *)
     cDef * (Sqrt[3] * (2 r^2 - 1)) + 
     (* Z(2,2) 散光: 马鞍状 *)
     cAstig * (Sqrt[6] * r^2 * Cos[2 theta]) + 
     (* Z(3,1) 彗差: 滑梯状 *)
     cComa * (Sqrt[8] * (3 r^3 - 2 r) * Cos[theta]) + 
     (* Z(4,0) 球差: 墨西哥草帽状 *)
     cSph * (Sqrt[5] * (6 r^4 - 6 r^2 + 1))
    ]
   ], {y, -1.2, 1.2, 2.4/(n - 1)}, {x, -1.2, 1.2, 2.4/(n - 1)}
  ];

 (* --- 2. 模拟成像过程 (The Physics) --- *)
 
 (* 计算光波在瞳孔处的相位变化 *)
 (* 像差越大，相位扭曲越严重 *)
 phase = Exp[I * 2 * Pi * totalWavefront];
 
 (* 让光线穿过晶状体并传播到视网膜 *)
 (* Fourier 变换模拟了透镜的聚焦作用 *)
 fft = Fourier[phase];
 
 (* --- 3. 计算视网膜像 (The Effect) --- *)
 
 (* 计算感光细胞接收到的光强 (PSF) *)
 (* RotateRight 用于将光轴中心对准视网膜黄斑中心 *)
 psf = Abs[RotateRight[fft, {n/2, n/2}]]^2;
 
 (* --- 4. 视觉呈现 --- *)
 Grid[{
   {Style["原因：波前像差 (Wavefront)", Bold, Blue, 14], 
    Style["结果：点扩散函数 (PSF)", Bold, Red, 14]},
   {
    (* 左图：展示波前的 3D 地形 *)
    ListPlot3D[totalWavefront, 
     PlotRange -> {-1, 1}, 
     ColorFunction -> "Rainbow", 
     Boxed -> False, Axes -> False, Mesh -> None, 
     ImageSize -> 300, ViewPoint -> {1.5, -2.4, 1.5}],
    
    (* 右图：展示视网膜上的光斑形状 *)
    (* 使用 ImageAdjust 模拟人眼对微弱光晕的适应能力 *)
    Image[ImageAdjust[Image[psf], {0, 0, 0.5}], ImageSize -> 300, Magnification -> 2]
   }
  }]
 ],

(* --- 控制面板：你的光学处方台 --- *)
Style["低阶像差 (基础屈光)", Bold, 12],
{{cDef, 0, "离焦 Z(2,0) [近视/远视]"}, -0.5, 0.5, 0.05, Appearance -> "Labeled"},
{{cAstig, 0, "散光 Z(2,2) [规则散光]"}, -0.5, 0.5, 0.05, Appearance -> "Labeled"},
Delimiter,
Style["高阶像差 (夜间视力杀手)", Bold, 12, Red],
{{cComa, 0, "彗差 Z(3,1) [拖尾/星芒]"}, -0.5, 0.5, 0.05, Appearance -> "Labeled"},
{{cSph, 0, "球差 Z(4,0) [光晕/Halo]"}, -0.5, 0.5, 0.05, Appearance -> "Labeled"}
]

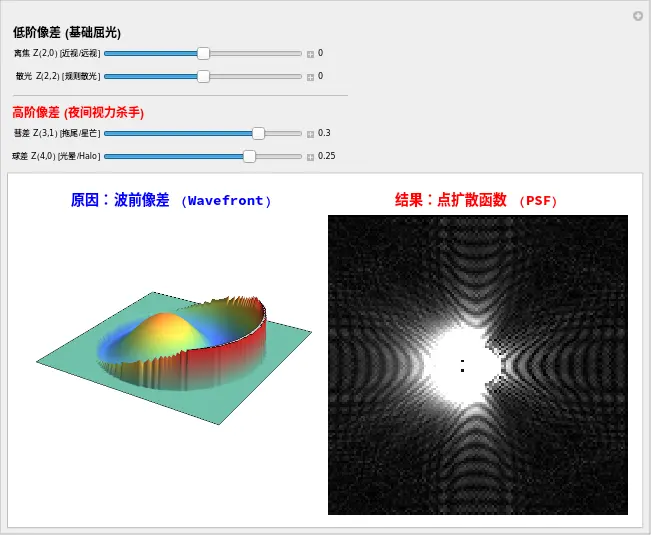
An image to describe post

见证“因果”时刻

Dr. X，现在你就是首席光学工程师。请分别拖动这些滑块，观察右侧那个白点（PSF）的变化，这就是你的患者看到的真实世界。

制造“光晕” (Spherical = 0.4)：
- 拖动球差 Z(4,0) 滑块。
- 看左边：波前变成了经典的“墨西哥草帽”。
- 看右边：注意那个光点！中心虽然还亮，但周围出现了一圈弥散的光环。
- 临床联系：这就是你那位 LASIK 术后患者在晚上看到的车灯。那个光环就是 “光晕 (Halo)” 。
制造“扫把星” (Coma = 0.4)：
- 将球差归零，拖动彗差 Z(3,1) 滑块。
- 看左边：波前像滑梯一样歪了。
- 看右边：光点不再是圆的，它拖出了一条长长的尾巴，像个彗星。
- 临床联系：这就是圆锥角膜或人工晶体偏位（IOL Tilt）患者看到的 “星芒”或“单眼复视” 。
制造“散光” (Astigmatism = 0.4)：
- 看右边：光点被拉长成了一个椭圆。这就是为什么散光患者看月亮会有重影。

3. 卷积：从“一个点”到“整个世界”

你可能会问：“好的，我明白‘一个点’变成了‘光晕’。但病人看的是视力表，是字母 E，不是星星。那会变成什么样？”

这就要用到第二个核心概念：卷积 (Convolution)。

卷积听起来很深奥，但它的本质就是 “描边”。

想象一下，你要画一个字母“E”：

在视网膜上，这个“E”是由成千上万个微小的“光点”组成的。
如果眼睛有像差，每一个“光点”都会变成你刚才看到的那个 “带光晕的脏点” (PSF)。
卷积就是：拿着这支变形的画笔（PSF），沿着视力表上“E”的轮廓，重新描一遍。

如果画笔很大（离焦），笔画就会粗到粘在一起 $\rightarrow$ 模糊。
如果画笔分叉（彗差），每一笔都会向下拖尾 $\rightarrow$ 重影。

4. 实验 8.2：亲手“卷积”视力表

别光听我说。让我们用你刚才制造的那支“脏画笔”，去画一个视力表。

下方的代码会加载一个标准的“E”字，然后让你用不同的像差去“污染”它。

(* 启动视力表卷积实验 *)
Manipulate[
Module[{totalWavefront, phase, pupilFunction, psf, imgE, convolvedImage, n = 128},
 
 (* --- 1. 准备“画布”：生成视标 E --- *)
 imgE = Rasterize[Style["E", FontFamily -> "Arial", FontSize -> 80, Bold, FontColor -> White, Background -> Black], RasterSize -> n, ImageSize -> n];
 imgE = ImageAdjust[ColorConvert[imgE, "Grayscale"]];

 (* --- 2. 准备“画笔”：计算 PSF --- *)
 (* (这部分物理计算与实验 8.1 相同，但在后台运行) *)
 totalWavefront = Table[
   Module[{r, theta},
    r = Sqrt[x^2 + y^2]; theta = ArcTan[x, y];
    If[r > 1, 0,
     cDef * (Sqrt[3] * (2 r^2 - 1)) + 
     cComa * (Sqrt[8] * (3 r^3 - 2 r) * Cos[theta]) + 
     cSph * (Sqrt[5] * (6 r^4 - 6 r^2 + 1))
    ]
   ], {y, -1.2, 1.2, 2.4/(n - 1)}, {x, -1.2, 1.2, 2.4/(n - 1)}
  ];
 
 phase = Exp[I * 2 * Pi * totalWavefront];
 
 (* 计算画笔形状 (PSF) *)
 psf = Abs[RotateRight[Fourier[phase], {n/2, n/2}]]^2;
 (* 归一化画笔，保证墨水量守恒 *)
 psf = psf / Total[Flatten[psf]]; 

 (* --- 3. 执行“描边”：卷积 (Convolution) --- *)
 (* 使用 ImageConvolve 函数，用 PSF 画笔重绘 E 字 *)
 convolvedImage = ImageConvolve[imgE, Image[psf]];

 (* --- 4. 结果展示 --- *)
 Grid[{
   {Style["1. 你的画笔 (PSF)", Bold, Blue], 
    Style["2. 原始视标", Bold, Green], 
    Style["3. 病人看到的 (卷积后)", Bold, Red]},
   {
    (* 显示对数增强的 PSF，以便看清光晕细节 *)
    Image[ImageAdjust[Image[Log[psf + 10^-7]]], ImageSize -> 150, Magnification -> 2],
    Image[imgE, ImageSize -> 150],
    (* 显示最终模糊的 E *)
    Image[ImageAdjust[convolvedImage], ImageSize -> 150]
   }
  }, Spacings -> {2, 2}, Alignment -> Center]
 ],

(* --- 控制面板 --- *)
Style["像差控制", Bold, 12],
{{cDef, 0.0, "离焦 (近视/远视)"}, 0, 0.8, 0.05, Appearance -> "Labeled"},
{{cComa, 0, "彗差 (不规则散光)"}, 0, 0.8, 0.05, Appearance -> "Labeled"},
{{cSph, 0, "球差 (夜间眩光)"}, 0, 0.8, 0.05, Appearance -> "Labeled"}
]

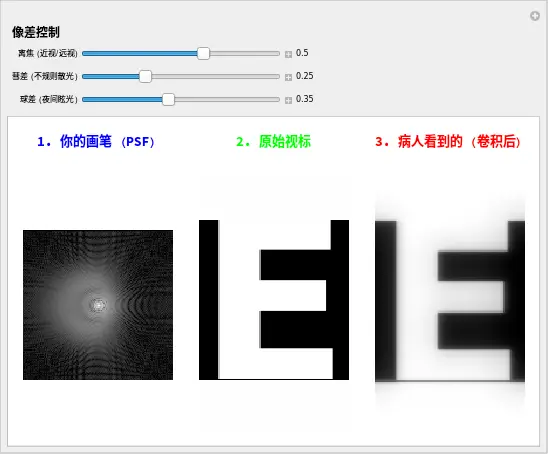
An image to describe post

实验观察指南：

模拟“彗星 E”（彗差）：
- 把离焦归零，增加彗差。
- 观察 PSF：变成了一个小水滴。
- 观察 E 字：天啊！整个字母像是油漆没干就垂直流下来了一样！这种 “垂直拖尾” 是普通眼镜无法矫正的。这正是圆锥角膜病人的典型主诉。
模拟“雾中 E”（球差）：
- 增加球差。
- 观察 PSF：中心亮，周围有一圈雾。
- 观察 E 字：字母的主体居然还是清楚的（甚至能认出来），但在字母周围多了一层白茫茫的雾（对比度下降）。
- 临床洞见：这就是为什么球差病人视力表能看清 1.0，但还是觉得“看不清”！因为球差保留了锐利的中心（高频），但扼杀了对比度（低频）。

5. 为什么视力表在“骗”你？

Dr. X，做完这个实验，你可能已经意识到了一个令人不安的事实。

我们每天用的 Snellen 视力表（那个高对比度的黑白 E），其实是一个非常粗糙的工具。

就像你在实验中看到的：球差 (Spherical Aberration) 严重的病人，因为 PSF 中心依然有一个尖峰，他可能依然能读出那个 E（视力 1.0）。但他看到的 E，是像泡在牛奶里一样，对比度极低。

他对你说：“医生，我能看见它是 E，但我感觉像是在大雾天里看东西。”
如果你只查视力表，你会说：“你视力 1.0，你没事，是心理作用。”
但如果你看懂了 PSF，你就知道：“不，你是对的。你的画笔脏了，你的对比度丢了。”

那么，我们该如何科学地测量这种“丢失的对比度”呢？

既然视力表不行，我们需要一把更精密的尺子。

答案藏在下一章。我们需要 MTF (调制传递函数)。

本章小结：

PSF（点扩散函数）：是眼睛这支“画笔”的笔尖形状。Zernike 像差决定了笔尖有多脏、多歪。
卷积（Convolution）：成像就是用 PSF 这支笔，把外面的世界重新“描”一遍。
从形状到症状：
- 墨西哥草帽波前 $\rightarrow$ 光晕画笔 $\rightarrow$ 雾蒙蒙的视力（球差）。
- 滑梯波前 $\rightarrow$ 拖尾画笔 $\rightarrow$ 重影的视力（彗差）。
视力表的局限：它只能测出 PSF 的“尖峰”在哪，测不出 PSF 周围的“光晕”有多大。

下章预告：

第 9 章：“看清”对比度：MTF、CSF 与 PTF —— 为什么视力 1.5 的人可能不敢开车？

第 9 章：“看清”对比度：MTF、CSF 与 PTF —— 为什么视力 1.5 的人不敢开车？

致 Dr. X：

还记得上一章那个“惨不忍睹”的 E 字吗？

现在，请您暂时忘掉那个 E 字，哪怕只有一分钟。因为本周您遇到了一位让您左右为难的病人——那位白内障术后的老飞行员。

手术极其完美，晶体正位，角膜清亮。

查视力（Snellen）： $1.5 \ (20/13)$ 。简直是鹰眼。

病人主诉：“医生，你在骗我。我看世界就像隔着一层脏玻璃。尤其是阴天，跑道看起来是灰的，不是黑的。我根本不敢降落。”

您指着视力表最后一行：“你看，你连这一行都能看见！”

他摇摇头：“我是看见了，但它们是灰色的，它们没有‘劲’。”

Dr. X，视力表在撒谎。或者更准确地说，它只告诉了您一半的真相。

视力表测量的是 “能不能看见” (Resolution/Acuity)。
病人抱怨的是 “看着舒不舒服” (Contrast/Quality)。

要在科学上描述这种“舒服程度”，我们需要一把比视力表更精密的尺子。这把尺子，就是我们把上一章的 PSF（光斑）再次扔进傅里叶变换机器后，提炼出的眼科光学“圣杯”：MTF (调制传递函数)。

系好安全带。这是本书“二维平面光学”部分的最后一战。我们要揭开“视力 1.5 却看不清”的物理真相。

1. MTF：你的眼睛是一套“音响系统”

还记得第 5 章那个“傅里叶分解器”吗？让我们再次请出那个最完美的比喻：光即声音。

如果把您眼前的景色看作一首交响乐：

低频 (Low Spatial Frequency)：图像的大轮廓（比如视力表上巨大的 0.1 的 E）。这相当于声音里的低音贝斯 (Bass)。
高频 (High Spatial Frequency)：图像的锐利边缘、微小的细节。这相当于声音里的高音小提琴 (Treble)。

您的眼睛，本质上就是一套 “音响播放系统” 。

外界的景象（完美的物体）是“原声母带”。
视网膜上最终的图像，是“音箱播放出来的声音”。

什么是 MTF (Modulation Transfer Function)？

MTF 就是这套音响系统的“保真度曲线” 或者 “各频段的音量旋钮”。它回答了一个问题：当输入 100% 对比度的信号时，这套系统能输出多少？

完美的光学系统 ( $MTF \approx 1$ )：这是一套昂贵的 Hi-Fi 音响。低音雄浑，高音清脆。不管频率多高，对比度几乎不丢失。
有像差的眼睛 ( $MTF$ 下降)：这是一个泡了水的蓝牙音箱。低音（大轮廓）可能还听得见，但高音（细节）变得嘶哑、浑浊。原本锐利的黑白边缘，变成了灰蒙蒙的一团。

所以，当那位老飞行员说“看得见 E，但是灰蒙蒙”时，用物理语言翻译就是：

“我的低频 MTF 还可以（所以能认出轮廓），但我的中高频 MTF 掉得太厉害了（对比度丢失）！”

2. 全链路物理：从 Zernike 到 MTF

那么，这根神奇的 MTF 曲线是怎么算出来的？它不需要额外的魔法，它就藏在我们上一章讲的 PSF 里。

这是一个非常优美（也很残酷）的数学链条，它是所有像差仪的核心算法逻辑。请务必在脑海中建立这个流程：

Zernike 系数 (输入)：像差的“乐高积木”清单。
- $\downarrow$ (线性叠加)
波前像差 (Wavefront)：角膜/晶体在物理上的扭曲形状。
- $\downarrow$ (傅里叶变换 + 取模平方)
PSF (点扩散函数)：视网膜上的一个光斑形状（那支“画笔”）。
- $\downarrow$ (再次傅里叶变换!)
OTF (光学传递函数)：这是最终的终点，它包含两部分：
- 幅度 (Magnitude) $\rightarrow$ MTF：对比度传了多少？（变淡了吗？）
- 相位 (Phase) $\rightarrow$ PTF：位置移了多少？（变歪了吗？）

一句话总结：MTF 就是 PSF 的傅里叶变换的幅度。

如果 PSF 是一个极细的针尖（完美），它的频谱（MTF）就是一条平直的高线（所有频率完美通过）。
如果 PSF 变成了一团云雾（球差），它的频谱（MTF）就会在高频区迅速塌陷。

3. 实验 9.1：全链路仿真实验室

Dr. X，别只听我说。我们要构建本书目前为止最复杂的“全链路”模型。

这一次，我们将同时看到这条链上的每一个环节。

你的任务：破坏这只完美的眼睛，然后看看 MTF 曲线和视力表是如何崩塌的。

请点击下方的 Wolfram Cloud 链接，或直接运行代码。

[特别提示] 为了让您读懂代码，我已将原本枯燥的计算机函数，全部翻译成了“医学术语”。请注意阅读注释！

(* 启动全链路光学模拟器 *)
Manipulate[
 Module[{totalWavefront, pupilFunction, fftPupil, psf, otf, mtfFull, mtfCurve, ptfFull,
   simulatedE, simulatedSin, psfDataLog, psfDisplay, wavefrontDisplay, n = 128},


  (* --- 1. 光学核心计算 (The Physics Engine) --- *)


  (* A. 组合波前: 用 Zernike 积木搭建角膜形状 *)
  totalWavefront = Table[
    Module[{r, theta},
     r = Sqrt[x^2 + y^2]; theta = ArcTan[x, y];
     If[r > 1, 0, (* 瞳孔限制 *)
      (cDef * Sqrt[3] * (2 r^2 - 1)) +           (* 离焦 *)
      (cAstig * Sqrt[6] * r^2 * Cos[2 theta]) +  (* 散光 *)
      (cComa * Sqrt[8] * (3 r^3 - 2 r) * Cos[theta]) + (* 彗差 *)
      (cSph * Sqrt[5] * (6 r^4 - 6 r^2 + 1))     (* 球差 *)
      ]
    ], {y, -1, 1, 2./(n - 1)}, {x, -1, 1, 2./(n - 1)}];


  (* B. 瞳孔函数: 将波前高度转化为光波相位 *)
  pupilFunction = Exp[I * 4 * Pi * totalWavefront];


  (* C. 计算 PSF: 模拟光线穿过透镜聚焦在视网膜上 *)
  fftPupil = Fourier[pupilFunction]; (* Fourier = 透镜聚焦 *)
  psf = Abs[RotateRight[fftPupil, {n/2, n/2}]]^2; (* Abs^2 = 视网膜感光 *)
  psf = psf / Total[Flatten[psf]]; (* 能量守恒归一化 *)


  (* D. 计算 MTF/PTF: 对 PSF 进行频谱分析 *)
  otf = Fourier[psf]; (* 再次 Fourier = 分析画笔的频率响应 *)
  otf = RotateRight[otf, {n/2, n/2}];
  
  (* MTF: 取模 (Magnitude) -> 对比度保留了多少 *)
  mtfFull = Abs[otf];
  mtfFull = mtfFull / Max[mtfFull]; (* 归一化 *)
  mtfCurve = mtfFull[[n/2, n/2 ;; n - 5]]; (* 提取一维曲线用于绘图 *)
  
  (* PTF: 取辐角 (Argument) -> 相位移动了多少 *)
  ptfFull = Arg[otf];


  (* --- 2. 视觉仿真 (卷积 Convolution) --- *)
  (* 用计算出的 PSF 画笔，重新描绘视力表 E 和正弦条纹 *)
  simulatedE = ImageConvolve[imgE, Image[psf]]; 
  simulatedSin = ImageConvolve[imgSin, Image[psf]];


  (* --- 3. 仪表盘可视化布局 --- *)
  Grid[{
    {Style["1. 波前像差 (Topography)", Bold, Blue], 
     Style["2. 点扩散函数 (Log PSF)", Bold, Purple], 
     Style["3. MTF 曲线 (对比度)", Bold, Darker[Green]]},
    
    {
     (* 1. 波前图 *)
     ArrayPlot[totalWavefront, ColorFunction -> "Rainbow", Frame -> False, ImageSize -> 200],
     
     (* 2. PSF 图 (对数增强，模拟人眼适应) *)
     Image[Colorize[Image[Rescale[Log[psf + 10^-9]]], ColorFunction -> "SunsetColors"], ImageSize -> 200],
     
     (* 3. MTF 曲线 *)
     ListLinePlot[mtfCurve, PlotRange -> {0, 1.1}, GridLines -> Automatic, Filling -> Axis, 
      PlotStyle -> {Thick, Darker[Green]}, AxesLabel -> {"Freq", "Contrast"}, ImageSize -> 200]
    },


    {Style["4. 视力表 (Resolution)", Bold], 
     Style["5. CSF 条纹 (Contrast)", Bold], 
     Style["6. 相位传递 (PTF)", Bold]},


    {
     (* 4. 模糊的 E *)
     Image[simulatedE, ImageSize -> 200],
     
     (* 5. 模糊的条纹 *)
     Image[simulatedSin, ImageSize -> 200],
     
     (* 6. PTF 相位图 *)
     Column[{
       If[Abs[cComa] > 0.1, Style["⚠️ 严重相位扭曲", Red, Bold], Style["相位平稳", Green]],
       Image[ImageAdjust[Image[Rescale[ptfFull]]], ImageSize -> 100]
     }, Alignment -> Center]
    }
   }, Spacings -> {1, 1}, Frame -> All, Background -> LightGray]
  ],


 (* --- 控制面板 --- *)
 Style["像差控制器 (单位: 微米)", 14, Bold],
 {{cDef, 0.0, "离焦 Z(2,0) [近视]"}, -0.5, 0.5, 0.05, Appearance -> "Labeled"},
 {{cAstig, 0.0, "散光 Z(2,2) [散光]"}, -0.5, 0.5, 0.05, Appearance -> "Labeled"},
 Delimiter,
 Style["高阶像差 (夜间视力杀手)", 12, Bold, Red],
 {{cComa, 0.0, "彗差 Z(3,1) [拖尾]"}, -0.5, 0.5, 0.05, Appearance -> "Labeled"},
 {{cSph, 0.0, "球差 Z(4,0) [光晕]"}, 0.0, 0.5, 0.05, Appearance -> "Labeled"},
 
 Initialization :> (
  (* 预加载高清素材 *)
  imgE = ImageAdjust[ColorConvert[Rasterize[Style["E", FontFamily -> "Arial", FontSize -> 80, Bold, FontColor -> White, Background -> Black], RasterSize -> 128, ImageSize -> 128], "Grayscale"]];
  imgSin = Image[Table[0.5 + 0.5 * Sin[6 * 2 * Pi * x/2.0], {y, -1., 1., 2./127}, {x, -1., 1., 2./127}]];
 )
]

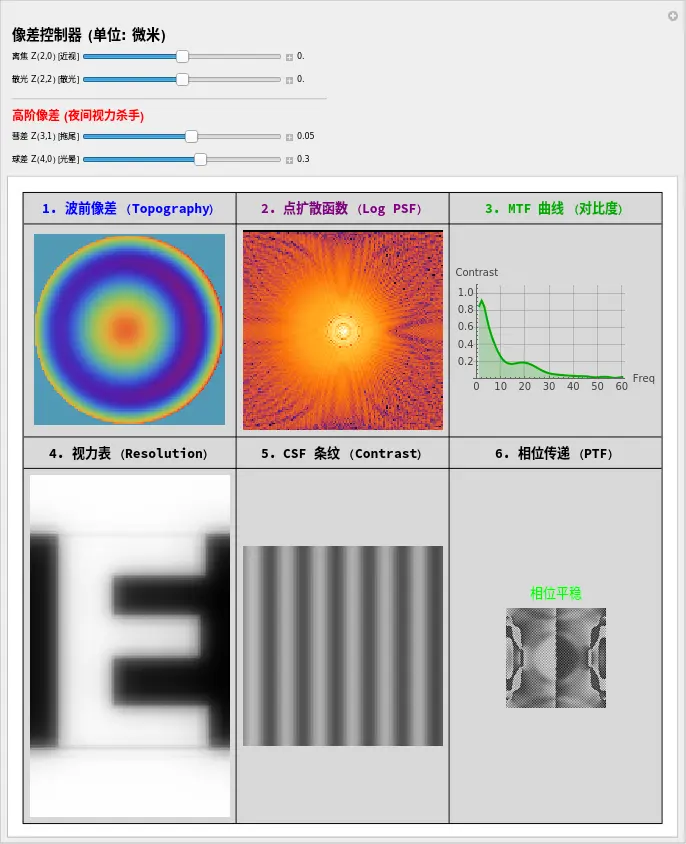
An image to describe post

4. 见证“对比度杀手”：如何解读实验结果

Dr. X，现在您手里拿着这把“光学的解剖刀”。请按以下步骤操作，您会立刻明白那位老飞行员的痛苦。

场景 A：球差的骗局 (The Spherical Deception)

操作：慢慢拉高 Spherical (球差) 滑块到 0.4。
观察 PSF：变成了一个“草帽”，中心有个亮核，周围有一圈大光晕。
观察 MTF 曲线：这是关键！曲线并没有直接掉到 0。它在中低频段（中间部分）塌陷了，但在高频段（最右边）依然顽强地保持在 0 以上。
观察“E”：那个 E 看起来像泡在牛奶里（发灰），但它的边缘依然能分辨！
结论：
- 因为还有高频 (High Freq)，所以视力表还能查出 1.0 甚至 1.2。
- 因为中低频塌陷 (MTF Area)，所以对比度丢了。
- 这就是为什么老飞行员说“看得见，但看不清”。视力表被球差“骗”了。

场景 B：彗差与 PTF 的“鬼影” (The Ghost of PTF)

操作：归零球差，拉高 Coma (彗差) 到 0.4。
观察 PSF：像个扫把星。
观察 E 和条纹：注意！E 字不仅仅是糊了，它发生了位移，甚至向下拖出了一个重影。正弦条纹看起来像是在“蠕动”或变形。
观察 PTF 面板：只有在彗差（不对称像差）出现时，PTF 图才会有剧烈的黑白跳变。
结论：
- MTF 告诉我们图像“淡”了多少。
- PTF (相位传递函数) 告诉我们图像“歪”了多少。
- 大脑非常讨厌 PTF 错误。这就是为什么一点点彗差（如圆锥角膜）就会让人产生单眼复视，极其头晕。

5. 为什么科学家非要用“正弦波” (Sine Wave)？

做完实验，您可能会问：“作者，为什么对比敏感度测试 (CSF) 非要用那些看着让人眼晕的黑白条纹（正弦光栅）？用变淡的 E 字不行吗？”

这是一个极好的问题。答案涉及到一个深刻的数学原理：本征函数 (Eigenfunction)。

Dr. X，请回看您的实验结果：

当您用像差去“污染” E 时，E 的形状变了。它的角变圆了，它长出了尾巴，它甚至变成了两个 E。输入是 E，输出变成了“怪物”。
当您用像差去“污染”正弦条纹时，请仔细看——它依然是正弦条纹！
- 它的间距没变（频率不变）。
- 它的形状没变（还是正弦波）。
- 唯一改变的，只有振幅（变淡了）和相位（平移了）。

在线性光学系统中，正弦波是“天选之子”（本征函数）。

无论您的眼睛有多烂，正弦波进去，出来的永远是正弦波。

所以，科学家只信任正弦波。只有用它，我们才能精确地测出那个“变淡了多少” (MTF)，而不受物体形状畸变（如 E 变成怪物）的干扰。这就是临床上 CSF (对比敏感度函数) 检查的原理。

6. 本章小结：你现在的段位

Dr. X，恭喜您。这一章之后，您看病人的眼光应该已经彻底变了。

以前：您看视力表。1.0 就是好，0.5 就是坏。
现在：您看 MTF。您知道 1.0 的视力可能伴随着惨不忍睹的对比度（球差）。
以前：您觉得眩光是病人“太敏感”。
现在：您知道那是 PSF 的旁瓣在视网膜上肆虐。
以前：您不知道为什么有些像差（彗差）让人头晕。
现在：您知道那是 PTF 在扭曲世界的几何位置。

我们已经彻底征服了“二维平面”的光学（X 轴和 Y 轴）。所有的波前、PSF、MTF，都是在视网膜这个平面上发生的故事。

但是，眼科医生的世界是三维的。我们不仅要看清视网膜表面，我们还要看穿它，看到它的深处。

下章预告：

我们要把傅里叶变换用到极致。我们要把光变成一把手术刀，去切开视网膜的断层。

是的，我们要讲 OCT (光学相干断层扫描)。而您会惊讶地发现，那里面居然也藏着傅里叶的影子，而且是让您意想不到的用法。

[下一步行动]

再次打开上面的 Wolfram Cloud 代码。这次试着把 cDefocus (近视) 和 cSpherical (球差) 混合在一起。你会发现一个惊人的现象：适量的球差居然能缓解近视带来的模糊！（这正是“景深延长型 (EDOF)”人工晶体的秘密，我们以后会讲）。现在，去试试吧！

《眼科傅里叶光学》第三部分：视觉质量评估

第三部分：视觉质量评估

第 8 章：视觉质量的“元凶”：PSF 与卷积

1. PSF：你眼睛里的“画笔”

2. 实验 8.1：Zernike-PSF 因果联动台

3. 卷积：从“一个点”到“整个世界”

4. 实验 8.2：亲手“卷积”视力表

5. 为什么视力表在“骗”你？

本章小结：

下章预告：

第 9 章：“看清”对比度：MTF、CSF 与 PTF —— 为什么视力 1.5 的人不敢开车？

1. MTF：你的眼睛是一套“音响系统”

2. 全链路物理：从 Zernike 到 MTF

3. 实验 9.1：全链路仿真实验室

4. 见证“对比度杀手”：如何解读实验结果

5. 为什么科学家非要用“正弦波” (Sine Wave)？

6. 本章小结：你现在的段位

下章预告：