本章的Gemini动态视图演示: https://gemini.google.com/share/6dc64fff2ec5
第四部分:诊断与治疗的光学
第 10 章:干涉的“奇迹”——OCT 是如何“看穿”视网膜的
致 Dr. X:
如果在你的诊室里随便抓一位视光师,问他:“OCT 的原理是什么?”
他多半会自信地回答:“哦,那就是光做的 B 超。超声波测声音的回声,OCT 测光的回声。”
作为一名已经读到第 10 章的准光学专家,你需要制止这种危险的过度简化。
是的,两者生成的图像看起来很像(都是断层切面),但物理原理有着天壤之别。
超声波的工作原理确实是 “回声定位” (Time of Flight):喊一声,掐表,记录声音弹回来的时间 。因为声速很慢(在水中约 1500 m/s),电子表完全来得及反应。
但光速是 $3 \times 10^8$ 米/秒。光在视网膜神经上皮层里跑个来回,只需要 0.0000000001 秒 (100 皮秒)。
人类没有任何电子探测器能像掐秒表一样,精准测量这么短的时间,从而分辨出视网膜那 10 微米的层间距。
如果不是靠“掐表”,那这台昂贵的频域 OCT (SD-OCT) 到底是靠什么知道“这一层是神经纤维层,那一层是色素上皮层”的?
答案藏在你已经掌握的那个工具里:傅里叶变换。
现在的 OCT 机器并不测量“时间”,它测量的是 “频率” (颜色)。它通过捕捉光波互相打架留下的“干涉指纹”,硬生生地从一束白光里“算”出了深度。
系好安全带。我们要把你的浏览器变成一台价值 100 万的 OCT 原型机。
1. 光谱上的“指纹”:从回声到干涉
Dr. X,还记得第 3 章我们讲的“干涉”吗?
- 波峰 + 波峰 = 增强
- 波峰 + 波谷 = 抵消
OCT 利用了一种被称为 “低相干干涉” (Low Coherence Interferometry) 的技术。
想象你发出一束包含所有颜色(波长)的宽带光(白光)。这束光被分成两路:一路射向参考镜 (Reference),一路射向病人的眼底 (Sample)。
当这两路光反射回来并在探测器上相遇时,神奇的事情发生了:
由于视网膜不同层(比如 ILM 和 RPE)的深度不同,光程差也不同。这会导致某些特定颜色的光发生“相长干涉”(变亮),而另一些颜色发生“相消干涉”(变暗)。
结果就是,探测器(光谱仪)看到了一张布满明暗条纹的 “彩虹图” (Spectrum) 。
重点来了: 这些条纹的疏密,直接编码了深度信息。
- 浅层的反射(光程差小) :会在光谱上产生 “稀疏” 的波纹(低频)。
- 深层的反射(光程差大) :会在光谱上产生 “密集” 的波纹(高频)。
这听起来是不是极其耳熟?
- 稀疏波纹(低频) $\xrightarrow{\text{傅里叶变换}}$ 近距离(浅深度)
- 密集波纹(高频) $\xrightarrow{\text{傅里叶变换}}$ 远距离(深深度)
这就是 OCT 的核心魔法:它不是在“测时间”,它是在“解乐谱”。
机器里的光谱仪拍下了这张包含复杂条纹的“乐谱”,然后电脑进行一次傅里叶变换,瞬间就把这些“条纹频率”翻译成了“深度音符”。
2. 实验 10.1:OCT 模拟器——亲手“算”出视网膜
如果不亲自试一试,这听起来就像是天方夜谭。
Dr. X,在这个实验里,我们将模拟一个最简单的视网膜模型:它只有两层(例如:内界膜 ILM 和 视网膜色素上皮 RPE)。
你的任务是:移动这两层的位置,观察 “光谱干涉图” 是如何变化的,以及傅里叶变换是如何精准地把它们“找”出来的。
(在 Wolfram Cloud 中运行以下代码)
(* 启动 SD-OCT 原理模拟器 *)
Manipulate[
Module[{k, spectrum, aScan, depth1, depth2, n = 512},
(* --- 1. 物理环境设置 (The Anatomy) --- *)
(* k 是波数 (与颜色/波长有关),模拟光谱仪接收到的宽带光源范围 *)
k = Range[0, 10, 10.0/(n - 1)];
(* 设定两层视网膜结构的深度位置 (单位: 微米) *)
depth1 = pos1; (* 第1层: 如 ILM *)
depth2 = pos2; (* 第2层: 如 RPE *)
(* --- 2. 模拟"光谱干涉信号" (The Physics) --- *)
(* 物理原理:强度 I(k) ~ 1 + cos(2 * k * depth) *)
(* 这里的 Cos 波就是光谱上的"干涉条纹"。深度越深,条纹越密 (频率越高)。*)
spectrum =
2 +
1.0 * Cos[2 * k * depth1] + (* 来自浅层 ILM 的干涉信号 *)
0.8 * Cos[2 * k * depth2] + (* 来自深层 RPE 的干涉信号 (反射率稍低) *)
RandomReal[{-0.1, 0.1}, n]; (* 模拟真实的电子噪声 *)
(* --- 3. 核心魔法:傅里叶变换 (The Algorithm) --- *)
(* 对光谱信号做 FT,这就好比"听"出和弦里的音符 *)
(* 这一步将"频域"(光谱条纹) 转换回了 "空域"(解剖深度) *)
aScan = Abs[Fourier[spectrum]];
(* Abs[]: 计算反射强度 (A-Scan 信号强度) *)
(* 我们只取前半部分数据,因为 FT 结果是对称的 *)
aScan = aScan[[1 ;; n/2]];
(* --- 4. 临床可视化面板 (The Display) --- *)
Grid[{
{Style["1. 光谱仪看到的 (原始数据)", Bold, Blue, 13],
Style["2. 电脑算出来的 (A-Scan)", Bold, Red, 13]},
{
(* 左图:光谱干涉图 (Spectrum) *)
ListLinePlot[spectrum,
PlotRange -> {0, 4}, ImageSize -> 350, AspectRatio -> 1/3,
AxesLabel -> {"波长 (颜色)", "光强"},
PlotLabel -> "干涉条纹 (Interference Fringes)",
PlotStyle -> Blue],
(* 右图:深度解算图 (A-Scan) *)
ListLinePlot[aScan,
PlotRange -> All, ImageSize -> 350, AspectRatio -> 1/3,
AxesLabel -> {"深度 (z)", "反射率"},
PlotLabel -> "视网膜断层结构 (Structural Depth)",
PlotStyle -> {Red, Thick}, Filling -> Axis]
}
}, Spacings -> {2, 1}]
],
(* --- 控制面板:你的微操台 --- *)
Style["调整视网膜层的位置 (微米)", Bold, 12],
{{pos1, 10, "第1层 (ILM) 深度"}, 5, 60, 1, Appearance -> "Labeled"},
{{pos2, 30, "第2层 (RPE) 深度"}, 5, 60, 1, Appearance -> "Labeled"},
Delimiter,
Style["\n观察指南:\n1. 深度越深,左边的条纹越密。\n2. 右边的尖峰,就是 FT 算出的解剖位置。", 10, Gray]
]
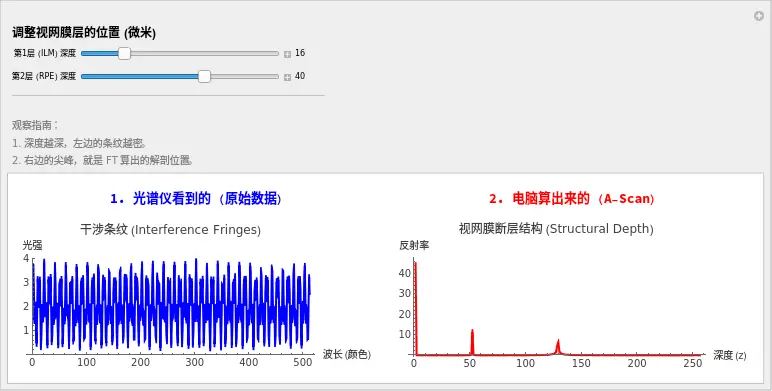
3. 见证“解密”时刻:像物理学家一样思考
Dr. X,请操作滑块,注意观察左右两张图的联动。这不仅是动画,这是每一台蔡司或海德堡 OCT 机器内部真实的运算逻辑。
场景 A:浅层结构 (模拟 ILM)
- 操作 : 将 pos1 (第1层) 拖到很小的数值(比如 5)。
- 左边(光谱图) : 你会看到一个 波浪很大、很平缓 的 Cos 曲线。这就是所谓的“低频干涉”。
- 右边(A-Scan) : 红色的尖峰紧紧贴在左侧(浅深度)。
- 洞见 : 傅里叶变换告诉我们:“在这个光谱乐谱里,我听到了一个很低沉的声音(低频)。”这意味着反射面离得很近。
场景 B:深层结构 (模拟 RPE)
- 操作: 将 pos2 (第2层) 拖到很大的数值(比如 50)。
- 左边(光谱图): 现在的波形变得 非常密集、非常刺眼,充满了细碎的锯齿。这就是“高频干涉”。
- 右边(A-Scan): 第二个红色的尖峰跑到了最右边(深深度)。
- 洞见: 傅里叶变换说:“现在我听到了一个非常尖锐的高音(高频)。”这意味着反射面离得很远。
场景 C:双层共存 (真实的视网膜)
- 操作: 让 pos1 在 15,pos2 在 40。
- 左边: 波形变得乱七八糟,不再是标准的 Cos 波,而是大浪套小浪。这就像是光谱仪“听”到了一个复杂的和弦(C大调)。
- 右边: 奇迹发生了!尽管左边的波形看起来很乱,但右边的 A-Scan 清晰地展示了 两个独立的尖峰,一个在 15,一个在 40。
- 结论: 这就是傅里叶变换的威力。它能瞬间把混合的“和弦”拆解成独立的“音符”。
4. 为什么这改变了你的临床直觉?
Dr. X,当你下次坐在那台昂贵的 OCT 机器前,看着那个像“彩虹”一样的信号强度条在跳动时,你现在的理解已经超越了 99% 的同行:
- 为什么频域 OCT (SD-OCT) 比老式的时域 OCT 快几百倍?
- 老式机器(时域): 是真的在用机械臂移动参考镜,“一点一点”地去凑深度,就像在黑暗中用手摸索。
- 现在的机器(频域): 参考镜是固定的。它通过一次拍照(光谱),然后用数学(傅里叶变换)一次性“算出”所有深度。它不是跑得快,它是算得快。
- 为什么 OCT 如此害怕“微动”?
- 因为它是靠 “干涉条纹” 来计算的。如果眼球在扫描期间发生微动(哪怕几微米),光谱上的干涉条纹就会“糊掉”(像照片拍糊了一样)。
- 一旦条纹模糊,傅里叶变换就提取不出频率,视网膜图像就会直接消失,或者出现可怕的伪影。
- 全书逻辑的闭环
- 前几章,我们用傅里叶变换分析 “横向” 的图像 (PSF, MTF)。
- 这一章,我们用傅里叶变换解析 “纵向” 的深度 (A-Scan)。
- 横向 + 纵向 = 完整的 3D 视网膜。
本章小结
- OCT 不是超声波: 它不测飞行时间,它测光谱干涉。
- 光谱是乐谱,深度是音高: 浅层反射产生稀疏条纹(低频),深层反射产生密集条纹(高频)。
- 傅里叶变换是翻译官: 它把“光谱上的条纹”瞬间翻译成“视网膜的断层”。
Dr. X,至此,我们已经完全征服了“成像”——从角膜地形图到视网膜断层。你现在拥有了分析眼球的全知视角。
但眼科医生的使命不仅是“观察”,更是“治疗”。
如果病人的晶状体坏了(白内障),你要给他换一个新的。现在的多焦人工晶体 (Multifocal IOL) 号称能让人同时看远、看中、看近。
厂家宣传册上那些精美的同心圆环,到底是什么?
为什么在塑料片上刻几个圈,就能让光线“分身”?这难道不违背能量守恒吗?
在下一章,我们将进入本书的最终篇章——手术的艺术。我们将利用衍射 (Diffraction) ——这个曾经被我们视为“敌人”(限制视力)的物理现象,把它变成设计人工晶体的超级武器。
[下一步行动]
保持上面的 Wolfram Cloud 代码打开。试着把 pos1 和 pos2 靠得非常近(例如 20 和 21)。
你会发现右边的两个尖峰开始融合,分不清彼此了。
恭喜你,你刚刚触碰到了 OCT 的 “轴向分辨率”极限 。这不取决于机器有多贵,而取决于物理学(光源的带宽)。这正是我们评判一台 OCT 好坏的终极标准。
第 11 章:衍射的“艺术”——多焦人工晶体 (IOL) 是如何工作的
致 Dr. X:
本周,你可能刚接待了一位来自人工晶体厂商的销售代表。
他递给你一本精美的小册子,封面是一个布满同心圆环、设计得像黑胶唱片一样的晶体。他兴奋地向你推销:“Dr. X,这是我们最新的全衍射三焦晶体。它利用了光的干涉原理,能在视网膜上同时创造远、中、近三个焦点。”[^5]
你礼貌地点头,但作为一名严谨的眼科医生,你的内心可能在犯嘀咕:
- 物理直觉的冲突:我们之前学的透镜(折射)都是把光聚到一个点。光怎么可能同时聚到三个地方?这难道不违背能量守恒定律吗?[^6]
- 临床现实的困惑:你的上一位植入这种晶体的病人,虽然看报纸不用戴眼镜了,但他抱怨说:“医生,我看东西是清楚,但总觉得像是透过一层没擦干净的脏玻璃 (Waxy Vision)。而且晚上开车,红绿灯周围总有一圈光晕。”[^7]
为什么“能看见”却“不透亮”?为什么会有光晕?
Dr. X,把那些宣传册扔掉。这一章,我们要用物理学来拆解这块塑料片。我们将揭示衍射光学 (Diffractive Optics) 的秘密。
你会发现,多焦晶体根本不是一个传统的“透镜”,它本质上是一个分光器 (Beam Splitter)。[^888]
1. 它是“分光器”,不是“聚光器”
还记得我们在第 3 章讲过的“波前”吗?
- 普通单焦晶体(折射型):就像一个光滑的漏斗。光线穿过它,乖乖地全部汇聚到底部(唯一的焦点)。[^9]
- 衍射多焦晶体(衍射型):它的表面刻满了细微的台阶。光线穿过它时,遇到了成百上千个微小的“棱镜”。
这里发生了神奇的事情:光不再走一条路,它被“劈”开了。[^10]
每一个台阶边缘都会引发衍射 (Diffraction)。通过精密设计这些台阶的高度 (Step Height) 和间距,我们可以强迫光波发生“相长干涉”和“相消干涉”。结果是,原本是一束的光,被强行拆成了两束(或更多)独立的波前:[^11]
- 0 级光 (Order 0):大部分光几乎不偏折,直奔远处 $\rightarrow$ 远焦点。[^12]
- 1 级光 (Order 1):一部分光被强行“弯”得更多,汇聚在近处 $\rightarrow$ 近焦点。[^13]
这就是为什么它叫“分光”。但物理学有一个残酷的定律:你不能凭空创造光。[^14]
如果你把 40% 的能量分给了“看近”,那“看远”就只剩下 60% 了(实际上更少,因为还有散射损失)。
这就是 "Waxy Vision" 的物理根源:你的病人觉得“暗”或“对比度低”,不是因为视力表看不清,而是因为视网膜上的任何一个图像,都从未得到 100% 的能量。[^15]
2. 实验 11.1:Z 轴上的舞蹈——亲手设计双焦晶体
说的再多,不如亲眼看看光是如何被“劈”开的。
在之前的章节,我们的视角一直停留在 X-Y 平面(视网膜表面)。今天,我们要切开光轴,看看 Z 轴(深度方向)上发生了什么。[^16]
Dr. X,在这个实验中,我们将把你的浏览器变成一个光路追踪实验室。我们将在一块普通的基底透镜上,叠加一个“正弦光栅”(最基础的衍射元件),看看原本单一的焦点是如何一分为二的。
注意:为了方便理解,代码中的变量名已翻译为医学术语。[^17171717]
👉 [在wolfram cloud中运行:Dr. X 的多焦晶体设计台]
(* 启动 IOL Z-轴光路模拟器 *)
Manipulate[
Module[{r, pupil, lensPhase, gratingPhase, totalPhase, zAxis, intensityCurve, maxMonoIntensity},
(* --- 1. 建立眼球模型 --- *)
(* r: 瞳孔半径, 从中心 0 到边缘 1 (归一化) *)
r = Range[0, 1, 0.005];
(* --- 2. 晶体设计工坊 --- *)
(* A. 基底透镜 (Base Lens): 负责把光聚到视网膜 (0 D) *)
(* 这里设为 0,代表一个标准的单焦晶体 *)
lensPhase = 0;
(* B. 衍射光栅 (The Grating): 模拟晶体表面刻蚀的同心圆环 *)
(* h (台阶高度): 决定了有多少光被"劈"出去 *)
(* f (圆环密度): 决定了加入度数 (Add Power) 的大小 *)
(* Cos[...] 是最基础的衍射波纹方程 *)
gratingPhase = h * Cos[f * Pi * r^2];
(* C. 组合相位: 最终植入眼内的晶体效果 *)
totalPhase = lensPhase + gratingPhase;
(* --- 3. 核心魔法:Z轴扫描 (Through-Focus Scan) --- *)
(* 我们不只看视网膜 (0D),我们扫描从远 (-1D) 到近 (+5D) 的所有空间 *)
zAxis = Range[-1, 5, 0.05];
(* --- 4. 物理计算 --- *)
(* 利用积分计算光波在 Z 轴每一点的汇聚强度 *)
intensityCurve = Map[
Function[z,
(* z * r^2 代表离焦引入的相位差 *)
(* Total[...] 模拟光波的干涉叠加。Abs^2 代表光强 *)
Abs[Total[r * Exp[I * (totalPhase + z * 2 * Pi * r^2)]]]^2
],
zAxis
];
(* 归一化: 以单焦晶体的最大亮度为标准 (100%) *)
maxMonoIntensity = Abs[Total[r]]^2;
intensityCurve = intensityCurve / maxMonoIntensity;
(* --- 5. 临床可视化面板 --- *)
Column[{
(* 上图:晶体表面设计 (侧面剖面图) *)
Style["1. 晶体表面微结构 (IOL Profile)", Bold, Blue],
Plot[h * Cos[f * Pi * x^2], {x, -1, 1},
PlotRange -> {-3.5, 3.5},
Frame -> True, FrameTicks -> {Automatic, None},
FrameLabel -> {"光瞳直径 (mm)", "相位延迟 (台阶高度)"},
ImageSize -> 400, AspectRatio -> 0.2,
Filling -> Axis, FillingStyle -> Opacity[0.3, Blue],
PlotLabel -> "微米级的台阶 (模拟剖面)"],
(* 下图:离焦曲线 (Through-Focus Curve) *)
Style["2. 视觉质量模拟 (Simulated Defocus Curve)", Bold, Red],
ListLinePlot[
Transpose[{zAxis, intensityCurve}],
PlotRange -> {{-1, 5}, {0, 1.1}},
Frame -> True,
FrameLabel -> {"屈光度 (D) \n(0=看远, 正数=看近)", "相对光强 (Energy)"},
ImageSize -> 400, ImagePadding -> {{40, 10}, {40, 20}},
GridLines -> {{0, f/2}, Automatic},
PlotStyle -> {Thick, Red},
Filling -> Axis,
Epilog -> {
(* 标注远焦点 *)
Text[Style["远焦点 (Far)", Darker[Green], 10], {0, 0.1}, {0, -1}],
(* 标注近焦点 *)
Text[Style["近焦点 (Near)", Darker[Orange], 10], {f/2, 0.1}, {0, -1}],
(* 标注能量守恒天花板 *)
Text[Style["能量守恒天花板 (100%)", Gray, Dashed], {2, 1.02}]
}
]
}, Alignment -> Center]
],
(* --- 控制面板 --- *)
Style["设计参数 (Design Parameters)", Bold, 12],
(* 参数 h: 控制能量分配 *)
(* h=0: 单焦; h=1.2: 双焦 *)
{{h, 0.0, "台阶高度 (能量分配)"}, 0, 3.0, 0.1, Appearance -> "Labeled"},
(* 参数 f: 控制加入度数 *)
(* 物理规律:圆环越密,看近越近 *)
{{f, 6.0, "圆环密度 (加入度数)"}, 2.0, 8.0, 0.5, Appearance -> "Labeled"},
TrackedSymbols :> True
]
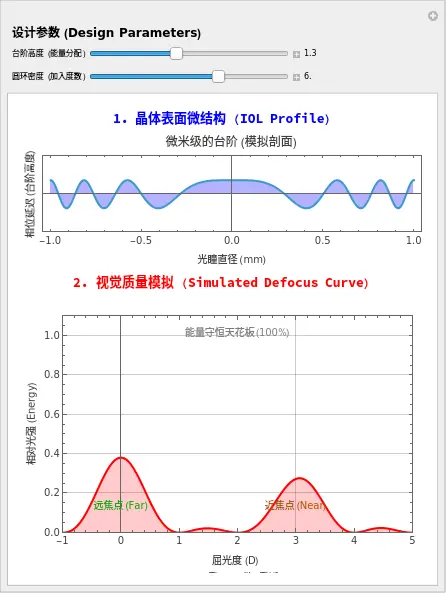
3. 见证“分身术”:如何解读实验结果
Dr. X,请按以下步骤操作。这是你理解多焦晶体物理本质、并在以后面对病人投诉时能从容解释的关键时刻。[^18]
场景 A:单焦晶体
- 操作:将台阶高度 (h) 拖到 0。
- 观察:
- 上图:一条直线。晶体表面光滑无痕。
- 下图:一个红色的巨峰,稳稳地扎在 0 (远焦点) 处。峰值达到 1.0 (100%)。
- 结论:这是标准的单焦 IOL。能量集中,对比度完美,但看近(+3.0D 处)一片漆黑。[^19]
场景 B:开启“衍射”
- 操作:慢慢增加台阶高度,直到 1.2 左右。
- 奇迹时刻:下图那个高高的红色山峰,分裂了!
- 观察:现在你有了两个峰。一个在 0(远),一个在 +3(近)。
- 结论:你刚刚在物理上制造了双焦视觉!光被强行“劈”成了两份。[^20202020]
场景 C:能量的代价
- 操作:保持在双焦状态,对比现在的峰高和场景 A 的峰高。
- 洞见:现在的两个峰,高度都只有 0.4 左右。
- 你得到了“看近”,代价是“看远”的能量从 100% 掉到了 40%。
- 剩下的 20% 去了哪里?它们变成了高阶衍射级次,散失在眼球里了。
- 这就是为什么你的病人会觉得视力表是灰的。物理定律决定了多焦晶体永远无法拥有单焦晶体的锐度。[^21]
场景 D:眩光从何而来?
- 思考:请盯着模拟图中两个峰中间的那个低谷区域。
- 原理:
- 当病人在看远处(用 0 处的焦点)时,那些原本应该汇聚在 +3 处(近焦点)的光去哪了?
- 它没有消失。它只是没聚焦。
- 它在视网膜上形成了一个巨大的、模糊的散焦光斑。这个巨大的光斑叠加在清晰的图像上,这就形成了病人所说的:“光晕 (Halo)”。[^22]
- 专家金句:看远时,近焦点就是光晕;看近时,远焦点就是光晕。这是衍射光学的原罪。你无法消除它,你只能习惯它。[^23232323]
4. 临床启示:你是光的设计师
Dr. X,经过这一章的实验,你现在的视角已经超越了普通的眼科医生。
下次当厂商代表向你展示“减少眩光”的新技术(如 Apodization,台阶渐变技术)时,你会明白他们是在做什么:他们只是试图在台阶高度上做文章,牺牲一点近视力,换取少一点的光晕。这是一场永恒的拆东墙补西墙的游戏。[^24]
但这就够了吗?
刚才我们的实验里,我们是手动调整正弦波的参数来“凑”出两个焦点的。这叫正向设计。
如果我想要三个焦点呢?如果我想要把光晕形状变成一颗爱心呢?靠手调正弦波是做不到的。
我们需要一种算法。一种能让我们画出“终点”(想要什么样的视觉),然后反向推算出晶体表面该长什么样(起点)的算法。
在下一章(也是本书的毕业设计),我们将介绍这个被称作 GS 算法 (Gerchberg-Saxton Algorithm) 的终极武器。我们将像建筑师一样,搭建属于你自己的 IOL。[^25]
[下一步行动]
保持上方的 Wolfram Cloud 代码运行。试着将台阶高度调整到一个很奇怪的数值(比如 1.8)。你会发现原来的“远、近”两个峰可能会消失,甚至出现第三个峰。这是衍射效率的非线性特性。试着找找看,有没有一个参数组合,能让中间(中距离)也能鼓起一个小包?这就是三焦晶体设计的雏形。
第 12 章:[毕业设计] IOL 积木工坊——像建筑师一样思考
致 Dr. X:
这一刻终于来了。这是您的“毕业设计”。
想象一下,您正站在全美眼科年会 (ASCRS) 最拥挤的展台前。周围人声鼎沸,您手里拿着一份刚刚发布的“连续视程”三焦晶体 (Trifocal IOL) 的技术白皮书。
图表非常精美,上面画着被称为“离焦曲线” (Defocus Curve) 的图表。您看着那几个精确隆起的小山峰,不禁陷入沉思:
“为什么是 +1.5D 和 +3.0D?为什么不是 +1.0D 或者 +2.0D?这些数字是凑巧选的,还是隐藏着什么物理学的必然?”
Dr. X,把白皮书放回展台吧。今天,我们不听别人讲故事,我们要自己动手“造”一个。
我们将揭示衍射光学设计中最高级的秘密之一:Kinoform(闪耀光栅)与倍数效应。
1. 别想复杂的算法,想想“剪影”
在上一章,我们用平滑的正弦波制造了双焦。但在现代高端晶体设计中,为了追求极致的光能利用率,我们使用的是一种更锐利、像锯齿一样的结构,学名叫做 Kinoform。
我们要如何在一个表面上同时刻出“中视力”和“近视力”两套锯齿呢?
逻辑依然是我们熟悉的“山峰轮廓”,也就是数学上的包络线 (Envelope) 原理。
想象您有两组锐利的锯齿山脉:
- 绿色山脉:代表“近视力”(+3.0D)的密集锯齿。
- 橙色山脉:代表“中视力”(+1.5D)的稀疏锯齿。
如果我们把它们重叠,阳光从正上方照下来,最终晶体表面的物理形状 (Kinoform),就是这两组山脉投下的“最大值轮廓”。
但这里有一个陷阱:如果您选错了度数,这两组锯齿就会像打架一样互相抵消,导致光能乱跑。只有选对了“倍数关系”,奇迹才会发生。
2. 实验 12.1:IOL 积木工坊
Dr. X,请坐到您的总设计师席位上。
下方的 Wolfram Cloud 代码就是您的“工坊”。
- 左图(设计图纸):显示晶体表面的相位高度。注意那些蓝色的实线,那就是您要刻在晶体上的 Kinoform 轮廓。
- 右图(临床结果):实时计算出的离焦曲线。
您的任务是:验证“倍数关系”对晶体效能的决定性影响。
👉 [在wolfram cloud中运行:Dr. X 的 IOL 积木工坊]
(* 启动 IOL 构造模拟器 *)
Manipulate[
Module[{r, totalPhase, nearAddPhase, interAddPhase, intensityAtRetina, data,
labelNear, labelInter},
(* --- 1. 定义晶体物理参数 --- *)
r = Range[0, 2, 0.02]; (* 设定晶体光学区半径 *)
labelNear = "近视力 (+" <> ToString[NumberForm[nearAdd, {2, 1}]] <> "D)";
labelInter = "中视力 (+" <> ToString[NumberForm[interAdd, {2, 1}]] <> "D)";
(* --- 2. 制造 Kinoform 积木 (相位成分) --- *)
(* Mod[...] 函数产生锐利的锯齿波,模拟衍射光栅的物理台阶 *)
nearAddPhase = If[enableNear,
(* 制造负责"看近"的密集锯齿环 *)
Mod[-(nearAdd * 2 Pi) * (r^2/4), 2 Pi],
r * 0
];
interAddPhase = If[enableInter,
(* 制造负责"看中"的稀疏锯齿环 *)
Mod[-(interAdd * 2 Pi) * (r^2/4), 2 Pi],
r * 0
];
(* --- 3. 核心魔法:包络线逻辑 (The Envelope) --- *)
(* Max[...] 模拟物理上的叠加:最终表面总是取两个光栅中"较高"的那个轮廓 *)
totalPhase = MapThread[Max, {nearAddPhase, interAddPhase}];
(* --- 4. 临床模拟:计算离焦曲线 --- *)
intensityAtRetina[defocusD_] := Module[{defocusPhase, totalWave},
(* 模拟光线穿过晶体并传播到视网膜的过程 *)
defocusPhase = (defocusD * 2 Pi) * (r^2/4);
totalWave = Exp[I * (totalPhase + defocusPhase)];
(* 计算视网膜感光细胞接收到的亮度 (Abs^2) *)
Abs[Mean[totalWave]]^2
];
data = Table[{d, intensityAtRetina[d]}, {d, -0.5, 4.0, 0.05}];
(* --- 5. 可视化布局 --- *)
Grid[{
{
(* 左栏:IOL表面设计 *)
Column[{
Style["第一步:Kinoform 表面设计 (包络线)", Bold, 13],
ListLinePlot[
{totalPhase, nearAddPhase, interAddPhase},
DataRange -> {0, 2},
PlotStyle -> {
{Blue, Thickness[0.006]}, (* 最终表面 *)
{Green, Dashed, Thin}, (* 近视力成分 *)
{Orange, Dashed, Thin} (* 中视力成分 *)
},
ImageSize -> 380, AspectRatio -> 0.25,
Filling -> {1 -> Bottom},
PlotRange -> {0, 2.2 Pi},
AxesLabel -> {"半径 (mm)", "相位高度"},
PlotLabel -> Style["注意观察:蓝色轮廓是否整齐?", Darker[Gray], 10],
PlotLegends -> Placed[{
Style["最终 IOL 表面 (Max)", Blue, Bold],
Style[labelNear, Green],
Style[labelInter, Orange]
}, Top]
],
Style["设计原理:蓝色实线总是沿着\n较高的那条虚线走 (Max逻辑)", Gray, 10]
}, Alignment -> Center],
(* 右栏:临床结果 *)
Column[{
Style["第二步:临床模拟结果 (离焦曲线)", Bold, 13, Red],
ListLinePlot[data,
PlotRange -> {{-0.5, 4.0}, {0, 1.1}},
ImageSize -> 380, AspectRatio -> 0.5,
PlotStyle -> {Red, Thickness[0.01]},
GridLines -> Automatic,
Frame -> True,
FrameLabel -> {"离焦/附加度数 (D)", "相对视力"},
PlotLabel -> "对应的视觉质量"
]
}, Alignment -> Center]
}
}, Spacings -> {1, 1}, Alignment -> Top]
],
(* --- 控制台 --- *)
Style["IOL 积木工坊:寻找完美的倍数", Bold, 12],
{{enableNear, True, "1. 添加近视力 (基准)"}, {True, False}},
{{nearAdd, 3.0, "近附加度数 (Near)"}, 2.0, 4.0, 0.25, Appearance -> "Labeled"},
Delimiter,
{{enableInter, False, "2. 添加中视力 (变量)"}, {True, False}},
(* 允许精细调整,以便观察倍数效应 *)
{{interAdd, 1.5, "中附加度数 (Intermediate)"}, 1.0, 3.0, 0.1, Appearance -> "Labeled"}
]
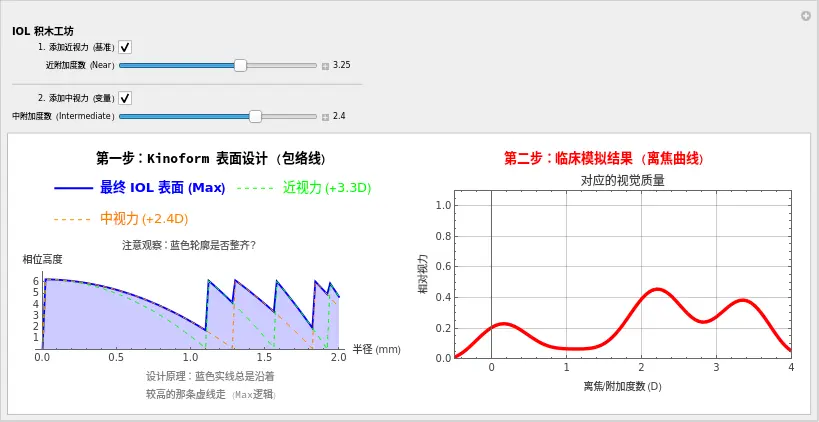
3. 见证“倍数”的魔力
Dr. X,现在我们要进行全书最关键的一次对比测试。我们将揭示为什么市面上的三焦晶体参数总是惊人地相似(例如 $+3.0\text{D} / +1.5\text{D}$ 或 $+3.5\text{D} / +1.75\text{D}$)。
场景 A:完美的和谐 (2倍关系)
- 操作:
- 勾选 "1. 添加近视力",设为 +3.0 D。
- 勾选 "2. 添加中视力",设为 +1.5 D。
- 看左图(设计图):
- 请仔细观察那条蓝色实线(最终表面)。
- 您会发现一个惊人的规律:每两个绿色锯齿(近),就刚好对应一个橙色锯齿(中)。
- 这意味着它们的边缘 (Jump) 是共用的!Kinoform 结构看起来非常有规律,就像阅兵式一样整齐。
- 看右图(临床):
- 离焦曲线非常漂亮。$0\text{D}$、$1.5\text{D}$、$3.0\text{D}$ 三个峰清晰独立,峰值很高。这就是您想要的结果。
场景 B:破坏和谐 (非倍数关系)
- 操作:
- 保持近视力 +3.0 D 不变。
- 现在,把中视力调整到一个“尴尬”的数字,比如 +2.2 D 或 +1.9 D。
- 看左图(灾难现场):
- 盯着蓝色实线。是不是觉得“乱套”了?
- 绿色锯齿和橙色锯齿不再同步。一会儿是绿线高,一会儿是橙线高。
- 由此生成的蓝色轮廓变得细碎、杂乱,充满了无意义的小台阶。这些额外的碎台阶在物理上就是散射源。
- 看右图(临床后果):
- 看看红色的曲线发生了什么?
- 峰值降低了(能量被散射掉了)。
- 峰与峰之间出现了奇怪的连粘或塌陷。
- 这就是为什么在这个参数下,病人会向您抱怨严重的“雾视感”和对比度下降。
4. 洞见:你发现了“公约数”
恭喜您,Dr. X!您刚刚独立推导出了光学工程中的 “衍射级次匹配” (Diffractive Order Matching) 原理。
厂家之所以选择 +1.5D 和 +3.0D,并不是因为病人恰好需要在 66cm 和 33cm 处看书。
而是因为 1.5 是 3.0 的一半。
在物理上,这使得近焦点的“2级衍射光”刚好能和中焦点的“1级衍射光”共用同一个锯齿边缘。
- 倍数关系 (Harmonics) = 整齐的锯齿 = 共同的边缘 = 更少的光能损失。
- 非倍数关系 = 杂乱的锯齿 = 额外的边缘 = 更多的散射和眩光。
现在,当您再次拿起那个展台上的白皮书,看到 "$+3.5\text{D} / +1.75\text{D}$" 的参数时,您不会再认为这只是视光学上的选择。您会会心一笑,因为您看到了隐藏在背后的数学之美——那是为了让 Kinoform 锯齿完美“咬合”的必然选择。
Dr. X,从第一章那个只会解 $x^2$ 的计算器,到今天利用 Max 函数和倍数原理设计出高效能的衍射晶体,您已经不仅是一个使用者,您是一个创造者。
[下一步行动]
我们的旅程即将结束,但您的探索才刚刚开始。
点击下一页,领取您的 “Dr. X 的口袋实验室”。我把前几章中那些最核心的代码——Zernike 模拟器、PSF 卷积器、以及现在的 IOL 积木工坊——都打包成了纯净版。下次再遇到推销“新一代 EDOF”的人,或者向病人解释眩光时,您可以直接用这个工具帮他验算一下:他的设计是真的创新,还是只是把锯齿弄乱了?
⚠️ 免责声明
本章提供的 Wolfram Cloud 代码及模拟结果仅用于教育演示与原理理解。代码中的模型为理想化的物理光学模型,未包含生物力学响应及个体愈合差异。严禁将本模拟结果直接用于临床诊断、手术参数设定或作为医疗器械的替代品。
终章:你就是“实验室”
致 Dr. X:
请合上那本厚厚的数学书,也把你那个写满公式的笔记本收起来吧。
此时此刻,当你读到这一页时,你已经不再是第 1 章开头那个对着 $e^{i\theta}$ 感到恐慌、担心自己能不能辅导孩子数学作业的眼科医生了。
回想一下我们要开始这段旅程时,你对“傅里叶光学”的印象是什么?是冷冰冰的积分符号?是必须死记硬背的瑞利判据?还是那些让你在学术会议上不得不假装点头的术语?
现在,看看你的手。这双手曾经只会操作裂隙灯和手术刀。但在过去的十二章里,这双手做到了物理学家做的事情:
- 在第 3 章,你像拨弄水波一样,亲手“捏”出了波前像差的形状。
- 在第 7 章,你不再被那些 Zernike 系数吓倒,而是像调音师一样,拖动滑块复现了病人的眩光。
- 在第 10 章,你用傅里叶变换破解了 OCT 的“彩虹密码”。
- 在第 12 章,你甚至像一位总工程师,利用“积木原理”设计出了属于你自己的三焦人工晶体。
你并没有变成一个数学家,你也不需要。你依然是那个治病救人的 Dr. X。但不同的是,现在的你,拥有一双能透过现象看到物理本质的“法眼”。
当别人看到一张糊烂的视力表时,你看到的是卷积。
当别人看到 OCT 上的噪点时,你看到的是频谱干扰。
当别人看到多焦晶体的广告词时,你看到的是能量分配的博弈。
1. 最后的礼物:Dr. X 的口袋实验室
在本书的最后,我不打算给你留作业。我要送给你一套武器。
在之前的每一章,为了教学,代码里包含了大量的分步演示和原理拆解。但在真实的诊室里,你没时间从头运行那些代码。你需要的是一把“瑞士军刀”——打开即用,直击问题。
下方是为你定制的“Dr. X 口袋光学实验室”。
我将全书最核心的两个功能——“像差诊断”(解释病人的视力)和“晶体模拟”(解释晶体的选择)——整合到了同一个极简界面中。
请务必将这段代码保存在你的 Wolfram Cloud 或手机书签里。它将是你职业生涯中随时调用的物理直觉。
⚠️ 免责声明
本工具及相关代码仅用于教育演示与光学原理理解。代码中的模型为理想化的物理光学模型,未包含生物力学响应及个体愈合差异。严禁将本模拟结果直接用于临床诊断、手术参数设定或作为医疗器械的替代品。
实验 13.1:终极集成——你的云端诊室
使用场景 A:诊室里的“解释神器”
病人抱怨夜间视力差,但查视力是 1.0。你无需画草图,切换到 [诊断模式],输入他的球差数值,直接让他看屏幕上的光晕:“看,这就是你晚上看到的星星,对吧?”
使用场景 B:学术会上的“测谎仪”
台上的讲者在吹嘘一款“无极变焦”晶体。你切换到 [治疗模式],简单拖动几个参数,看着离焦曲线:“嗯,原理不错,但为了景深,峰值对比度牺牲了 40%。”
👉 [在wolfram cloud中运行:Dr. X 的口袋光学实验室]
Manipulate[
TabView[{
(* --- TAB 1: 诊断模式 (像差与视觉) --- *)
"1. 诊断模式 (像差可视化)" -> Module[{
n = 128, range, xx, yy, rr, tt, aperture,
zDef, zAstig, zComa, zSph,
totalWavefront, psf, imgE, simView
},
(* 1. 铺设视网膜画布 (定义成像视野) *)
range = Range[-1, 1, 2.0/(n - 1)];
{xx, yy} = Transpose[Outer[List, range, range], {3, 2, 1}];
rr = Sqrt[xx^2 + yy^2];
(* 加微小量防止奇点,保证计算稳定性 *)
tt = ArcTan[xx + 10.^-10, yy];
(* 2. 设定瞳孔光阑 (模拟虹膜遮挡) *)
(* UnitStep: 瞳孔内为1(透光),瞳孔外为0(遮挡) *)
aperture = UnitStep[1 - rr];
(* 3. 构建 Zernike 积木 (像差零件) *)
(* Z(2,0) 离焦: 像个碗 *)
zDef = (Sqrt[3] * (2 rr^2 - 1)) * aperture;
(* Z(2,2) 散光: 像马鞍 *)
zAstig = (Sqrt[6] * rr^2 * Cos[2 tt]) * aperture;
(* Z(3,1) 彗差: 像拖尾的彗星 *)
zComa = (Sqrt[8] * (3 rr^3 - 2 rr) * Cos[tt]) * aperture;
(* Z(4,0) 球差: 像墨西哥草帽 *)
zSph = (Sqrt[5] * (6 rr^4 - 6 rr^2 + 1)) * aperture;
(* 4. 组合波前 (叠加所有像差) *)
totalWavefront = (cDef * zDef) + (cAstig * zAstig) + (cComa * zComa) + (cSph * zSph);
(* 5. 光学传输模拟 (FT) *)
(* Fourier: 让光线穿过晶状体,模拟聚焦过程 *)
(* Abs^2: 计算视网膜上感光细胞接收到的光强 (PSF) *)
psf = Abs[RotateRight[Fourier[aperture * Exp[I * 5 * Pi * totalWavefront]], {n/2, n/2}]]^2;
psf = psf/Total[Flatten[psf]]; (* 能量归一化,遵循能量守恒 *)
(* 6. 准备视力表 E *)
imgE = Rasterize[Style["E", FontFamily -> "Arial", FontSize -> 80, Bold, FontColor -> White],
ImageSize -> {n, n}, RasterSize -> {n, n}, Background -> Black];
(* 7. 核心:视觉模拟 (卷积) *)
(* ImageConvolve: 用变形的“光斑笔刷”(PSF) 重新描绘视力表 *)
simView = ImageConvolve[imgE, Image[psf]];
(* 8. 诊断面板布局 *)
Grid[{
{Style["病人的波前 (角膜/全眼)", Bold, Blue], Style["病人看到的 E (PSF卷积)", Bold, Red]},
{
(* 左图:波前地形图 *)
ArrayPlot[totalWavefront, ColorFunction -> "Rainbow", DataReversed -> True,
Frame -> False, ImageSize -> 200, Background -> Black, PlotRange -> All],
(* 右图:模拟视觉 *)
Image[simView, ImageSize -> 200]
}
}, Spacings -> {2, 1}]
],
(* --- TAB 2: 治疗模式 (晶体设计) --- *)
"2. 治疗模式 (IOL 模拟器)" -> Module[{
rIOL, nearPhase, interPhase, finalPhase,
zAxis, intensityCurve
},
(* 1. 定义晶体光学区半径 *)
rIOL = Range[0, 1.5, 0.01];
(* 2. 制造 Kinoform 积木 (相位成分) *)
(* Mod: 产生锐利的锯齿波,模拟衍射光栅的物理台阶 *)
nearAddPhase = If[enableNear, Mod[-(addNear * 2 Pi) * (rIOL^2/4), 2 Pi], rIOL * 0];
interAddPhase = If[enableInter, Mod[-(addInter * 2 Pi) * (rIOL^2/4), 2 Pi], rIOL * 0];
(* 3. 包络线原理 (Kinoform 构建) *)
(* MapThread[Max]: 模拟晶体表面的物理叠加,始终取轮廓的最高点 *)
finalPhase = MapThread[Max, {nearAddPhase, interAddPhase}];
(* 4. 离焦扫描 (模拟光在不同距离的汇聚) *)
zAxis = Range[-0.5, 4.0, 0.05];
intensityCurve = Map[Function[z,
(* Exp: 模拟光波的干涉叠加 *)
(* Abs^2: 计算成像亮度 *)
Abs[Mean[Exp[I * (finalPhase + z * 2 * Pi * rIOL^2/4)]]]^2
], zAxis];
(* 5. 治疗面板布局 *)
Column[{
Style["设计图纸 (Kinoform 相位)", Bold, Blue],
ListLinePlot[finalPhase, PlotRange -> {0, 2.2 Pi}, ImageSize -> 350, AspectRatio -> 0.2,
Filling -> Axis, PlotStyle -> Blue, Ticks -> None, Frame -> True, FrameTicks -> None],
Style["\n临床预测 (离焦曲线)", Bold, Red],
ListLinePlot[Transpose[{zAxis, intensityCurve}],
PlotRange -> {{-0.5, 4.0}, {0, 1.0}}, Frame -> True,
FrameLabel -> {"离焦 (D)", "视力/对比度"},
GridLines -> {{0, If[enableInter, addInter, None], If[enableNear, addNear, None]}, Automatic},
ImageSize -> 350, PlotStyle -> {Thick, Red}]
}, Alignment -> Center]
]
}],
(* --- 全局控制台 --- *)
Style["Dr. X 的口袋实验室", 16, Bold],
Delimiter,
(* 诊断模式参数 *)
Style["[诊断参数] 像差 (微米)", 10, Gray],
{{cDef, 0, "近视/远视 (Z2,0)"}, -0.5, 0.5, 0.05},
{{cAstig, 0, "散光 (Z2,2)"}, -0.5, 0.5, 0.05},
{{cComa, 0, "彗差 (Z3,1)"}, -0.5, 0.5, 0.05},
{{cSph, 0, "球差 (Z4,0)"}, -0.2, 0.5, 0.05},
Delimiter,
(* 治疗模式参数 *)
Style["[治疗参数] IOL 设计", 10, Gray],
{{enableNear, False, "添加近焦点"}, {True, False}},
{{addNear, 3.0, "近附加度数"}, 2.0, 4.0},
{{enableInter, False, "添加中焦点"}, {True, False}},
{{addInter, 1.5, "中附加度数"}, 1.0, 3.0},
ControlPlacement -> Left,
SaveDefinitions -> True
]
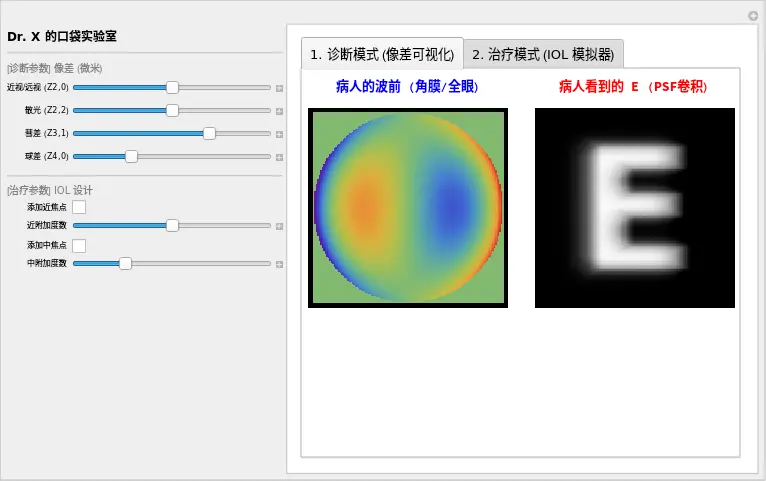
2. 真正的“治愈”
Dr. X,在本书的开头,我说过,我们不是在教书,我们是在“治愈”。
现在,你治愈了吗?
我希望你治愈的,不仅仅是对光学的恐惧,更是一种“被动接受”的职业倦怠感。
在这个技术爆炸的年代,每一天都有新的设备、新的算法、新的晶体被推送到你的面前。如果你不懂原理,你就是一个单纯的“操作员”,你会永远被厂商的宣传牵着鼻子走,你会对异常的临床结果感到无助。
但现在,你拥有了物理直觉。
你拥有了把复杂世界拆解成正弦波、再把它们重新组合起来的能力。
这不仅仅是光学的力量,这是思考的力量。
下次,当你在手术显微镜下看着那枚晶体缓缓展开,或者在电脑屏幕上看着那张五颜六色的像差图时,请记得:
那不仅仅是塑料,那不仅仅是像素。
那是光的舞蹈,那是波的干涉,那是傅里叶的魔法。
而现在,指挥棒在你的手里。
去吧,Dr. X。
去用你的“物理之眼”,看清病人的痛苦;
去用你的“口袋实验室”,设计光明的未来。
我们在云端再见。
(全书完)
