好了,终于可以开始一些公式了。
首先,我们要描述角膜的前表面,这是一个非球面,更准确的说,是一个圆锥曲线绕对称轴旋转形成的曲面。有些专利把不是球面的曲面都算作非球面,是非常不道德的行径,需要各位同道的认真鄙视。
描述圆锥曲线有很多公式,比如Douthwaite 2006, Contact lens optics and lens design一书中使用

$$
y^2=2 r_0 x - p x^2 \tag 1
$$
这个公式中,是把到镜片光轴的距离作为y,镜片上某一点到镜片中心的高度差作为x,顺便说,镜片平放时,镜片上某一点到镜片中心的高度差,叫做矢高sagittal。但这种写法要计算出矢高很麻烦,而在镜片设计时常常需要计算出矢高。
矢高有两个解,取正的那个

$$
x = (r_0+\sqrt{r0^2-p y^2})/p
$$
还有一种常见的写法,是在zemax的帮助文档里的,zemax中圆锥曲线叫做“标准面”,镜片上某一点到镜片光轴的距离写作r, 矢高写作z

$$
z = \frac{c r^2}{ 1+ \sqrt{1-(1+k)c^2 r^2}} \tag 2
$$
如果你把x->z, r->y, c-> 1/r_0, p->1+k ,然后代入一下再化简,就可以从公式2得到公式1
我个人更喜欢zemax中的写法,因为……好查,能够直接计算出矢高,而且更容易在后面加上更多的系数,形成“高次非球面”,比如“偶次非球面”
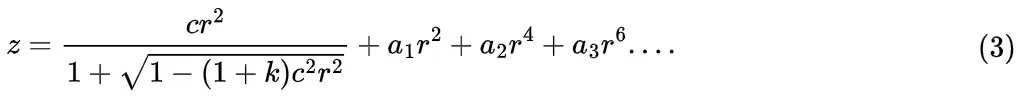
$$
z = \frac{c r^2}{ 1+ \sqrt{1-(1+k)c^2 r^2}} + a_1 r^2 + a_2 r^4 + a_3 r^6 .... \tag 3
$$
上面公式2中参数的含义是:
- c 是曲率(半径的倒数),
- r 是镜头单位下的径向坐标,
- k为圆锥系数。其中
- 圆锥系数小于-1 为双曲面,
- 等于-1 为抛物面,
- 在-1 和 0 之间为椭圆,
- 等于 0 为球面,
- 大于 0 时为扁椭圆面。
单独说一下圆锥系数。
眼科经常会用e, p, Q,在光学设计软件里可能会用k,conic。这里一次说清楚:
- Q, k, conic 是一个东西,
- p = 1+Q
- e: e是个很讨厌的东西,e的数值Q的开方,e的符号与Q相反,这在编程处理时非常非常非常^N讨厌。所以,尽量不要出现e

啊,不好意思,忘了还有一组公式。跟光学有关的。
K=337.5/R
也就是说角膜K=45D时,角膜前表面的曲率半径是7.5mm。
这个公式是:
K=(1.3375-1)/(R/1000)
也就是以毫米为单位的球面镜的屈光度计算公式。但其实角膜的折射率并非1.3375,而是1.376,这其中还有一段长长的故事,有兴趣的话,可以看我的另一篇blog《角膜的折射率》
从K=337.5/R或者R=337.5/K,我们可以得出BC弧曲率半径BCR的计算方法:
BCR= 337.5 / BC屈光度
BC屈光度 = 眼角膜的屈光度 + 需要矫正的屈光度 - 过矫正量(Jessen Factor)
比如患者(或者模拟眼)角膜前表面的曲率半径R_eye=7.5mm,患者近视Rx = -3.00D, Jessen Factor JF=0.75D
BCR= 337.5/ (337.5/ R_eye + Rx - JF) = 337.5/ (337.5/7.5 -3.00-0.75)=337.5/(45-3-0.75)=337.5/41.25=8.182 mm
公式的讲解就到这里,为了设计角膜塑形镜,我们只用两个公式,而且在使用过程中也只是整体调用,所以不必惊慌。



