Okay, we can finally start with some formulas.
First, let's describe the anterior surface of the cornea. It is a non-spherical surface, more precisely, a surface formed by rotating a conic curve around a symmetrical axis. Some patents consider any non-spherical surface as a non-spherical surface, which is highly unethical and deserves serious condemnation from fellow professionals.
There are several formulas for describing conic curves, such as the one used in Douthwaite's book "Contact Lens Optics and Lens Design" from 2006:

$$
y^2=2 r_0 x - p x^2 \tag 1
$$
In this formula, y represents the distance to the lens axis, and x represents the height difference between a point on the lens and the lens center. By the way, when the lens is placed flat, the height difference between a point on the lens and the lens center is called sagittal height. However, calculating sagittal height using this notation is cumbersome, and it is often necessary to calculate it in lens design.
Sagittal height has two solutions, and we take the positive one:

$$
x = (r_0+\sqrt{r_0^2-p y^2})/p
$$
There is another common notation found in Zemax's documentation. In Zemax, the conic curve is referred to as the "standard surface." The distance from a point on the lens to the lens axis is denoted as r, and the sagittal height is denoted as z:

$$
z = \frac{c r^2}{ 1+ \sqrt{1-(1+k)c^2 r^2}} \tag 2
$$
If we substitute x with z, r with y, c with 1/r_0, and p with 1+k, and then simplify, we can derive formula (1) from formula (2).
Personally, I prefer the notation used in Zemax because it is easier to look up, allows direct calculation of sagittal height, and facilitates the inclusion of additional coefficients for "higher-order non-spherical" surfaces, such as "even-order non-spherical" surfaces:
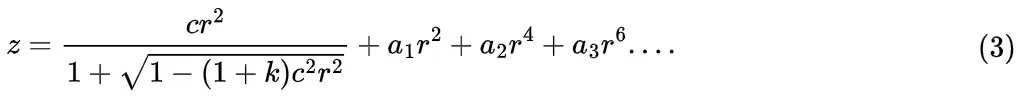
$$
z = \frac{c r^2}{ 1+ \sqrt{1-(1+k)c^2 r^2}} + a_1 r^2 + a_2 r^4 + a_3 r^6 .... \tag 3
$$
The parameters in formula (2) have the following meanings:
- c represents curvature (inverse of radius),
- r represents the radial coordinate on the lens,
- k is the conic coefficient, where:
- k < -1 corresponds to a hyperboloid,
- k = -1 corresponds to a paraboloid,
- k is between -1 and 0 corresponds to an ellipsoid,
- k = 0 corresponds to a sphere,
- k > 0 corresponds to an oblate ellipsoid.
Let's discuss the conic coefficient separately. In ophthalmology, e, p, and Q are often used, while optical design software might use k or conic. Here's an explanation to clarify their relationship:
- Q, k, and conic refer to the same thing,
- p = 1+Q,
- e: e is an annoying quantity.
Its value is the square root of Q, and its sign is the opposite of Q. Dealing with e in programming can be extremely annoying. So, it is best to avoid using e whenever possible.

Oh, sorry, I forgot about another set of formulas related to optics.
K = 337.5/R
This means that when the corneal K value is 45 D, the curvature radius of the anterior corneal surface is 7.5 mm.
The formula is:
K = (1.3375 - 1)/(R/1000)
It is a formula for calculating diopters for spherical lenses in millimeters. However, the refractive index of the cornea is not exactly 1.3375 but rather 1.376. There's a long story behind it, which you can read in my other blog post, "Refractive Index of the Cornea" if you're interested.
From K = 337.5/R or R = 337.5/K, we can derive the calculation method for the base curve radius (BCR) of a contact lens:
BCR = 337.5 / BC power
BC power = corneal power + required correction power - overcorrection (Jessen Factor)
For example, if the corneal radius of a patient's (or simulated eye's) anterior surface is R_eye = 7.5 mm, the patient's myopia is Rx = -3.00 D, and the Jessen Factor (JF) is 0.75 D:
BCR = 337.5 / (337.5 / R_eye + Rx - JF) = 337.5 / (337.5 / 7.5 - 3.00 - 0.75) = 337.5 / (45 - 3 - 0.75) = 337.5 / 41.25 = 8.182 mm
That concludes the explanation of the formulas. For designing orthokeratology lenses, we only need to use two formulas, and even then, they are used as a whole without much hassle.



