第二部分：线路之眼——流与向量场

第3章：被拉伸的地图——高度近视与移动的坐标系

“并非所有的红色都是警告，有时候，那只是地图过时了。”

3.1 引言：Dr. X 的“红色恐慌”

Dr. X 遇到了一位棘手的病人：一位 25 岁的年轻程序员，近视 900 度，眼轴长达 27.5mm。

当 Dr. X 拿到 OCT 报告时，心里“咯噔”了一下。报告上的视神经纤维层（RNFL）分析图——那个著名的“双峰图”（TSNIT 曲线）——在上方和下方区域显示出一片刺眼的红色。

机器的诊断很冷酷：视神经萎缩，疑似青光眼。

如果这发生在一位 60 岁的老人身上，Dr. X 会毫不犹豫地开始降眼压治疗。但眼前这位年轻人视野完全正常，视盘颜色红润，除了近视眼底常见的“豹纹状”改变外，看不到任何青光眼的视神经盘沿丢失。

Dr. X 陷入了两难：

• 相信机器？ 也许是极早期的青光眼，不治会瞎。
• 相信直觉？ 也许这只是高度近视造成的假象，治了就是过度医疗。
  这在临床上被称为 “红色病” (Red Disease)。这并非一种生物学上的疾病，而是一种几何学上的误会。
  本章，我们要拆开 OCT 机器的黑匣子，看看它内置的“地图”是如何在高度近视的眼球中失效的，并教你如何用数学修正它。

3.2 机器的逻辑：Jansonius 地图

OCT 机器凭什么判断哪里“变薄”了？因为它脑子里装了一张“标准地图”。这张地图大都基于同一个著名的数学模型——Jansonius 模型。

在第1章我们说过“地图不是疆域”，而在视网膜上，Jansonius 教授做了一件很聪明的事：他把弯曲的视网膜强行“铺平”了。

3.2.1 强行拉直的抛物线

如果你看过眼底照，会发现颞侧的神经纤维是弯弯曲曲的，像两道拱门避开了黄斑。但在数学处理上，处理曲线很麻烦。

Jansonius 引入了一个 “修正极坐标系”。想象一下，你把眼底照片印在一张橡胶膜上，然后抓住黄斑颞侧那个弯曲的中缝，用力把它拉直。

在这个坐标系里：

• 原本弯曲的纤维，变成了从视盘发出的直线（辐射状）。
• 数学公式：$y' = y - \text{抛物线修正项}$。
  这就像把弯曲的地铁线路图画成直的，为了方便管理。对大多数正视眼（眼轴 24mm 左右）来说，这个近似非常完美。机器在“12点钟”和“6点钟”方向寻找最厚的神经纤维，通常都能找到。

3.2.2 那个神奇的 Tanh 开关

除了拉直，神经纤维还面临一个选择：是走上方绕过黄斑，还是走下方？

Jansonius 模型用了一个双曲正切函数 (Tanh) 来描述这种分流。你可以把它想象成一个“软开关”：

• 在某个角度之前，纤维都听话地走上方。
• 在某个临界点（大约 $121^\circ$），纤维突然收到信号，全部转向去走鼻侧。
  这构成了标准地图的骨架。但问题是，这副骨架是死板的。

3.3 当疆域被拉伸：高度近视的几何灾难

现在，让我们看看那位年轻程序员的眼睛。

他的眼球不是球体，而是一个被拉长的椭球体（橄榄球）。眼轴从 24mm 变成了 27.5mm。这种拉伸不是均匀的，眼球后极部 (Posterior Pole) 被撑得最大。

3.3.1 车站移动了，车还在原地等

想象一下，如果把上面那个“橡胶膜地图”用力向左右拉伸，会发生什么？

1. 物理位移：原本位于视盘正上方（12点钟方向）的神经纤维束，会被物理力量拖拽向颞侧（耳朵方向）。
2. 角度偏移：原本在 $90^\circ$ 的山峰，现在可能移到了 $70^\circ$。
3. 拥挤效应：上下方的纤维束向中间靠拢，夹角变小了。
   这就是 “颞侧偏移” (Temporal Shift)。

3.3.2 误诊的诞生

回到 OCT 机器的视角。它是一个只懂查表的傻瓜。

它拿着“标准地图”，依然固执地去 12点钟 方向找神经纤维。

但因为高度近视的拉伸，那里的神经纤维已经搬家去了 10点钟 方向。

机器在 12 点钟摸了个空，发现厚度变薄了，立刻报警：“红色警报！神经萎缩！”

而在 10 点钟方向，机器可能会测得异常的厚度，但它往往选择忽略，或者以为是别的变异。

结论： 病人没有病，是机器在错误的地方寻找正确的东西。

3.4 修正坐标系：给地图加个“近视滑块”

既然知道了原因，作为“空间的架构师”，Dr. X 不应该扔掉 OCT，而应该修正它。

我们不需要极其复杂的物理模型，只需要在 Jansonius 的公式里加一个 “眼轴修正项”。

我们引入一个参数 $\delta(AL)$（漂移角），它与眼轴长度 (AL) 成正比。根据临床大数据（Yamashita 等人的研究），眼轴每增长 1mm，神经纤维峰值大约向颞侧移动 $2.5^\circ$。

修正后的逻辑很简单：

对于那位眼轴 27.5mm 的患者，修正量是：

这意味着，Dr. X 在看 OCT 时，要把脑子里的刻度盘向颞侧旋转 $10^\circ$。

3.5 计算眼科学实战：Wolfram 测谎仪

光说不练假把式。我们用 Wolfram Language 写一个小程序，模拟这种“颞侧偏移”。Dr. X 可以输入病人的眼轴，直观地看到神经纤维是如何“搬家”的。

ClearAll["Global`*"]

(* 第3章 V3.0：基于连续函数的稳健型模拟器 *)
(* 核心改进：弃用 ListLinePlot，改用 Plot 直接绘制数学函数，杜绝数据生成环节的 Bug *)

Manipulate[
 Module[{gaussianFunc, currentShift, currentPeak, isRisk},
  
   (* 1. 定义数学模型：连续的高斯函数 *)
   (* 这种写法比 Table 生成列表更稳定，不会因为计算延迟而丢帧 *)
   gaussianFunc[t_, peak_] := 100 * Exp[-0.5 * ((t - peak)/15.0)^2] + 50;
   
   (* 2. 实时计算位置 *)
   currentShift = If[AL > 23.5, 2.5 * (AL - 23.5), 0];
   currentPeak = 90 - currentShift;
   isRisk = (AL > 26.0); (* 风险阈值判断 *)

   (* 3. 绘图输出 *)
   Show[
    (* 图层1：标准正视眼 (灰色虚线) *)
    Plot[gaussianFunc[x, 90], {x, 0, 180},
     PlotStyle -> {Thickness[0.006], Dashed, Gray},
     Filling -> Axis, FillingStyle -> Opacity[0.1, Gray],
     PlotRange -> {{0, 180}, {0, 200}}
    ],

    (* 图层2：患者实测 (动态实线) *)
    (* 使用 Plot 直接渲染函数，确保曲线永远存在 *)
    Plot[gaussianFunc[x, currentPeak], {x, 0, 180},
     PlotStyle -> {Thickness[0.008], If[isRisk, Red, Darker[Green]]},
     Filling -> Axis, FillingStyle -> Opacity[0.2, If[isRisk, Red, Green]]
    ],
    
    (* 图层3：辅助标注 *)
    Graphics[{
      (* 动态箭头：只有发生偏移时才显示 *)
      If[currentShift > 0.1, 
       {Blue, Arrowheads[0.03], Arrow[{{90, 160}, {currentPeak, 160}}]}, 
       Nothing
      ],
      
      (* 垂直参考线：机器检测的位置 *)
      {Dashed, Lighter[Gray], Line[{{90, 0}, {90, 200}}]},
      
      (* 文本标注 *)
      Text[Style["Standard (12 o'clock)", Gray, 10], {90, 190}],
      If[currentShift > 0.1,
        Text[Style["Temporal Shift: " <> ToString[NumberForm[currentShift, {3, 1}]] <> " deg", Blue, 12, Bold], 
        {(90 + currentPeak)/2, 175}],
        Nothing
      ]
    }],

    (* 界面设置 *)
    Frame -> True,
    FrameLabel -> {"Position (Degrees)", "RNFL Thickness (um)"},
    GridLines -> {{90}, Automatic},
    GridLinesStyle -> Directive[LightGray, Dashed],
    ImageSize -> 500,
    (* 使用英文标题避免乱码 *)
    PlotLabel -> Style["Dr. X's Myopic Shift Simulator", 18, Bold, FontFamily -> "Helvetica"]
   ]
 ],
 
 (* 交互滑块 *)
 {{AL, 23.5, "Axial Length (mm)"}, 22.0, 30.0, 0.1, Appearance -> "Labeled"},
 TrackedSymbols :> {AL}
]

3.5.1 代码解读

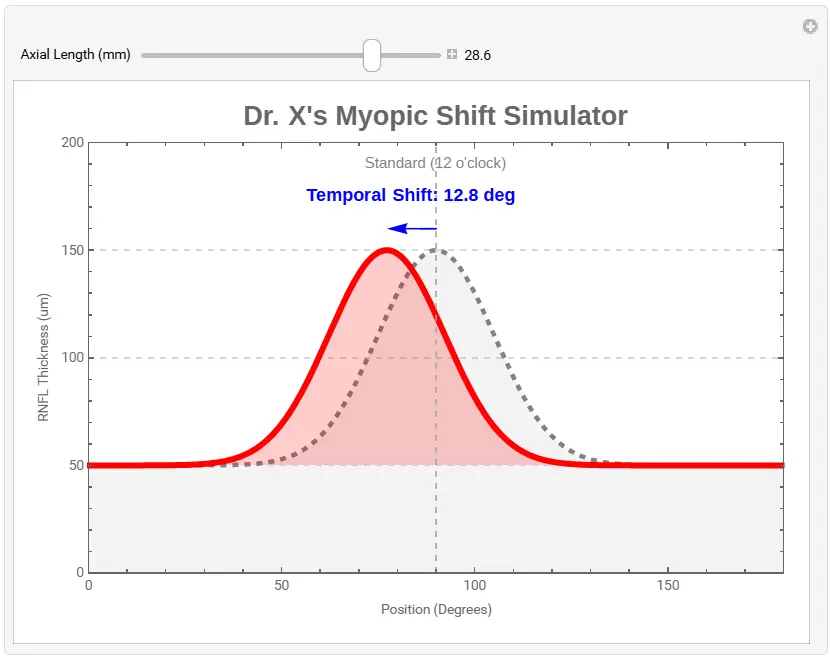
运行这段代码，试着拖动“眼轴长度”的滑块：

1. 当 AL = 23.5mm（标准）时：红色曲线（患者）与灰色阴影（数据库标准）完美重合。机器显示绿灯。
2. 当 AL = 28.0mm（高度近视）时：红色曲线明显 向左（颞侧）移动。
   • 请注意 $90^\circ$（12点钟） 的位置：灰色的标准告诉机器这里应该很厚，但红色的实测线在这里已经开始下降了。
   • 结果：机器测到的厚度 < 标准厚度 -> 报红（误诊）。
   • 真相：厚度峰值并没有消失，它只是移到了 $78^\circ$ 左右。

3.6 结语：从“看红”到“看峰”

Dr. X，现在你可以更自信地回复那位年轻的程序员了。

你不需要因为那片红色的区域而惊慌。你需要做的是：

1. 看眼轴：确认是否属于高度近视。
2. 看峰值：在 TSNIT 曲线图上，用你的肉眼去找那个波峰。如果波峰虽然移位了，但依然高耸、完整，那么他很可能只是“被拉伸了”，而不是“萎缩了”。

Jansonius 模型是伟大的，但它是静态的。在高度近视日益流行的今天，我们需要一个动态的坐标系。

但在这一切的背后，还有一个更深层的问题：神经纤维 为什么 要向颞侧移动？这种移动仅仅是机械拉伸吗？还是说，神经纤维在生长时，就像聪明的蚂蚁一样，在寻找一条 最省力 的路径？

在下一章，我们将从单纯的“拉伸地图”，进阶到 “寻找路径”。我们将引入物理学中最优美的原理—— 最小作用量原理 ，看看神经纤维是如何在弯曲的视网膜上冲浪的。

第4章：最小作用量路径——为何视神经要绕路？

“自然界不做无用功。若要从 A 点到 B 点，光线选择时间最短的路，而生命选择能量最省的路。”

—— 皮埃尔·德·费马 (Pierre de Fermat)

4.1 引言：优雅的弓形束

Dr. X，请回想一下教科书上那张经典的视网膜神经纤维层（RNFL）走行图。

视神经纤维从视网膜周边出发，汇聚向视盘。但在黄斑 (Macula) 附近，它们并没有走直线，而是优雅地绕了一个大弯，形成了特征性的 “弓形束” (Arcuate Bundles)。正是这两个弓形区域，构成了青光眼视野缺损最常见的“Bjerrum 暗点”。

你是否想过：为什么它们要走弯路？

传统的解释是：“为了避开黄斑中心凹，保证视力敏锐度。” 这没错，但这对我们预测病理没有帮助。

在上一章，我们发现高度近视会“拉伸”地图；而在这一章，我们要探讨的是 “路径的选择”。

目前的临床金标准（Jansonius 模型）是通过统计大量正常人的眼底，画出了一堆数学曲线来拟合这个形状。但这就像是用圆规去描摹叶子的形状——你画得很像，但你不知道叶子为什么长这样。

今天，我们要换一种思路。我们不“描摹”路径，我们来 “生长”路径。我们将利用微分几何中的 测地线 (Geodesic) 概念，重现大自然在胚胎发育期所做的选择。

4.2 蚂蚁、高山与能量场

为了理解视神经的逻辑，请想象一只微小的蚂蚁（神经轴突的生长锥），它要从视网膜的颞侧爬回视盘（家）。

4.2.1 规则一：懒惰是美德（最小作用量原理）

这只蚂蚁非常“懒”，或者说非常高效。它永远通过消耗最少能量的路径回家。

• 在平地上，最省力的路是直线。
• 在球面上，最省力的路是大圆弧（就像飞机的航线）。
  在微分几何中，这条“最省力”的路径，就叫做测地线。

4.2.2 规则二：黄斑是一座高山（势能场）

现在的视网膜不再是一张平纸，也不仅仅是一个球。在蚂蚁的感知中，黄斑中心凹不是一个坑，而是一座难以翻越的高山（生物排斥力场）。

之所以这么说，是因为在分子生物学层面，黄斑区会分泌 Slit/Robo 等排斥性导向因子。这在数学上等价于一个高耸的高斯势垒 (Gaussian Potential Barrier)。

4.2.3 决策时刻

当蚂蚁走到黄斑颞侧时，它面临两个选择：

1. 直穿黄斑：路程虽短，但要翻越高山，累死（能量成本极高）。
2. 绕行：路程变长了，但地势平坦，轻松（能量成本低）。
   聪明的蚂蚁选择了绕行。于是，弓形束诞生了。
   不是有人画出了弓形，而是 能量场（地形）+ 最小作用量原理（规则） 自然涌现出了弓形。

4.3 计算眼科学实战：Wolfram 虚拟轴突追踪器

Dr. X，不需要复杂的微分方程，我们用 Wolfram Language 来模拟这个“蚂蚁寻路”的过程。

我们将构建一个 “虚拟轴突追踪器”。你只需要告诉程序黄斑和视盘在哪里，它就能自动为你生成视神经的走行图。

代码解读

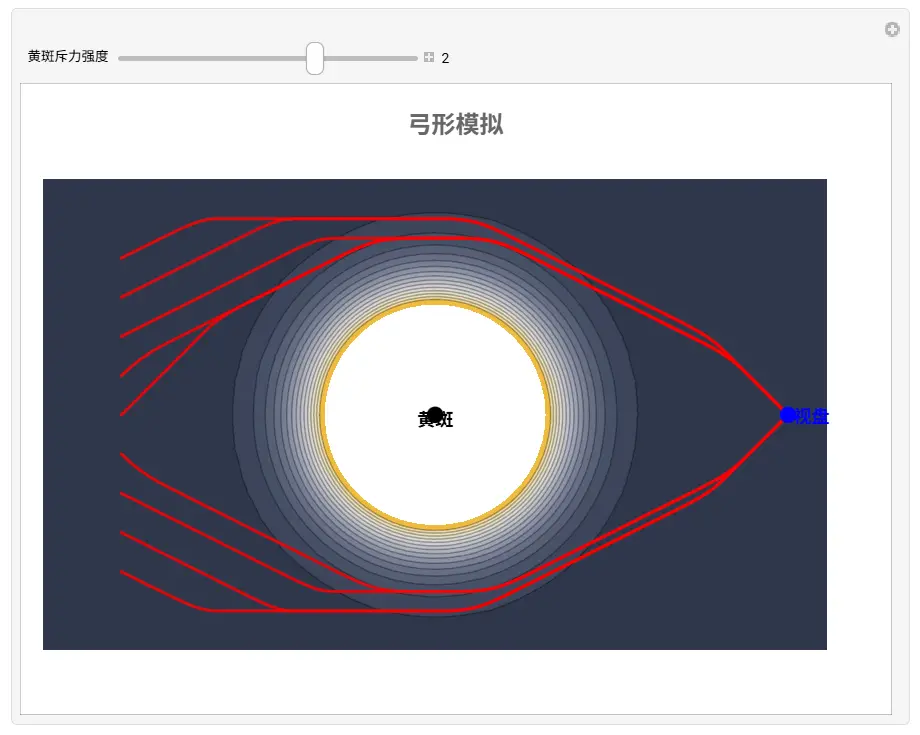
当你运行这段代码时，你会看到神奇的一幕：

我们并没有命令线条画成弓形，但红色的线条为了避开中间那个虚线标示的“黄斑高能区”，自动弯曲成了完美的上下弓形束。

这就是 计算眼科学 的魅力：我们输入的是物理规则，输出的是解剖结构。

4.4 临床启示：当能量场发生改变

这个模型对临床有什么用？它能解释许多静态地图无法解释的现象。

4.4.1 颞侧中缝：不是一条线，是一个分水岭

在解剖书上，颞侧中缝 (Temporal Raphe) 是一条将上下视网膜分开的水平线。

但在我们的模型中，它是 能量的分水岭。

想象雨水落在山脊上，往左流还是往右流？这取决于山脊的微小倾斜。

• 正常人：黄斑和视盘位置相对水平，中缝也是水平的。
• 变异：如果患者的视盘比黄斑位置高 (Fovea-Disc Angle 较大)，能量场就倾斜了。所有的“雨水”（神经纤维）路径都会发生偏转。
  临床痛点：这就是为什么有些青光眼患者的视野缺损位置很奇怪，不符合标准的纳斯特阶梯 (Nasal Step)。因为 他们的中缝本来就是歪的。用我们的模型，你可以根据患者特有的黄斑位置，计算出他专属的中缝位置，从而精准对应视野缺损。

4.4.2 高度近视：被拉伸的跑道

当眼轴变长，后巩膜葡萄肿形成时，不仅距离变了，地形的曲率 (Curvature) 也变了。

我们在第2章学过，负曲率（马鞍面）会发散测地线，正曲率（凸面）会汇聚测地线。

高度近视眼底往往由复杂的曲率构成。神经纤维在经过葡萄肿边缘时，会被地形“折射”。

结论：高度近视患者的 RNFL 变薄，有时不是因为神经死了，而是因为地形变了，神经纤维 换了一条路走，导致原本该厚的地方变薄了。

4.5 结语：从查表员到建筑师

Dr. X，传统的医生像是一个 “查表员”：拿着一张标准地图（Jansonius 图），去比对每一个病人。如果病人长得和地图不一样，就认为是病态。

而掌握了微分几何的你，现在是一位 “空间的架构师”。

你知道视网膜上的线条不是画上去的，而是 “流” 出来的。

• 黄斑是石头，视盘是下水道口。
• 神经纤维是水流。
  如果石头挪了位置（解剖变异），水流自然会改道。
  如果地面塌陷了（葡萄肿），水流自然会分散。
  理解了 “最小作用量原理”，你就拥有了预测这些变化的超能力。你不再被红色的误报所欺骗，因为你能看穿那些弯曲路径背后的物理必然。
  在下一章，我们将把这个二维的“流”，升级为三维的“通量”。我们将探讨一个更深刻的问题：当视网膜变薄时，视野为什么还是好的？（最优传输与通量守恒）。

第5章：最优传输——光流的守恒

“水之形，避高而趋下。神经之行，避耗而趋简。”

5.1 引言：消失的轴突去哪了？

Dr. X，让我们回到诊室，面对那个令所有眼科医生头疼的瞬间。

你面前坐着一位高度近视的患者。他的 OCT 报告上，视盘颞侧的神经纤维层（RNFL）厚度显示为刺眼的红色——“变薄”。

机器的逻辑很简单：正常人这里有 80 微米厚，他只有 50 微米，所以他“萎缩”了，他有青光眼。

但是，他的视野检查 (Visual Field) 却是完全正常的“白板”。

你陷入了沉思：

• 是视野检查不够灵敏？（潜伏期？）
• 还是 OCT 机器在撒谎？
  实际上，轴突并没有消失，它们只是 “摊薄” 了。
  想象一条河流。当河道变宽时，水位自然会下降。水流的总量（通量）并没有减少，只是承载它的容器变大了。
  在高度近视眼中，眼球后极部的扩张就像河道变宽。如果我们只盯着“水位”（厚度）看，就会误以为水干了。
  本章，我们将引入物理学中的 “连续性方程”和“最优传输理论”，不再看静态的“厚度”，而是去计算动态的“通量”。我们将学会区分：什么是病理性的枯竭，什么是物理性的流淌。

5.2 物理直觉：从“画线”到“流体”

在上一章，我们把神经纤维比作爬山的蚂蚁。这一章，为了处理数量巨大的轴突（100万根），我们需要把它们看作一种流体。

5.2.1 连续性方程：生物界的守恒律

不用担心复杂的数学符号，连续性方程 (Continuity Equation) 翻译成临床语言只有一句话：

在一个封闭系统中，如果不发生凋亡（青光眼），流入的轴突数量必须等于流出的数量。

数学表达式简化版：

5.2.2 破解“红病”的密码

让我们用这个公式来审视高度近视眼：

• 正视眼：视盘周围的巩膜环较小（周长 $C$）。为了容纳 100 万根轴突，需要的厚度是 $T$。
• 高度近视：眼球被拉长，巩膜环被撑大，或者因为光学放大率效应，我们扫描的圆周长变成了 $2C$。
  根据守恒律：
  
  $$C \times T = 2C \times \text{新的厚度}$$
  
  为了维持等式平衡，新的厚度必须变成 $T/2$。
  结论：
  OCT 报告上的“变薄”，往往不是病。那是生物体为了适应眼球扩张，必须遵循的物理铁律。
  Dr. X，下次看到单纯的 RNFL 变薄时，请先计算一下他的眼轴。如果是长眼轴，那多半只是“河面宽了，水浅了”，而不是“水源枯竭了”。

5.3 动态分水岭：颞侧中缝的秘密

解决了“量”的问题，我们再来解决“方向”的问题。

视网膜上有一条隐形的线，叫做颞侧中缝 (Temporal Raphe)。它位于黄斑的颞侧，是上、下神经纤维束的分界线。

• 中缝以北的轴突，汇入视盘上方。
• 中缝以南的轴突，汇入视盘下方。

5.3.1 屋脊上的雨水

把黄斑颞侧的区域想象成一个屋脊。

雨水（轴突）落在屋脊上，是流向北坡还是南坡，完全取决于屋脊的倾斜角度。

传统的教科书（和 Jansonius 模型）假设所有人的屋脊都是水平的。

但在临床中，有些人的视盘长得高一点，有些人的眼球发生了外旋。这导致“屋脊”发生了倾斜。

5.3.2 为什么视野缺损对不上？

这就是为什么你经常遇到 “结构-功能不匹配” 的第二个原因：

• OCT 显示视盘下方有缺损。
• 根据教科书，这应该对应视野的上方缺损。
• 但病人的视野缺损却跑到了鼻侧水平线附近，甚至跨过了中线。
  原因： 这个病人的中缝根本不是水平的！他的“屋脊”是歪的，导致原本属于“下方”的雨水，实际上流到了“上方”的管道里。
  利用最优传输理论 (Optimal Transport)，我们可以根据视盘和黄斑的相对位置，计算出每个人独特的 “动态中缝”。这不是一条画在纸上的死线，而是一个随地势而变的分水岭。

5.4 计算眼科学实战：Wolfram 流体模拟器

Dr. X，不需要做复杂的计算。我们可以编写一段 Wolfram 代码，为你生成每一只眼睛专属的“轴突流场图”。

这段代码的核心逻辑是：

1. 建立地形：把视网膜看作一个流形。
2. 设定引力和斥力：视盘是吸水的洞（引力），黄斑是挡水的石（斥力）。
3. 让水流淌：模拟轴突寻找阻力最小的路径。

ClearAll["Global`*"]

(* 第5章 5.4 极速版：性能优先的流场模拟 *)
(* 核心修正：
   1. 移除 StreamColorFunction，改用纯色，防止云端渲染超时导致"白板"。
   2. 手动推导梯度公式，替代 Grad 符号计算，大幅提升响应速度。
   3. 降低采样密度至"中等"，确保流畅度。
*)

Manipulate[
 Module[{
   foveaPos = {0, 0},
   discPos = {4.5, discY},
   (* 变量声明 *)
   sinkVector, obstacleVector, totalFlow, rapheAngle
   },

  (* 1. 物理引擎：直接写出向量公式 (硬编码) *)
  
  (* 汇 (视盘): 向量指向视盘中心，强度随距离衰减 *)
  (* 类似于引力场: v = -(p - center) / |dist|^2 *)
  sinkVector[pt_] := -1.5 * Normalize[pt - discPos] / (EuclideanDistance[pt, discPos] + 0.5);

  (* 障碍 (黄斑): 向量背离黄斑中心 *)
  (* 高斯势场的梯度: v = (p - center) * Exp[...] *)
  obstacleVector[pt_] := 2.0 * (pt - foveaPos) * Exp[-2.0 * Norm[pt - foveaPos]^2];

  (* 总流场 = 汇的吸力 + 山的斥力 *)
  totalFlow[pt_] := sinkVector[pt] + obstacleVector[pt];
  
  (* 2. 计算中缝几何角度 *)
  rapheAngle = ArcTan[discPos[[1]], discPos[[2]]] / Degree;

  (* 3. 极速绘图 *)
  Show[
   StreamPlot[
    totalFlow[{x, y}], {x, -4, 6}, {y, -3, 3},
    
    (* 核心修改：使用纯色线条，确保可见性 *)
    StreamStyle -> Directive[Orange, Opacity[0.8], Thickness[0.004], Arrowheads[0.03]],
    StreamPoints -> Automatic, (* 自动采样，不强求 Fine *)
    PerformanceGoal -> "Speed", (* 告诉系统：快比好看重要 *)
    AspectRatio -> Automatic
   ],

   (* 辅助标记 *)
   Graphics[{
     (* 视盘 *)
     {Blue, Disk[discPos, 0.2], Text[Style["视盘", White, Bold], discPos]},
     (* 黄斑 *)
     {Black, Disk[foveaPos, 0.15], Text[Style["黄斑", Black, Bold], foveaPos, {0, 1.8}]},
     (* 动态中缝指示线 *)
     {Red, Dashed, Thickness[0.006], 
      Rotate[Line[{{-4, 0}, {0, 0}}], rapheAngle Degree, {0, 0}]}
   }],

   Frame -> True, FrameTicks -> None,
   PlotRange -> {{-4, 5.5}, {-3, 3}},
   ImageSize -> 550,
   PlotLabel -> Style["最优传输：视盘位置对中缝的影响", 16, Bold, FontFamily -> "Helvetica"]
  ]
 ],
 
 (* 交互滑块 *)
 {{discY, 0, "视盘垂直位置 (mm)"}, -2.0, 2.0, 0.1, Appearance -> "Labeled"},
 TrackedSymbols :> {discY} (* 只追踪 y 轴变化，防止不必要的重算 *)
]

代码看点

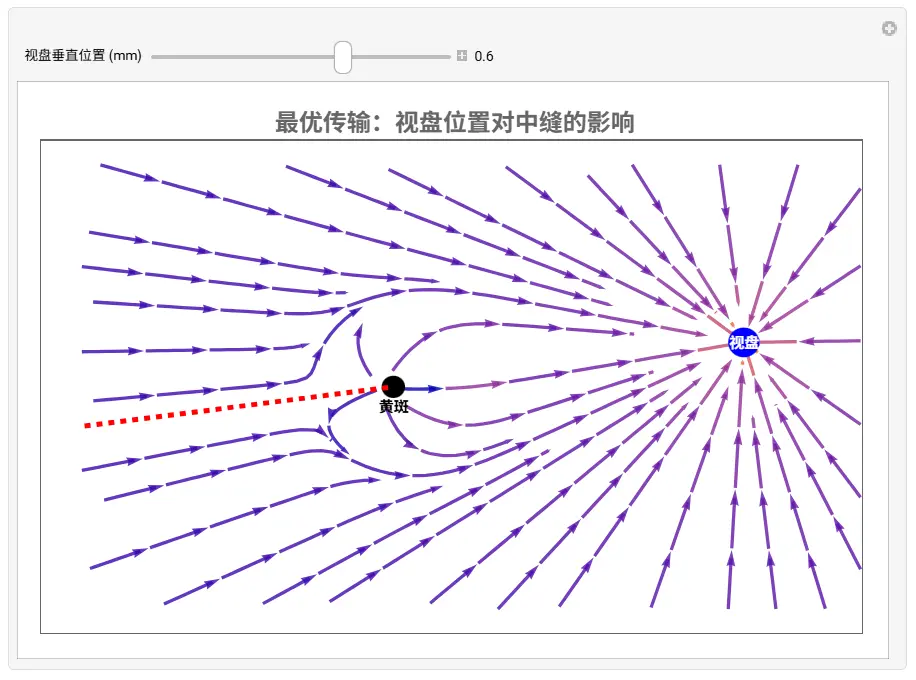
运行这段代码，你会看到：

• 橙色的线条（轴突）像水流一样，优雅地绕过中间红色的黄斑。
• 在黄斑左侧（颞侧），你会看到明显的 分流现象 ——这就是中缝。
• 尝试修改 discPos 的坐标（例如改成 {1.5, 0.5}），你会发现那条虚线所示的分水岭也随之发生了旋转。 这就是个性化诊断的威力。

5.5 结语：从观察者到架构师

第5章的核心任务，是帮助你建立一双 “透视眼”。

当你再次面对一张红色的 OCT 报告时，请不要只看到“变薄”。

• 用 连续性方程 去思考：这是不是因为河道变宽了？
• 用 最优传输 去思考：这是不是因为水流改道了？
  Dr. X，你不再是被机器报警声吓得手忙脚乱的操作员。你是理解了光流守恒定律的空间架构师。你知道，有时候红色不是警告，它只是大自然在不同的几何表面上，为了守恒而做出的妥协。
  在下一章，我们将离开视网膜，去探索一个更令人着迷的领域—— 渐进多焦点镜片。我们将用几何学解释，为什么完美的镜片是不存在的，以及如何与必须存在的像散共舞。