第三部分：屈光景观——像差与曲率

第6章：闵克维茨定理——像散的代价

“像散为了让平滑变焦成为可能，而必须支付的几何税。”

6.1 引言：寻找“独角兽”

Dr. X，你的诊室里一定出现过这样的场景：

一位刚步入老视年纪的成功人士坐在裂隙灯前，他对眼镜寄予了厚望：“大夫，钱不是问题。我要最好的镜片。我要看远处的路牌清楚，看手里的股票行情也清楚；中间过渡要像年轻时一样顺滑，而且——最重要的是——我不希望转头时旁边有任何变形。”

你很想满足他，你翻遍了 Zeiss、Essilor、Hoya 的顶级产品目录，看到了无数华丽的术语：“全视野”、“无盲区”、“黄金宽通道”。

但作为 “空间的架构师”，你心里清楚：他想要的这种镜片，在几何上是不存在的。就像你无法画出一个既是圆形又是方形的图形一样。

这章的任务，不是让你去跟患者讲数学，而是给你一样武器——闵克维茨定理 (Minkwitz Theorem)。它将帮你粉碎商业营销的泡沫，让你理直气壮地告诉患者：像散不是工艺的瑕疵，它是几何的法则。

6.2 物理直觉：被撕裂的橘子皮

在引入公式之前，我们先做一个思想实验。

6.2.1 为什么必须有像散？

想象你手里有一块平整的橡皮膜（代表 $0$ 度的平光镜）。

看远：上半部分保持平整。
看近：下半部分，你需要把它弄“鼓”起来（增加正球镜度数，Add）。
过渡：你必须在这两者之间建立一个平滑的斜坡。
试着做一下。当你把下半部分强行撑起来，同时保持中间连接处平滑时，你会发现侧面必然会起皱褶。
这就是 高斯绝妙定理 (Theorema Egregium) 的通俗版：

光焦度 (Power) 是我们想得到的“隆起”。
像散 (Astigmatism) 是侧面被迫产生的“皱褶”。
在黎曼流形上，你不可能只改变经线（垂直）方向的曲率，而不引起纬线（水平）方向的扭曲。像散，就是为了维持表面连续性而必须支付的 “几何税”。

6.3 核心定律：惩罚系数

1963年，数学家 Günter Minkwitz 发现了一个让所有镜片设计师绝望的规律。不用担心微积分，这个公式翻译成人话非常简单。

6.3.1 闵克维茨公式

在渐进片中间那条狭窄的“清晰走廊”上，像散的变化遵循以下铁律：

\text{像散的变化速度} \approx 2 \times \text{度数增加的速度}

写成数学符号就是：

\frac{\partial A}{\partial x} \approx 2 \frac{\partial P}{\partial y}

右边 ( $\frac{\partial P}{\partial y}$ )：代表通道设计。如果通道很短，度数这就必须在短距离内急剧增加，这个值就很大。
左边 ( $\frac{\partial A}{\partial x}$ )：代表视野宽窄。这个值越大，意味着你视线稍微往旁边一偏（ $x$ 方向），像散就疯涨，视野就越窄。
中间的 $2$ ：这是惩罚系数。

6.3.2 临床翻译

Dr. X，这个公式告诉你三个残酷的事实：

短通道 = 窄视野：如果你为了配合时尚小镜框，选了短通道（度数变化快），那么侧边的像散会以 2 倍 的速度恶化。
高 Add = 窄视野：老花度数越高 (Add 大)，度数爬坡越陡，旁边的像散“悬崖”就越深。
没有奇迹：除非厂商能打破黎曼几何，否则凡是宣称“短通道且全视野”的广告，都是在撒谎。

6.4 计算眼科学实战：Wolfram 验光师助手

让我们写一段简单的 Wolfram 代码，把这个抽象的定理变成你手边的 “处方风险评估器”。我们将计算特定处方下的像散梯度。

(* --------------------------------------------------------- *)
(*   程序名称：Smooth-Flow PAL Topographer (流体渐进地形生成器)   *)
(*   版本：V3.0 (去伪影/平滑化版)                               *)
(*   改进：使用 Sigmoid 函数替代分段函数，模拟真实抛光表面         *)
(* --------------------------------------------------------- *)

ClearAll[SimulateSmoothPAL];

SimulateSmoothPAL[addPower_, corridorLen_, designType_] := Module[
    {
        (* 空间参数 *)
        yMax = 20, yMin = -20, xMax = 20,
        
        (* 1. 几何骨架：使用平滑插值构建清晰区边界 *)
        (* 这是一个连续的样条曲线，没有任何折点 *)
        boundaryCurve, 
        
        (* 2. 物理场：硬度系数分布 *)
        stiffnessField,
        
        (* 3. 最终像散函数 *)
        astigFunction,
        
        (* 绘图变量 *)
        minWidth, startY, endY, plot
    },

    (* 定义关键节点 *)
    startY = 4; (* 通道入口 *)
    endY = startY - corridorLen; (* 通道出口 *)
    
    (* 闵克维茨理论宽度 *)
    minWidth = 0.5 / (2 * (addPower / corridorLen));
    
    (* --- 核心改进 A: 连续的边界函数 --- *)
    (* 使用 Spline (样条) 确保导数连续，没有棱角 *)
    boundaryCurve = Interpolation[{
        {yMax, 35},                (* 远用极宽 *)
        {startY + 4, 15},          (* 远用过渡 *)
        {startY, 6},               (* 漏斗口 *)
        {(startY + endY)/2, minWidth}, (* 最窄腰部 *)
        {endY, minWidth * 1.5},    (* 出口扩张 *)
        {yMin, minWidth * 5.0}     (* 近用大视野 *)
    }, Method -> "Spline", InterpolationOrder -> 3];

    (* --- 核心改进 B: 连续的硬度场 --- *)
    (* 不再使用 If/Piecewise。使用 LogisticSigmoid 实现柔和过渡 *)
    (* 远用区硬度低(0.2)，通道区硬度高(2.5)，近用区硬度中(1.0) *)
    stiffnessField[y_] := Module[{s1, s2},
        (* s1: 从远用到通道的过渡开关 *)
        s1 = LogisticSigmoid[-(y - startY)*2]; 
        (* s2: 从通道到近用的过渡开关 *)
        s2 = LogisticSigmoid[-(y - endY)*2];
        
        (* 混合公式：平滑加权 *)
        0.2 * (1 - s1) +           (* 远用区权重 *)
        (addPower/corridorLen * 1.8) * (s1 - s2 * 0.8) + (* 通道区权重 *)
        1.0 * s2                   (* 近用区权重 *)
    ];

    (* --- 核心改进 C: 平滑像散计算 --- *)
    astigFunction[x_, y_] := Module[{dist, raw},
        (* 距离清晰边界的距离 *)
        dist = Abs[x] - boundaryCurve[y];
        
        (* Ramp 替代 If: 小于0取0，大于0取值。 *)
        (* Power(..., 1.2) 让起坡更自然，不是生硬的直线 *)
        raw = stiffnessField[y] * Ramp[dist]^1.1;
        
        (* 限制最大值，防止色彩溢出 *)
        Min[raw, addPower * 1.2]
    ];

    (* --- 绘图：高精度渲染 --- *)
    plot = ContourPlot[
        astigFunction[x, y],
        {x, -xMax, xMax}, {y, yMin, yMax},
        
        (* 渲染引擎设置：消除锯齿的关键 *)
        PlotPoints -> 80,         (* 提高采样点密度 *)
        MaxRecursion -> 3,        (* 允许更细的网格细分 *)
        Exclusions -> None,       (* 禁止寻找断点，强制连续渲染 *)
        
        (* 视觉风格 *)
        Contours -> Range[0.25, 3.5, 0.25],
        ColorFunction -> "TemperatureMap",
        ColorFunctionScaling -> False, (* 锁定绝对度数颜色，便于对比 *)
        
        Frame -> True,
        FrameLabel -> {None, None},
        PlotLabel -> Style[designType, Bold, 13],
        
        (* 装饰覆盖层 *)
        Epilog -> {
            {Dashed, White, Opacity[0.5], Line[{{-20, startY}, {20, startY}}]},
            {Dashed, White, Opacity[0.5], Line[{{-20, endY}, {20, endY}}]},
            {Text[Style["配镜十字", White, Bold, 10], {0, 5}]},
            {Thick, White, Line[{{-1, 2}, {1, 2}}], Line[{{0, 1}, {0, 3}}]}
        },
        ImageSize -> 350
    ];
    
    plot
];

(* ========================================================= *)
(*   输出：高保真对比图 *)
(* ========================================================= *)

Print[Style["V3.0 高保真模拟：消除计算伪影", "Section", Blue]];

Grid[{
    {
        SimulateSmoothPAL[2.00, 14, "均衡型 (Balanced) \nADD +2.00"],
        SimulateSmoothPAL[3.00, 12, "短通道 (Short/Hard) \nADD +3.00"]
    }
}, Spacings -> {1, 1}]

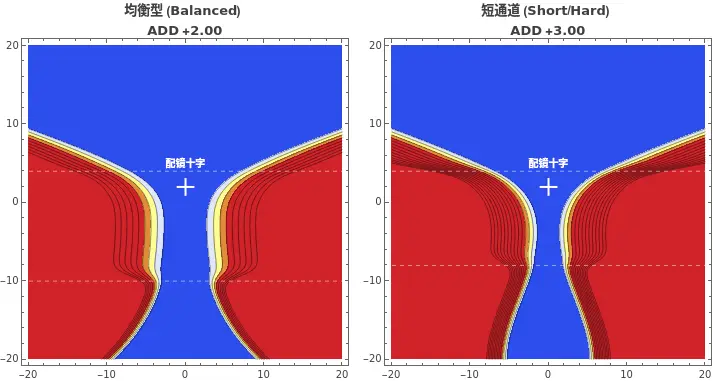
An image to describe post

运行结果解读

场景 A (短通道)：像散梯度高达 0.42 D/mm。这意味着患者瞳孔只需往旁边转 2mm，就会遇到近 1.00D 的散光。这就像透过钥匙孔看世界。
场景 B (长通道)：像散梯度降至 0.28 D/mm。视野明显变宽。
结论：对于高 Add 的患者，尽量劝说其选择大框、长通道。这不是审美问题，这是数学问题。

6.5 决策矩阵：硬性 vs 软性设计

既然像散无法消除（因为公式里那个 $2$ 无法变成 $0$ ），设计师唯一能做的就是搬运像散。这引出了两种截然不同的设计哲学，也就是你在订片单上看到的“硬性 (Hard)”和“软性 (Soft)”设计。

我们可以用 “水床效应” 来解释：像散的总量是一定的（像水床里的水），你按下这一头，那一头就会鼓起来。

6.5.1 临床决策对照表

Dr. X，作为架构师，你需要根据患者的职业和性格来选择“搬运”策略：

设计类型	几何策略 (水床效应)	优点	缺点	适用人群	沟通话术
硬性设计 (Hard)	把像散狠狠地推到最边缘，保住中间的大片净土。	远用和近用视野宽阔，中心极清晰。	像散区像悬崖一样陡峭。一旦转头快了，周围景物会“晃动”（游泳感）。	工程师、绘图员（静态注视为主，对直线变形敏感）。	“这副眼镜中间看东西特别清楚，直线特别直。但走路时请多转头，少转眼球，否则边缘会有点晕。”
软性设计 (Soft)	把像散均匀地“摊大饼”，允许少许散光渗入中心。	像散梯度平缓，从清晰到模糊过渡自然，动态视觉好，不容易晕。	绝对清晰的范围稍微变窄了。	初戴者、高尔夫球手、司机（动态视觉要求高，头动频繁）。	“这副眼镜戴着很舒服，走路不晕。虽然看极远处可能有一点点柔和感，但它能让你全天候适应各种活动。”

6.6 结语：从推销员到架构师

Dr. X，下次当患者要求“完美镜片”时，不要再用含糊的商业术语敷衍。

请拿出纸笔，画一个简单的图，告诉他：

“您的眼睛需要完成从远到近 2.50D 的跨越。为了实现这个跨越，我们必须在空间的某个维度支付‘过路费’。

我们可以选择支付‘视野宽度’（选短通道），也可以选择支付‘边缘清晰度’（选软性设计）。

没有不收费的道路，但我可以为您设计一条最划算的路线。”

这就是闵克维茨定理给你的底气。你不再是一个售卖镜片的推销员，你是一名在弯曲光场中权衡利弊的空间架构师。

在下一章，我们将离开镜片表面，深入角膜内部。我们将看到，那个被我们简化的“眼压”，实际上是一个更加复杂的 应力张量。

第7章：应力张量——不仅是眼压

“眼压是流体的独白，应力是组织的呐喊。当我们只倾听前者时，便错过了角膜最痛苦的求救信号。”

7.1 引言：数字的欺骗

Dr. X，你的诊室里肯定发生过这种“灵异事件”：

场景 A：一位老人的眼压只有 11 mmHg（绝对的安全区），但他的视神经却像融化的蜡烛一样逐年枯萎，视野缺损无情进展。（正常眼压性青光眼）
场景 B：一位年轻人的眼压高达 24 mmHg，被别的医生判了“青光眼死刑”，但你随访了五年，他的视神经纹丝不动，健康得令人发指。（高眼压症）
你可能会怀疑眼压计坏了，或者角膜厚度 (CCT) 在捣乱。你开始用各种公式去“修正”眼压值。
但作为 “空间的架构师”，我要告诉你一个残酷的真相：修正公式大多是安慰剂。
因为你试图用一个**标量（眼压，Pressure）去描述一个复杂的张量（应力，Stress）**现象。这就像试图用“体重”来衡量一个人的“武功高低”一样，虽然有关联，但完全是两个维度的概念。
本章的任务，就是给你一副 “力学透视镜”。我们将不再纠结于 GAT 读数的准确性，而是直接穿透角膜，去看看那些肉眼不可见的“力线”是如何撕裂组织的。

7.2 物理直觉：从“气球”到“果冻”

在讲数学之前，我们先做一个简单的思想实验。

7.2.1 眼压 vs. 应力：谁才是凶手？

想象你手里有一个气球（代表角膜）。

眼压 (Pressure)：是你吹进去的气。它是一个标量，只有大小，没有方向（或者说，它向四面八方均匀施压）。
应力 (Stress)：是气球橡胶壁感受到的拉扯感。它是一个张量，既有大小，又有方向。
关键点来了：
如果你在气球上贴一块胶布（局部变硬），虽然里面的气压没变，但这块胶布周围的应力会突然集中。
如果你把气球某处磨薄了，虽然气压没变，但薄弱处的应力会爆表，导致炸裂。
临床翻译：
青光眼损伤视神经的，不是眼压，是筛板 (Lamina Cribrosa) 承受的应力。
圆锥角膜扩张的，不是眼压，是基质层胶原纤维承受的应力。
既然凶手是“应力”，为什么我们只测“眼压”？
因为眼压好测（喷一下气就行），而应力看不见摸不着。但今天，我们要改变这一点。

7.2.2 为什么必须是“张量”？

想象一块方形的果冻。

正应力（拉伸/压缩）：你垂直往下按，果冻变矮了。
剪切应力（错位）：你把手掌放在果冻顶上，水平一推。果冻歪了。
角膜不只是受拉（眼压撑开），它还受剪切（揉眼、眨眼）。简单的眼压读数（标量）无法描述这种复杂的“歪”，只有 应力张量（一个 $3 \times 3$ 的矩阵） 才能完整描述果冻内部每一个点受力的状态。

7.3 核心定律：拉普拉斯的修正

Dr. X，你一定背过这个公式：

T = \frac{P \cdot R}{2t}

(壁张力 = 眼压 $\times$ 半径 $\div$ 2倍厚度)

这是经典的拉普拉斯定律。它告诉你：角膜越薄（ $t$ 小）、越陡（ $R$ 小），张力就越大。

但是，Cynthia Roberts 教授（眼生物力学大神）会告诉你：这个公式是给完美的球体用的，不是给角膜用的。

真实的角膜是 各向异性 (Anisotropic) 的。

顺纹拉：沿着胶原纤维的方向，它像钢丝一样硬。
逆纹拉：垂直于胶原纤维的方向，它像果冻一样软。
当我们做 LASIK 或 SMILE 手术切断了部分神经纤维时，我们实际上是破坏了角膜的“钢筋网”。这时候，单纯看剩余厚度 (Residual Bed Thickness) 是不够的，我们必须看剩余的力学强度。

7.4 计算眼科学实战：Wolfram 角膜应力云图

让我们用 Wolfram 语言写一段代码，不再看枯燥的数字，而是画出角膜上的 “刺猬图”（矢量场）。

这些箭头代表了应力的方向和大小。

(* --------------------------------------------------------- *)
(*   程序名称：Corneal Stress Tensor Visualizer (角膜应力张量显微镜) *)
(*   功能：模拟并可视化角膜表面的薄膜应力分布 (Laplace模型)       *)
(*   核心逻辑：应力(σ) ≈ (眼压 × 曲率半径) / (2 × 厚度)           *)
(* --------------------------------------------------------- *)

ClearAll[VisualizeCornealBiomechanics];

VisualizeCornealBiomechanics[pressure_, type_] := Module[
    {
        (* 1. 几何与物理模型参数 *)
        gridRange = 3,     (* 模拟角膜直径范围 mm *)
        corneaShape,       (* 高度函数 Z(x,y) *)
        thicknessMap,      (* 厚度函数 T(x,y) *)
        stressCalculator,  (* 应力计算函数 *)
        
        (* 辅助变量 *)
        normalVec, tangentVec, zVal, thickness, stressVal,
        arrowColor, arrowScale,
        surfacePlot, vectorField,
        
        (* 模型参数设定 *)
        coneCenter = {0.8, -0.5}, (* 圆锥偏心位置 *)
        coneHeight, coneWidth
    },

    (* ----------------------------------------------------- *)
    (* 2. 定义角膜形态 (正常 vs 圆锥) *)
    (* ----------------------------------------------------- *)
    Switch[type,
        "Normal", 
        (
            coneHeight = 0; 
            coneWidth = 1;
        ),
        "Keratoconus", 
        (
            coneHeight = 1.2; (* 圆锥突起高度 *)
            coneWidth = 0.8;  (* 圆锥底宽 *)
        )
    ];

    (* 基础形态：抛物面 *)
    (* 圆锥形态：基础 + 高斯突起 *)
    corneaShape[x_, y_] := (x^2 + y^2)/18 + 
        coneHeight * Exp[-((x - coneCenter[[1]])^2 + (y - coneCenter[[2]])^2) / coneWidth];

    (* ----------------------------------------------------- *)
    (* 3. 定义厚度分布 (关键病理特征) *)
    (* ----------------------------------------------------- *)
    (* 正常角膜：周边厚，中心稍薄 *)
    (* 圆锥角膜：病灶处急剧变薄 (应力恶化的核心原因) *)
    thicknessMap[x_, y_] := Module[{baseThick, coneThinning},
        baseThick = 0.55 + 0.02 * (x^2 + y^2); (* 正常分布: 550um *)
        
        (* 如果是圆锥，病灶处厚度减少 *)
        coneThinning = If[type == "Keratoconus",
            0.25 * Exp[-((x - coneCenter[[1]])^2 + (y - coneCenter[[2]])^2) / coneWidth],
            0
        ];
        
        baseThick - coneThinning
    ];

    (* ----------------------------------------------------- *)
    (* 4. 计算生物力学应力 (简化的 Laplace Law) *)
    (* ----------------------------------------------------- *)
    (* 应力与厚度成反比。越薄的地方，受到的撕扯力越大 *)
    stressCalculator[x_, y_] := pressure / (thicknessMap[x, y] * 100); 

    (* ----------------------------------------------------- *)
    (* 5. 生成矢量场 (刺猬的刺) *)
    (* ----------------------------------------------------- *)
    vectorField = Table[
        Module[{n, t1, t2, pos, s, col, len},
            pos = {x, y, corneaShape[x, y]};
            s = stressCalculator[x, y]; (* 获取局部应力值 *)
            
            (* 计算法线向量 *)
            n = Normalize[{-Derivative[1, 0][corneaShape][x, y], -Derivative[0, 1][corneaShape][x, y], 1}];
            
            (* 构造切向向量 (代表沿着角膜表面的拉力) *)
            (* 这里简化为沿径向的切线，这是扩张的主要方向 *)
            t1 = Normalize[{x, y, 0} - Dot[{x, y, 0}, n]*n];
            
            (* 视觉编码：应力越大，箭头越红、越长 *)
            col = ColorData["TemperatureMap"][Rescale[s, {0.2, 0.8}]]; 
            len = Rescale[s, {0.2, 0.8}, {0.2, 0.6}]; 
            
            (* 如果应力过大，加粗箭头 *)
            {
                col, 
                Arrowheads[0.015 + (s * 0.02)], 
                Opacity[0.8],
                Arrow[{pos, pos + t1 * len}] (* 绘制切向拉力箭头 *)
            }
        ],
        {x, -gridRange, gridRange, 0.4}, {y, -gridRange, gridRange, 0.4}
    ];

    (* ----------------------------------------------------- *)
    (* 6. 渲染 3D 场景 *)
    (* ----------------------------------------------------- *)
    surfacePlot = Plot3D[
        corneaShape[x, y],
        {x, -gridRange, gridRange}, {y, -gridRange, gridRange},
        
        (* 表面着色：显示应力云图 *)
        ColorFunction -> Function[{x, y, z}, ColorData["TemperatureMap"][Rescale[stressCalculator[x, y], {0.2, 0.8}]]],
        ColorFunctionScaling -> False,
        Mesh -> None,
        PlotStyle -> Opacity[0.3], (* 半透明，以便看到内部结构 *)
        Lighting -> "Neutral"
    ];

    (* 组合输出 *)
    Show[
        surfacePlot,
        Graphics3D[vectorField], (* 叠加矢量场 *)
        
        Boxed -> False,
        Axes -> False,
        ViewPoint -> {0, -2, 1.5}, (* 医生视角 *)
        ImageSize -> 350,
        PlotLabel -> Style[
            Switch[type,
                "Normal", "正常角膜 (Normal)\n受力均匀",
                "Keratoconus", "圆锥角膜 (Keratoconus)\n局部应力崩溃"
            ], 
            Bold, 14, RGBColor[0.2, 0.2, 0.2]
        ]
    ]
];

(* ========================================================= *)
(*   临床实战：对比眼压相同但结构不同的两只眼睛 *)
(* ========================================================= *)

Print[Style["--- 第7章：透过眼压看应力 ---", "Section", Blue]];
Print["设定眼压 (IOP): 15 mmHg (临床上完全正常的数值)"];
Print["请观察：虽然气压一样，但红色的箭头揭示了组织内部的‘撕裂感’。"];

Row[{
    VisualizeCornealBiomechanics[15, "Normal"],
    Spacer[20],
    VisualizeCornealBiomechanics[15, "Keratoconus"]
}]

An image to describe post

运行结果解读

当你运行这段代码，你会看到一个惊人的现象：

正常角膜：箭头分布均匀，长短一致，说明受力平衡。
圆锥角膜：在圆锥突起的基底部 (Base)，会出现一圈血红色的长箭头。
- 这不仅是几何上的陡峭，这是力学上的 应力集中 (Stress Concentration)。
- 洞察：这就像撕开包装袋一样，一旦有一个缺口（应力集中点），裂痕就会沿着那个点迅速扩大。圆锥角膜就是这样被“撕”开的。

7.5 决策矩阵：从“地毯式轰炸”到“精确制导”

既然我们看到了应力分布是不均匀的，那么现在的角膜交联术 (CXL) 是不是太粗糙了？

目前的 CXL 就像地毯式轰炸：对着角膜中央 9mm 均匀照射紫外线。

结合应力张量理论，未来的治疗将是矢量引导的 (Vector-Guided)：

治疗策略	传统 CXL (Dresden Protocol)	矢量引导 CXL (Vector-Guided)
理念	哪里有病治哪里（覆盖中央）。	哪里软弱加固哪里。
照射区域	圆形均一光斑。	根据 Wolfram 算出的“红色箭头”区域定制图案。
能量分布	均匀分布。	在应力集中环（圆锥基底）加强能量，封锁扩张路径。
比喻	给整条路重铺柏油。	给轮胎即将爆裂的最薄处打补丁。
Dr. X 的决策	适用于早期、形态规则的病例。	适用于偏心圆锥、极薄角膜的抢救性治疗。

7.6 结语：做“力”的捕手

Dr. X，这一章的内容可能有点烧脑，但请记住最核心的一句话：

眼压是幻象，应力才是真相。

下次当你面对一位“正常眼压”的青光眼患者，或者一位想要做手术的薄角膜患者时，请闭上眼睛，想象那块透明组织内部正在进行的拔河比赛。

不要只盯着 GAT 的读数。
去思考胶原纤维的走向。
去寻找那些看不见的“红色箭头”。
你不再是一个只会读数的眼压监测员。你是能够洞察力学平衡、预判组织崩塌的空间架构师。
在下一章，我们将进入更激动人心的领域——逆向工程。既然我们已经看透了角膜的形状和受力，我们能不能反过来，设计一个完美的镜片去“中和”这一切？闵可夫斯基问题将给你答案。