第一部分:内蕴之眼——曲面与诊断
第1章 地图不是疆域——地形图的谎言
“地图不等于疆域。” —— 阿尔弗雷德·科日布斯基 (Alfred Korzybski)
1.1 引言:Dr. X 的屏幕焦虑
让我们把镜头对准诊室里的 Dr. X。
他是一位经验丰富的眼科医生,裂隙灯用得炉火纯青,检眼镜下能一眼认出微小的视网膜裂孔。但最近,他感到一种莫名的焦虑。以前,他看的是病人的眼睛;现在,他大部分时间都在看屏幕。
无论是角膜地形图绚丽的彩色圆盘,还是 Optos 广角眼底图上那张绿色的视网膜全景,这些图像虽然清晰,却经常让他陷入困惑:
- “为什么同一只圆锥角膜,在这个模式下像个领结,换个按钮就变成了岛屿?”
- “为什么这张眼底照边缘的裂孔看起来大得吓人,但我进去做激光时发现它其实很小?”
Dr. X 的直觉是对的。这不仅仅是视觉误差,这是数学上的必然。
本章的任务,就是带你透过屏幕上那些漂亮的像素,看到背后的数学骨架。我们要揭示一个残酷的真相:你看到的每一张二维医学图像,本质上都是对三维眼球的“扭曲投影”。
如果不理解这种扭曲,我们就如同拿着一张错误的地图在航海,注定会在看似直线的航程中触礁。
1.2 维度的诅咒:撕裂的橘子皮

眼球是三维的,屏幕是二维的。这就是所有问题的根源。
在数学家眼中,眼球表面(无论是角膜还是视网膜)是一个流形 (Manifold) ——一个局部看起来像平面,但整体弯曲的空间。当仪器试图把这个弯曲的表面“画”在平坦的电脑屏幕上时,它必须面对一个物理铁律。
我们来做一个著名的思维实验:撕裂橘子皮。
试想你手里拿着半个橘子皮(代表视网膜)。你的任务是把它完全平整地压在桌面上,做成一张地图。你会发现只有两种结果:
- 撕裂:橘子皮裂开无数道口子(数据不连续)。
- 压烂:你强行把皮压平,原本靠在一起的纹理被拉伸变形(度量失真)。
眼科仪器选择了后者。为了把弯曲的角膜或视网膜“压”进平面的地形图里,算法必须对图像进行拉伸。这种拉伸并不是均匀的,它欺骗了你的眼睛。
在微分几何中,描述这种拉伸的工具叫度量张量 (Metric Tensor)。不用担心这个名词,你可以把它想象成“换算系数”。在屏幕中心,1毫米可能代表真实的1毫米;但在屏幕边缘,1毫米可能代表真实的5毫米。
如果我们忽略这个系数,直接用尺子在屏幕上量距离,那就是在自我欺骗。
1.3 地形图的罗生门:轴向图 vs. 切向图
在角膜屈光手术筛查中,最让 Dr. X 头疼的莫过于“轴向曲率”和“切向曲率”打架的问题。同一只眼睛,两张图给出的形态截然不同。
到底谁在撒谎?答案是:都在撒谎,只是撒谎的方式不同。
1.3.1 轴向曲率 (Axial/Sagittal):光学的“美颜相机”
原理:它假设光线都围绕一个中心轴旋转。它计算的是表面法线到光轴的距离。
谎言:为了维持“围绕中心”的假设,它会强行抹平局部的微小凹凸。
临床后果:它像开了十级美颜。早期的圆锥角膜突起,在轴向图上可能被磨皮成一个温和的散光。
什么时候看它:算度数时。 因为光线进入眼睛的方式确实接近这种假设,所以在计算人工晶体(IOL)度数时,它是准确的。
1.3.2 切向曲率 (Tangential/Instantaneous):形态的“显微镜”
原理:它不关心光轴,只关心角膜表面局部的弯曲程度(密切圆半径)。
谎言:它对噪点极其敏感。泪膜稍微不稳,图上就会出现一堆杂乱的斑点。
临床后果:它太诚实了,诚实到充满了噪点。
什么时候看它:看病时。 当你需要定位圆锥角膜的顶点,或者观察塑形镜(OK镜)的压痕位置时,必须看切向图。
Dr. X 的生存法则:
不要试图寻找一张“正确”的地图。
- 问光学问题(视力好不好?),看轴向图。
- 问形状问题(角膜有没有歪?),看切向图。
1.4 广角眼底的幻象:巨大的裂孔
现在我们转过身,看看眼球的后面。Optos 等超广角成像系统(UWF)彻底改变了眼底病诊疗,能一眼看到200度的范围。
但你注意到那个奇怪的现象了吗?位于图像边缘的视网膜裂孔,看起来总是巨大无比;而视盘看起来却很正常。
这是因为广角成像通常采用一种类似球极平面投影 (Stereographic Projection) 的算法。这种投影有一个著名的数学性质:保角性 (Conformality)。
- 保角(优点):它能完美保持局部的形状。圆形的血管截面在图上还是圆的,血管的分叉角度也是准的。所以图像看起来很自然。
- 失面积(缺点):作为代价,它必须疯狂地牺牲面积准确性。
几何陷阱:根据黎曼几何原理,离中心越远,面积被放大的倍数就越夸张。在图像的最边缘,病灶面积可能被放大了数倍。
临床警示:
如果你在广角图边缘看到一个“巨大”的裂孔,千万别急着感叹。实际上,它可能只是一个小裂隙。如果你按照图上的大小去打激光,你可能会烧灼过大范围的健康视网膜。
永远记住:在广角影像的边缘,不要相信你的直觉,不要相信面积。
1.5 计算眼科学的介入:找回真实的距离
既然屏幕全是谎言,我们该怎么办?
这时候,我们需要请出计算眼科学。我们不再依赖肉眼估算,而是利用 Wolfram Language 这样的工具,重新计算被投影丢失的真实信息。
还记得那个“撕裂橘子皮”的比喻吗?既然我们已经把橘子皮压扁了,数学家可以反向操作,通过度量张量把扁平的图像“还原”回三维曲面,然后计算真实的距离。
下面是一个简单的概念演示。这段代码不是为了让你成为程序员,而是为了展示:我们可以把模糊的图像猜测,转化为精确的数学事实。
(*
Wolfram 概念代码:从“地图距离”还原为“真实距离” (修复版)
Dr. X 遇到的问题:
直接用尺子量屏幕(EuclideanDistance)是错的。
直接问 RegionDistance 也是错的(那是问点到面的垂直距离)。
正确方法:
我们需要定义一条在 x-y 平面上看似直线的路径,
将其“投影”回弯曲的角膜表面,然后用积分计算这条 3D 曲线的真实长度。
*)
ClearAll[corneaZ, ComputeGeoDistance, p1, p2, mapDistance, realDistance];
(* 1. 定义角膜的数学模型 *)
(* 这是一个旋转对称的非球面模型。R = 7.8mm 是基弧半径 *)
corneaZ[x_, y_] := 8.0 - (x^2 + y^2) / (2 * 7.8);
(* 2. 定义“测地线距离”计算引擎 *)
ComputeGeoDistance[pt1_List, pt2_List] := Module[
{pathParam, x1, y1, x2, y2, curve3D},
(* 提取坐标 *)
{x1, y1} = pt1[[1 ;; 2]];
{x2, y2} = pt2[[1 ;; 2]];
(*
核心逻辑:
我们在“地图”(x-y平面)上画一条线,参数 t 从 0 到 1。
然后把这条线“贴”到角膜曲面函数 z(x,y) 上。
*)
pathParam[t_] := {
x1 + (x2 - x1) * t, (* x 随 t 线性变化 *)
y1 + (y2 - y1) * t, (* y 随 t 线性变化 *)
corneaZ[ (* z 随 x,y 变化,体现曲率 *)
x1 + (x2 - x1) * t,
y1 + (y2 - y1) * t
]
};
(*
使用 ArcLength 进行积分计算。
这相当于拿着一把无限精细的软尺,沿着起伏的表面测量。
*)
Return[ArcLength[pathParam[t], {t, 0, 1}]]
];
(* --- 模拟临床场景 --- *)
(* 场景:角膜地形图上的两个点,位于同一子午线上 *)
(* 瞳孔上方 1mm 处 *)
p1 = {0, 1, corneaZ[0, 1]};
(* 瞳孔上方 4mm 处 *)
p2 = {0, 4, corneaZ[0, 4]};
(* --- 执行计算 --- *)
(* A. 医生的直觉:看图估算 (二维欧氏距离) *)
mapDistance = EuclideanDistance[{p1[[1]], p1[[2]]}, {p2[[1]], p2[[2]]}];
(* B. 算法的真相:空间计算 (三维黎曼距离/弧长) *)
realDistance = ComputeGeoDistance[p1, p2];
(* --- 输出报告 --- *)
Print[Style["------------------------------------------------", Color -> Gray]];
Print[Style["计算眼科学报告:距离校正", FontWeight -> "Bold", FontSize -> 16]];
Print[""];
Print["测量对象: 角膜上方垂直子午线 1mm 至 4mm 处"];
Print[""];
Print["1. 地形图平面距离 (Map Distance): ",
Style[ToString[NumberForm[mapDistance, {3, 3}]] <> " mm", Red]];
Print[" (这是我们在屏幕上看到的,被压扁了)"];
Print[""];
Print["2. 角膜真实弧长 (True Arc Length): ",
Style[ToString[NumberForm[realDistance, {3, 3}]] <> " mm", Blue, FontWeight -> "Bold"]];
Print[" (这是光线或隐形眼镜真正覆盖的距离)"];
Print[""];
(* 计算误差百分比 *)
errorPercent = (realDistance - mapDistance)/mapDistance * 100;
Print[">>> 丢失的信息量 (误差): ", NumberForm[errorPercent, {3, 2}], "%"];
Print[Style["------------------------------------------------", Color -> Gray]];
(* 可视化:展示为什么距离变长了 *)
Show[
Plot3D[corneaZ[x, y], {x, -1, 1}, {y, 0, 5},
PlotStyle -> Opacity[0.3, Blue], Mesh -> None, Boxed -> False, Axes -> False,
PlotLabel -> "角膜侧面观:红色直线 vs 蓝色曲线"],
(* 真实的弯曲路径 *)
ParametricPlot3D[{0, 1 + 3 t, corneaZ[0, 1 + 3 t]}, {t, 0, 1},
PlotStyle -> {Blue, Thickness[0.02]}],
(* 被误解的直线距离 *)
Graphics3D[{Red, Dashed, Thickness[0.01], Line[{p1, p2}]}],
ImageSize -> Medium, ViewPoint -> {2, -2, 1}
]

1.6 小结:从看图到看空间
第一章的旅程结束了。我们没有解决所有问题,但我们不仅看到了现象,还看到了本质。
- 我们明白了 “地图不是疆域” :所有的地形图和眼底照都在通过某种方式“撒谎”,以换取二维的展示。
- 我们学会了警惕 轴向图的平滑谎言 和 切向图的噪点真相 。
- 我们知道了 广角影像边缘的面积 是不可信的。
对于 Dr. X 来说,这不仅仅是知识的增加,更是认知的觉醒。你不再是被动的“看图者”,你开始意识到你正在处理的是一个弯曲的空间。
但是,还有一个终极问题悬而未决:
既然地形图这么不可靠,既然隐形眼镜引起的翘曲 (Warpage) 和病理性的圆锥角膜 (Keratoconus) 在图上看起来都像红色的“陡峭”,我们到底该怎么区分它们?有没有一种几何属性,是无论怎么投影、怎么弯曲都 绝对不变 的?
有的。那个属性叫做 高斯曲率 。那是一把数学赐予的“测谎仪”。在下一章,我们将揭开它的面纱。
第2章:绝妙定理与圆锥角膜测谎仪
“如果一个曲面在不被撕裂或拉伸的情况下发生弯曲,它的高斯曲率保持不变。”
—— 卡尔·弗里德里希·高斯 (Carl Friedrich Gauss), 1827
2.1 引言:红色的假象
(Introduction: The Red Mirage)
让我们回到 Dr. X 的诊室。今天是个忙碌的上午,坐在裂隙灯前的是一位年轻的近视患者,戴了十年的软性隐形眼镜。
Dr. X 习惯性地打开 Pentacam 地形图,眉头立刻皱了起来。在 轴向曲率图 (Axial Map) 上,角膜下方出现了一片刺眼的红色区域,呈现出典型的不对称“领结”状 (Asymmetric Bowtie)。
警报在他脑海中拉响:“下方陡峭?这是圆锥角膜 (Keratoconus) 的铁证!”
但真的是这样吗?Dr. X 陷入了犹豫。裂隙灯下看不到 Vogt 纹,也没有 Fleischer 环。这到底是一个需要立即做角膜交联术 (CXL) 的早期圆锥,还是仅仅因为隐形眼镜戴久了,把角膜“压”出了一个坑 (Contact Lens Warpage)?
如果诊断为圆锥,患者将失去做近视手术的机会;如果误判为压痕而做了切削,则可能导致灾难性的医源性扩张。
在传统的临床路径中,Dr. X 唯一的办法是:“停戴隐形眼镜两周,再来复查。”这不仅效率低下,还充满了不确定性。
其实,Dr. X 不需要等待两周。如果他手里有一把测量“内蕴几何”的尺子,他只需要两秒钟就能看穿这个红色的假象。
本章就要交给你这把尺子——高斯绝妙定理 (Theorema Egregium)。
2.2 为什么地形图会撒谎?
(Why Topography Lies?)
为什么轴向图 (Axial) 和切向图 (Tangential) 在这个问题上失效了?
因为它们测量的都是 “外在形状” 。
想象你拿一张 A4 纸,把它卷成一个圆筒。
- 对于这一张纸(外在视角): 它的形状变了,从平面变成了曲面。轴向图会告诉你:“这里变陡了,曲率变大了。”
- 对于纸上的蚂蚁(内蕴视角): 蚂蚁爬过这张纸时,不会感觉到任何变化。三角形的内角和还是180度,两点间的距离也没有变。纸的本质没有变,它只是被弯曲了,没有被拉伸。

隐形眼镜导致的翘曲 (Warpage),就像是卷起来的纸。 角膜被物理力量压弯了,但角膜基质的纤维没有断裂,组织没有发生本质的拉伸。
然而,传统的地形图仪就像是从外部观察的人,它看到角膜“弯”了,就误以为它“病”了。为了识破这个谎言,我们需要像那只蚂蚁一样,从角膜的“内部”去测量它。
2.3 披萨定理:高斯的美味直觉
(The Pizza Theorem: Gauss’s Delicious Intuition)
如何从内部测量一个物体是否被“拉伸”了?我们不需要复杂的微积分,只需要一块披萨。
这就是著名的披萨定理,它是高斯绝妙定理在生活中的直接体现。
场景重现
当你在食堂拿起一片刚出炉的薄底披萨时,如果你平平地捏着边缘,披萨的尖端会因为重力而垂下去,馅料撒一地。
为了防止这种情况,你会本能地把披萨边缘折叠成一个“U”字形。奇迹发生了:披萨瞬间变硬了,尖端直挺挺地伸了出去。
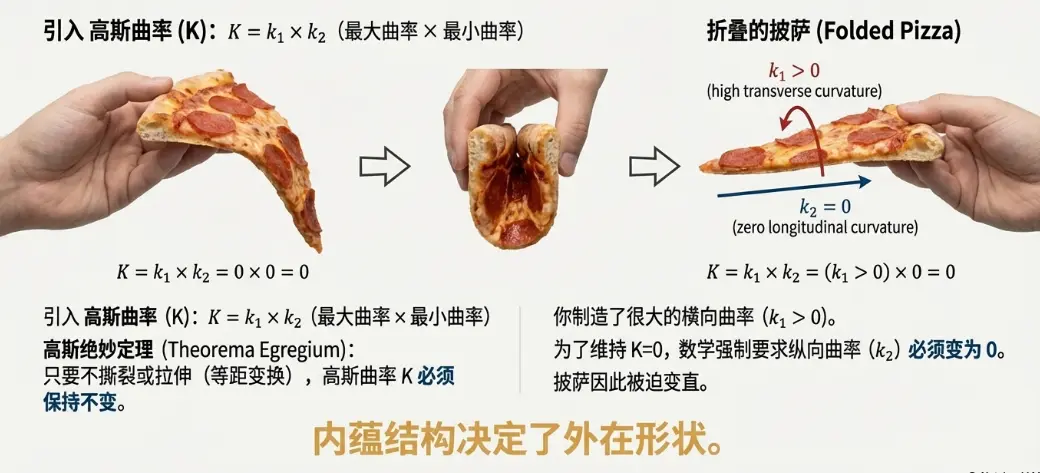
这里的几何魔法是什么?
高斯定义了一个核心指标:高斯曲率 ()。
其中 是最大弯曲方向的曲率, 是最小弯曲方向的曲率。
- 平放的披萨:它是平的,两个方向曲率都是0,所以 。
- 折叠的披萨:当你把边缘折成“U”形时,横向曲率 () 变得很大。但是,高斯绝妙定理告诉我们:只要披萨面饼没有被撕裂或拉伸(等距变换),它的高斯曲率 必须保持不变,依然为 0。
- 结局:既然 必须为 0,而 已经不为 0 了,那么数学强制要求纵向曲率 必须严格等于 0。也就是说,披萨在纵向上被迫变直了。
这就是内蕴几何的威力:结构决定了形状。
2.4 圆锥角膜测谎仪:红峰与蓝谷
(The Lie Detector: Red Peaks and Blue Valleys)
现在,我们将“披萨原理”应用到角膜诊断上。我们将所有角膜异常分为两类:
第一类:披萨模式 (Warpage / 翘曲)
- 物理过程:隐形眼镜压迫角膜。
- 几何本质:等距变换 (Isometric Deformation)。就像卷纸或折叠披萨。
- 高斯曲率 ():保持不变(绿色)。
- 诊断:无论轴向图上看起来多么红、多么陡峭,只要高斯曲率图是平坦的(接近0),这就是假性的。不需要手术,停戴镜片即可恢复。
第二类:气球模式 (Keratoconus / 圆锥角膜)
- 物理过程:角膜基质层胶原纤维断裂、变薄、凸起。
- 几何本质:非等距变换 (Non-isometric Deformation)。就像吹起的气球,或者怀孕时的腹部皮肤,表面积发生了局部的拉伸。
- 高斯曲率 ():剧烈变化。
- 诊断:圆锥顶点的 值会飙升(正曲率,红色),而为了代偿这种突起,周围往往会出现负曲率区域(马鞍面,蓝色)。
- 特征签名:“红峰蓝谷”。如果你在图上看到这种红蓝相间的拓扑结构,那就是真性病变。
Dr. X 的决策树:
- 轴向图红 + 高斯图绿 = 假警报 (Warpage)
- 轴向图红 + 高斯图红 = 真圆锥 (KC)
2.5 辅助证据:上皮层的填补游戏
为了双重保险,我们还可以引入第二个维度:角膜上皮 (Epithelium)。
上皮层就像是角膜上的“积雪”,它会自动填平地表的沟壑。
- 翘曲 (Warpage):角膜被压了一个坑。积雪(上皮)会把坑填满。所以,在变陡的地方,上皮层是增厚的。
- 圆锥 (KC):角膜自己从里面鼓出来了。为了维持表面光滑,积雪(上皮)在山顶会被刮薄。所以,在变陡的地方,上皮层是变薄的(以此形成著名的“甜甜圈征”)。
2.6 计算眼科学实战:Wolfram 测谎代码
(Computational Ophthalmology in Action)
道理讲通了,我们要把这个理论变成 Dr. X 手中的工具。我们不需要手动去算曲率,Wolfram Language 可以帮我们完成这一“降维打击”。
下面的代码展示了如何计算角膜网格的离散高斯曲率。核心算法使用了角度亏损 (Angle Deficit) ——这其实就是计算“披萨平铺时缺了多少角”。
(* 2.6 计算眼科学实战:Wolfram 测谎代码 (最终修复版) *)
ClearAll[ComputeDiscreteGaussianCurvature, AnalyzeCornealIntrinsicDeformation, SimulateCornea];
(* --------------------------------------------------------- *)
(* 🔧 核心引擎:角度亏损算法 (已修复索引提取) *)
(* --------------------------------------------------------- *)
ComputeDiscreteGaussianCurvature[mesh_] := Module[
{coords, polygons, cells, nVerts, angleSums, i, j, k, u, v, w, angA, angB, angC, K},
(* 1. 获取几何数据 *)
coords = MeshCoordinates[mesh];
nVerts = Length[coords];
(* [FIX HERE] 修复数据结构提取错误 *)
(* MeshCells 返回 {Polygon[{1,2,3}], ...} *)
(* 我们使用 Case 或 First 提取其中的索引列表 *)
polygons = MeshCells[mesh, 2];
cells = First /@ polygons; (* 提取 Polygon 内部的 {i,j,k} *)
(* 初始化 *)
angleSums = ConstantArray[0.0, nVerts];
(* 2. 遍历计算 (如果是几万个面的大模型,这里可以用 Compile 加速,但在演示中 Do 足够了) *)
Do[
{i, j, k} = cell;
{u, v, w} = coords[[{i, j, k}]];
(* 向量角计算 *)
angA = VectorAngle[v - u, w - u];
angB = VectorAngle[u - v, w - v];
angC = VectorAngle[u - w, v - w];
(* 累加到对应的顶点 *)
angleSums[[i]] += angA;
angleSums[[j]] += angB;
angleSums[[k]] += angC;
, {cell, cells}];
(* 3. 计算高斯曲率 K = 2Pi - Sum(Angles) *)
K = 2 Pi - angleSums;
(* 4. 边界清洗:移除边界上的非流形伪影 *)
(* 简单的启发式过滤:如果曲率绝对值大于 1.0 (约57度缺角),通常是边界噪音 *)
K = If[Abs[#] > 1.0, 0.0, #] & /@ K;
Return[K];
];
(* --------------------------------------------------------- *)
(* 🏥 临床工具:可视化模块 (增强对比度) *)
(* --------------------------------------------------------- *)
AnalyzeCornealIntrinsicDeformation[mesh_] := Module[
{vertexCurvatures, maxK, diagnosis, vertexColors, legend},
vertexCurvatures = ComputeDiscreteGaussianCurvature[mesh];
maxK = Max[vertexCurvatures];
(* 诊断逻辑 *)
diagnosis = Which[
maxK < 0.08,
Style["✅ 诊断建议:角膜翘曲 (Warpage)\n 理由:内蕴曲率平缓。", Darker[Green], Bold, 15],
maxK >= 0.08,
Style["🚨 警报:疑似圆锥角膜 (Keratoconus)\n 理由:检测到高斯曲率峰值 (K > 0.08)!这是拓扑结构异常。", Red, Bold, 15]
];
Print[diagnosis];
Print["峰值高斯曲率 (Max K): ", NumberForm[maxK, {4, 3}]];
(* [关键修改] 颜色映射范围调整 *)
(* 将 Rescale 的上限设为 0.15,这样任何突起都会变成鲜艳的红色 *)
vertexColors = ColorData["TemperatureMap"] /@ Rescale[vertexCurvatures, {0, 0.15}];
Graphics3D[{
EdgeForm[],
(* 使用高光材质让凸起更明显 *)
MaterialShading["Plastic", "SpecularColor" -> White, "Roughness" -> 0.2],
GraphicsComplex[MeshCoordinates[mesh], MeshCells[mesh, 2], VertexColors -> vertexColors]
},
Boxed -> False,
Lighting -> "Accent",
ImageSize -> Medium,
ViewPoint -> {0, -2, 2}, (* 调整视角侧看,更容易看到凸起 *)
PlotLabel -> Style["内蕴高斯曲率图 (The Lie Detector)", 16, Gray, Bold]]
]
(* --------------------------------------------------------- *)
(* 🧪 模拟造物:确保网格质量 *)
(* --------------------------------------------------------- *)
SimulateCornea[] := Module[{plot, mesh},
(* 使用 Plot3D 生成平滑曲面 *)
plot = Plot3D[
Sqrt[8.0^2 - x^2 - y^2] + 1.5 * Exp[-((x - 2)^2 + (y - 2)^2)/0.8], (* 收窄高斯包,让它更尖锐 *)
{x, -5, 5}, {y, -5, 5},
RegionFunction -> Function[{x, y, z}, x^2 + y^2 <= 25],
PlotPoints -> 80, (* 增加采样点以获得更细腻的网格 *)
Mesh -> None, Boxed -> False, Axes -> False
];
(* 转换为三角网格 *)
mesh = DiscretizeGraphics[plot];
Return[mesh];
];
(* ========================================================= *)
(* ▶️ 再次运行测试 *)
(* ========================================================= *)
Print["正在构建高精度角膜模型..."];
patientMesh = SimulateCornea[];
Print["模型构建完成。正在计算曲率..."];
AnalyzeCornealIntrinsicDeformation[patientMesh]

代码解读:
Dr. X,当你运行这段代码时,屏幕上会出现一个三维角膜模型。
- 不要看形状:哪怕模型看起来歪歪扭扭。
- 只看颜色:
- 如果是均匀的绿色/浅黄色:放心,那是“折叠的披萨”。哪怕轴向图红得发紫,这只角膜也是安全的。
- 如果出现了鲜红色的孤岛:那就是“吹起的气球”。不管视力多好,请立即干预。
2.7 结语:从光线的操作者到空间的架构师
(Conclusion: From Operator of Light to Architect of Space)
本章我们通过一片披萨,学到了微分几何中最深刻的定理之一:绝妙定理。
它告诉我们,表象(地形图的颜色)是可以伪造的,但本质(内蕴的度量)是无法撒谎的。
Dr. X,当你下次面对那张让人焦虑的红色地形图时,请不要只做一个“光线的操作者”,去纠结屈光度是高了还是低了。试着做一个“空间的架构师”,问自己一个问题:
“这只角膜是在弯腰(翘曲),还是骨折了(扩张)?”
掌握了高斯曲率,你就不再需要两周的等待。你拥有了看穿几何迷雾的透视眼。
在下一章,我们将离开角膜,沿着光路向后,去探索视网膜上的另一个几何谜题——为什么高度近视患者的 OCT 报告总是一片红?那里的地图,又发生了怎样的撕裂?
