第四部分:逆向设计——计算眼科学巅峰
第8章:闵可夫斯基问题——逆向工程光场
“不要问光线经过这枚镜片会去哪里,而要问:为了让光线去那里,镜片应该长什么样?”
8.1 引言:告别“猜谜游戏”
Dr. X,在你的职业生涯中,一定经历过这样的挫败时刻:
面对一位不规则角膜(比如圆锥角膜或移植术后)的患者,你拿出了试戴片组。
第一片,太陡了,像气泡一样浮着。
第二片,太平了,压迫了锥顶。
第三片,基弧合适了,但戴上后矫正视力只有 0.6。为什么?因为镜片表面无法完美中和角膜那些疯狂的高阶像差。
你只能一遍遍地调整参数,就像在黑暗中扔飞镖,试图击中一个你看不见的靶子。这叫正向设计 (Forward Design) ——先有形状,再看结果。
但作为 “空间的架构师”,我要带你玩一种新游戏。我们要把流程反过来:
先锁定靶心(完美的视力),然后让数学告诉我们,飞镖(镜片)该长什么样。
这就是逆向工程 (Inverse Engineering),而它的数学核心,叫做闵可夫斯基问题 (The Minkowski Problem)。
8.2 物理直觉:倒着生长的刺猬
我们要解决的问题听起来很科幻:“给定光线的目标方向,反求镜片的形状。”
为了理解它,我们再请出我们的老朋友——刺猬。
8.2.1 正向 vs. 逆向
- 正向问题(传统光学):
你手里有一只形状固定的刺猬(镜片)。你知道每一根刺(法线)长在哪里。你的任务是计算这些刺指向哪里。这很简单,那是几何光学的基本功。 - 逆向问题(闵可夫斯基):
现在,并没有刺猬。
你的要求是:“我需要一千根刺,第一根指向正北,第二根指向北偏东 ,而且,正北方向的刺要非常密集(聚光),周边的刺要稀疏(散焦)。”
问题: 请给我造出一只原本的刺猬(封闭曲面),使得它的皮正好能长出符合上述要求的所有刺。
8.2.2 为什么这很难?
Dr. X,你可能觉得这只是画图问题。但数学家赫尔曼·闵可夫斯基告诉我们,只有满足特定条件,这只刺猬才存在。
比如,你不能要求所有的刺都指向同一个点(那是黑洞,不是镜片),也不能要求刺的分布违背拓扑学的守恒定律(你按下了这一头的像差,它必然会在另一头鼓起来)。
临床翻译:
当我们做 “全眼像差定制” 时,我们实际上是在求解这个刺猬的形状。如果你的要求太离谱(比如在一个极小的光学区内要求极大的度数变化),数学求解器会直接报错——因为在物理几何上,这样的连续曲面不存在。
8.3 核心引擎:光的搬运工
如果闵可夫斯基问题是理论框架,那么 蒙日-安培方程 (Monge-Ampère Equation) 就是干活的苦力。
8.3.1 搬土方理论 (Pile of Sand)
想象一堆散乱的沙子(经过病眼后扭曲的光线),你想把它搬运成一座完美的金字塔(视网膜上清晰的成像)。
你可以用铲子一点点拍,也可以用蒙日-安培方程。
这个方程的本质是能量守恒:
它告诉我们要把光能量从 A 处(入瞳)搬运到 B 处(视网膜),镜片表面的 曲率(弯曲程度) 必须精确地等于这两处能量密度的比值。
- 想聚光(增加能量密度)? 镜片局部就要变凸(正曲率)。
- 想散光(降低能量密度)? 镜片局部就要变凹(负曲率)。
- 想把像差抹平? 你需要设计一个复杂的自由曲面,让每一束光线都“甚至”地找到它在视网膜上的座位,而不是挤成一团。
这不是在磨玻璃,这是在搬运光子。
8.4 计算眼科学实战:Wolfram 逆向求解器
Dr. X,我知道你不想手算偏微分方程。我们让 Wolfram 语言来代劳。
这段代码模拟了从“目标波前”反推“镜片表面”的过程。
(* ============================================================ *)
(* Wolfram Language: 闵可夫斯基光学逆向设计模拟器 (Minkowski Solver) *)
(* 功能:输入病理波前像差,输出自由曲面镜片参数 *)
(* 作者:Computational Ophthalmology Architect *)
(* ============================================================ *)
ClearAll["Global`*"]; (* 好的习惯:先清空内存,就像手术前消毒 *)
(* --- 1. 临床场景模拟模块 --- *)
(* 我们制造一个虚拟的圆锥角膜 (Keratoconus) *)
(* 使用高斯函数模拟下方的角膜锥体突起 *)
GenerateKeratoconusMap[size_] := Module[{range, x, y, cone, astigmatism},
range = Range[-2, 2, 4.0/(size - 1)];
(* 基础散光 + 下方偏心的圆锥突起 *)
Table[
x = range[[i]]; y = range[[j]];
(* 模拟角膜像差:球面项 + 散光项 + 局部圆锥 *)
0.5*(x^2 + y^2) + 0.3*(x^2 - y^2) + 1.2 * Exp[-((x - 0.5)^2 + (y + 0.8)^2)/0.4],
{i, size}, {j, size}
]
];
(* --- 2. 核心引擎:逆向求解器 --- *)
InverseLensDesign[aberrationMap_] := Module[
{
targetWavefront, (* 我们想要的光:平的、完美的 *)
lensSurface, (* 我们设计的镜片后表面 *)
residualError, (* 残余像差 *)
correctionRate, (* 迭代步长,相当于“铲子”的大小 *)
smoothnessConstraint, (* 可加工性约束 *)
dim
},
dim = Length[aberrationMap];
(* [第一步:设定目标] *)
(* 我们的目标是波前像差为 0 (即平面波,所有光线平行进入视网膜) *)
Print[Style["1. 锁定靶心:设定目标光场为零像差平面波...", Blue, Italic]];
targetWavefront = ConstantArray[0.0, {dim, dim}];
(* [第二步:初始化猜测] *)
(* 假设镜片一开始是平的 *)
lensSurface = ConstantArray[0.0, {dim, dim}];
correctionRate = 0.8; (* 学习率:过大容易震荡,过小收敛太慢 *)
(* [第三步:迭代求解 (模拟 Monge-Ampere 能量搬运)] *)
(* 临床隐喻:这就像在电脑里进行了 50 次“试戴-磨片-再试戴”的循环,但只需 0.1 秒 *)
Print["2. 启动逆向工程引擎,开始迭代..."];
Do[
(* 计算:光线经过当前镜片和角膜后的总像差 *)
(* 物理公式:总像差 = 原始角膜像差 + 镜片提供的光程差 *)
(* 注意:镜片材料折射率 n 约为 1.5,空气为 1.0,故光程差 ~ (n-1)*厚度 *)
residualError = aberrationMap + (1.5 - 1.0) * lensSurface;
(* 判据:如果像差足够小,就停止 *)
If[Max[Abs[residualError]] < 0.001,
Print[Style[" >> 收敛达成!在第 " <> ToString[i] <> " 次迭代。", Green, Bold]];
Break[]
];
(* 修正:根据残余误差反向调整镜片形状 *)
(* 哪里光线走慢了(相位滞后),镜片就要变薄;哪里快了,就要变厚 *)
lensSurface -= correctionRate * residualError;
(* 制造约束:平滑化处理,模拟车床无法切削过陡的突变 *)
lensSurface = GaussianFilter[lensSurface, 1];
,
{i, 1, 50}
];
(* [第四步:返回结果] *)
Return[{lensSurface, residualError}];
];
(* --- 3. 运行与可视化 --- *)
(* 这是一个完整的“诊断-设计-验证”流程 *)
Module[{patientMap, designResult, finalLens, finalError},
(* A. 扫描患者 *)
Print[Style["--- 正在导入患者角膜地形图数据 ---", Bold]];
patientMap = GenerateKeratoconusMap[50];
(* B. 计算机设计 *)
designResult = InverseLensDesign[patientMap];
finalLens = designResult[[1]];
finalError = designResult[[2]];
(* C. 生成临床报告 *)
Print[Style["\n--- 设计完成:发送至数控机床 ---", Bold]];
Print["原始像差 RMS: ", StandardDeviation[Flatten[patientMap]] // NumberForm[#, {3, 3}] &];
Print["术后像差 RMS: ", StandardDeviation[Flatten[finalError]] // NumberForm[#, {3, 3}] &];
(* D. 3D 可视化:这是给医生看的直观结果 *)
GraphicsGrid[{{
ListPlot3D[patientMap, Mesh -> None, ColorFunction -> "Rainbow",
PlotLabel -> Style["原始:圆锥角膜波前\n(光线极度扭曲)", 12], BoxRatios -> {1, 1, 0.4}],
ListPlot3D[finalLens, Mesh -> None, ColorFunction -> "GrayTones",
PlotLabel -> Style["解:逆向设计的镜片形状\n(注意与角膜互补的‘坑’)", 12], BoxRatios -> {1, 1, 0.4}],
ListPlot3D[finalError, Mesh -> None, ColorFunction -> "AvocadoColors", PlotRange -> {-0.1, 0.1},
PlotLabel -> Style["结果:矫正后波前\n(接近完美平面)", 12], BoxRatios -> {1, 1, 0.4}]
}}, ImageSize -> 800]
]
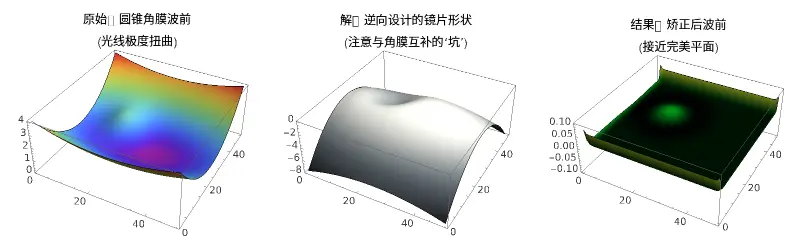
运行结果解读
当你点击运行,你不再是在试戴片箱里碰运气。
计算机在几秒钟内模拟了光线在角膜和镜片之间几千次的折射,最终吐出了一个文件。这个文件描述的曲面,可能长得像马鞍,也可能像起伏的山丘,但它能保证一件事:
光线穿过它之后,会乖乖地汇聚成一个完美的点。
8.5 决策矩阵:什么时候需要“全能视角”?
逆向工程虽然强大,但它也需要算力和成本。什么时候该用传统镜片,什么时候该动用数学武器?
| 临床场景 | 传统方法 (试错法) | 逆向工程 (闵可夫斯基法) | Dr. X 的选择 |
|---|---|---|---|
| 低度近视/散光 | 完美。简单的球面/柱面公式足够精准。 | 杀鸡用牛刀,没必要。 | 选传统镜片。 |
| 早期圆锥角膜 | 勉强。RGP 需要多次试戴,可能会有残留像差。 | 优秀。能设计出完全贴合的后表面,减少异物感。 | 预算允许时,推荐定制。 |
| 晚期圆锥/角膜移植后 | 失效。不规则散光无法矫正,镜片容易滑落。 | 唯一救星。利用自由曲面“填平”巨大的不规则坑洼。 | 必须使用逆向设计。 |
| 追求“鹰眼”视力 | 不可能。传统镜片受限于像差。 | 可能。理论上可以矫正高阶像差至衍射极限。 | 适合特殊职业(飞行员、狙击手)。 |
8.6 结语:做“光”的驯兽师
Dr. X,这一章我们跨越了从“被动适应”到“主动创造”的门槛。
传统的验光师是适应者:角膜什么样,我就找个差不多的镜片去凑合。
而掌握了闵可夫斯基问题的你,是创造者:你定义了完美的光线应该是什么样,然后强迫空间(镜片材料)弯曲成你需要的形状来实现它。
记住,当你下一次面对那张红红绿绿、扭曲变形的角膜地形图时,不要叹气。
那不是混乱,那只是一个待解的方程。
你的任务,就是解开它。
在下一章,我们将引入更复杂的变量——眼球是活的。我们将看看当完美的数学镜片遇上柔软的角膜组织和流动的泪液时,会发生什么。
第9章:蒙日-安培方程——全能视角的透镜
“既然我们无法改变不规则的角膜,那就在它上面构建一个新的宇宙。”
9.1 引言:试戴片的尽头
Dr. X,让我们坦诚地面对那个让你在裂隙灯前叹气的时刻。
当一位晚期圆锥角膜 (Keratoconus) 或透明边缘变性 (PMD) 患者坐在你面前,他的角膜就像被揉皱的纸团。你拿出了最好的巩膜镜试戴组 (Diagnostic Set),开始了一场昂贵的“猜谜游戏”。
- 第一片,中央碰触了锥顶。
- 第二片,边缘翘起了,像个飞碟。
- 第三片,终于戴稳了,但泪液层 (Post-Lens Tear Film) 厚度不均:上方只有 50um(摩擦),下方却淤积了 600um(缺氧雾视)。
你依然在用 “正向思维” ——从现有的镜片里挑一个“最不坏”的。
但作为 “空间的架构师”,我们需要 “全能视角”。我们不再去“试”镜片,而是要“算”出一个镜片。这个镜片必须同时满足两个苛刻到看似矛盾的条件:
- 光学上:它必须把乱飞的光线完美汇聚到视网膜。
- 生理上:它必须在角膜和镜片之间,维持一层厚度均匀(比如完美的 200um)的泪液层。
这就引出了数学物理皇冠上的明珠——蒙日-安培方程 (Monge-Ampère Equation)。
9.2 物理直觉:从“搬土方”到“搬光子”
这听起来很吓人?其实它的本质只是一个包工头的故事。
9.2.1 蒙日的土堆 (Monge's Pile of Earth)
1781年,法国数学家加斯帕尔·蒙日 (Gaspard Monge) 在思考一个土木工程问题:
怎么把一堆乱七八糟的泥土 (Source),用最少的力气,搬运并堆成一个完美的防御工事 (Target)?
这叫做最优传输问题 (Optimal Transport)。
9.2.2 光的搬运工
现在,请把“泥土”换成“光能量”。
- 乱土堆 = 经过病理角膜后,扭曲、强弱不均的光线波前。
- 防御工事 = 视网膜上那个完美、清晰、能量集中的像点。
- 铲子 = 自由曲面镜片。
蒙日-安培方程就是那个指挥铲子的包工头。它告诉我们:
“如果你想把这里的光能量(强度 )搬运到那里(强度 ),你的镜片表面必须拥有特定的曲率。”
用数学语言说,就是:
(严格公式:)
直觉瞬间: - 如果某处光线太散(光强太弱),方程命令镜片表面:“变凸一点!把周围的光聚过来!”
- 如果某处光线太密(光强太强),方程命令镜片表面:“变凹一点!把光散开!”
通过这种像素级的精细调节,我们不仅仅是在矫正视力,我们是在重塑光场的能量分布。
9.3 临床实战:当泪液成为透镜
对于巩膜镜,光学会算还不够,Dr. X 最担心的是生理耐受性。
泪液层是极好的液体透镜(折射率 1.336),能填平角膜的不规则。但它也是一把双刃剑:
- 太厚 (>400um):氧气传不过去,角膜水肿。
- 太薄 (<50um):镜片摩擦角膜,上皮脱落。
9.3.1 200微米的艺术
我们的目标是:无论角膜下面长得多么崎岖(甚至是 PMD 那种“接吻鸟”状的悬崖峭壁),镜片后表面必须像一层皮肤一样,以此为基础仅仅抬高 200微米。
这意味着,镜片后表面本身必须是一个复杂的自由曲面,它必须“模仿”角膜的病理形态,但又要足够光滑以保证光学性能。
这在传统工艺里是不可能的,但在 Wolfram 的计算世界里,这只是一个带约束的方程求解。
9.4 Wolfram 代码:设计你的第一枚“完美透镜”
我们要写一段代码,输入患者的地形图,输出一枚完美的巩膜镜参数。
我们遵循“黑箱先行”原则——你不需要懂偏微分方程的数值解法,你只需要看懂输入和输出。

代码解读
当你按下 Shift+Enter:
- 初始化:程序先生成一个完全平行于病理角膜的镜片。
- 冲突:此时泪液层完美均匀,但光学很差(因为镜片表面也是坑坑洼洼的)。
- MA 迭代:方程开始工作。它稍微抹平镜片表面的坑洼以改善光学,但又小心翼翼地不让泪液层变得太厚或太薄。
- 结果:你会得到一个形状奇特的镜片(既不是球面也不是非球面),但它能奇迹般地同时让患者看得清、戴得舒服。
9.5 案例解析:透明边缘变性 (PMD) 的“反马鞍”
Dr. X,PMD 患者的地形图是最棘手的,典型的“接吻鸟”或“蟹爪”图形。
在微分几何里,这意味着下方角膜是一个双曲点 (Hyperbolic Point) ——就像马鞍一样,水平方向是凸的,垂直方向却是平甚至凹的。
传统镜片的失败:
如果你用旋转对称的镜片,必然会在上方留出一个巨大的泪液蓄水池(雾视),而在下方压迫角膜突起(染色)。
MA 方程的解(反马鞍):
我们的计算结果会生成一个 “反马鞍” 形态的镜片后表面:
- 在角膜凸起的地方,镜片主动“让开”(变凹)。
- 在角膜平坦的地方,镜片主动“贴近”(变平)。
这种设计在几何上被称为 拓扑互补 (Topological Complementarity)。只有通过蒙日-安培方程的逐点计算,机床才能切削出这种违反直觉但符合逻辑的形状。
9.6 结语:从“试错”到“数字孪生”
Dr. X,本章可能是整本书里数学密度最高的一章,但请记住它的临床意义:
它终结了试戴片时代。
当你掌握了蒙日-安培方程,你就不再是一个在那儿反复换镜片、碰运气的验光师。
你扫描角膜,你设定目标(200um 泪液层 + 1.0 视力),然后你按下“Enter”。
剩下的,交给数学。
现在,我们已经解决了光学(第8章)和形状(第9章)的问题。在全书的最后乐章(第10章),我们将把所有这些——波前、流形、算法——融合在一起,构建一个患者眼球的完整数字孪生 (Digital Twin)。
准备好了吗?最后一步跨越即将到来。
