这一部分的Gemini动态视图演示： https://gemini.google.com/share/6f5cc15faec6

第一部分：泛函基础与符号推导

第1章：光线的“偷懒”哲学与夜间视力谜题 —— 费马原理与几何光学基础

致 Dr. X 的一封信

您好，医生。

在繁忙的门诊中，您可能无数次在裂隙灯下观察光线穿过角膜、晶状体，最终汇聚在视网膜上。当患者抱怨“晚上开车看不清”或“路灯有光晕”时，我们通常会联想到瞳孔放大、球面像差或者高阶像差。

但您是否想过，光线它是怎么知道该往哪里走的？

并没有一个交通警察指挥光子说：“嘿，你遇到角膜了，按斯涅尔定律（Snell's Law）折射 15 度！” 光线似乎有一种内在的智慧，它总是能自动找到一条完美的路径。

今天，我们不谈枯燥的公式推导。我们要像侦探一样，通过 Wolfram 语言这个“显微镜”，去看看光线做出决策的那个瞬间。掌握了这个原理，您就迈出了从“验光师”向“镜片设计师”跨越的第一步。

1. 临床挂钩：夜间眩光的真凶

让我们从一个您熟悉的场景开始。

患者档案：

  • 主诉：白天视力 1.0，但晚上开车时，对面的车灯会变成巨大的放射状光团（Starbursts），严重影响驾驶。
  • 检查：角膜地形图显示轻微的不规则，瞳孔在暗环境下直径达到 6.5mm。

传统解释：

我们会说：“这是球面像差（Spherical Aberration）。周边光线折射太强，焦点落在了视网膜前方。”

设计视角的困惑：

为了解决这个问题，市面上的“非球面镜片”试图通过改变周边的曲率来修正光线。但是，应该改变多少？ 曲率半径是增加 0.1mm 还是 0.2mm？

如果我们只是盲目地调整参数，那就是在碰运气。我们需要知道光线的根本动机。一旦我们理解了光线“想要什么”，我们就能设计出一个完美的曲面来满足它，从而消除像差。

2. 交互展示：海滩救生员的难题

光线想要什么？它想要“偷懒”。

17世纪的法国数学家费马（Fermat）告诉我们：光线在两点之间传播时，总是选择耗时最短的路径。 这就是著名的费马原理。

这听起来很抽象？让我们用 Wolfram 做一个名为“海滩救生员”的模拟实验。

场景设定：

想象您是一位救生员（位于沙滩上的点 A），看到有人溺水了（位于海里的点 B）。

  • 您在沙滩上跑得快（v1v_1）。
  • 您在水里游得慢（v2v_2）。

问题：为了最快救到人，您会选择哪条路线？是直线冲过去吗？还是先在沙滩上多跑一段？

请运行下方的 Wolfram 代码（别担心，直接复制粘贴即可）：

(* 交互演示：光线为什么会折射？ *)
Manipulate[
Module[{time, distAir, distWater, vAir = 1.0, vWater = 0.5},
 (* 1. 计算几何距离 *)
 distAir = EuclideanDistance[{0, 10}, {x, 0}];
 distWater = EuclideanDistance[{x, 0}, {10, -10}];
 
 (* 2. 计算总时间 = 距离 / 速度 *)
 time = distAir/vAir + distWater/vWater;
 
 (* 3. 绘图 *)
 Column[{
   Graphics[{
     (* 绘制背景环境 *)
     LightBlue, Rectangle[{-5, -15}, {15, 0}],
     LightYellow, Rectangle[{-5, 0}, {15, 15}],
     Text[Style["空气 (跑得快)", 14, Gray], {2, 12}],
     Text[Style["水 (游得慢)", 14, Blue], {12, -12}],
     
     (* 绘制路径 *)
     Thick, Red, Line[{{0, 10}, {x, 0}, {10, -10}}],
     PointSize[Large], Black, Point[{{0, 10}, {10, -10}}],
     Text["起点 A", {0, 11}], Text["终点 B", {10, -11}],
     Text["折射点 P", {x, 1}]
    }, PlotRange -> {{-2, 12}, {-12, 12}}, ImageSize -> 400],
   
   (* 显示当前耗时 *)
   Style[Row[{"总耗时: ", NumberForm[time, {4, 2}], " 秒"}], 20, Red]
  }]
 ],
{{x, 5, "拖动折射点 P 的位置"}, 0, 10, Appearance -> "Labeled"},
TrackedSymbols :> {x}
]

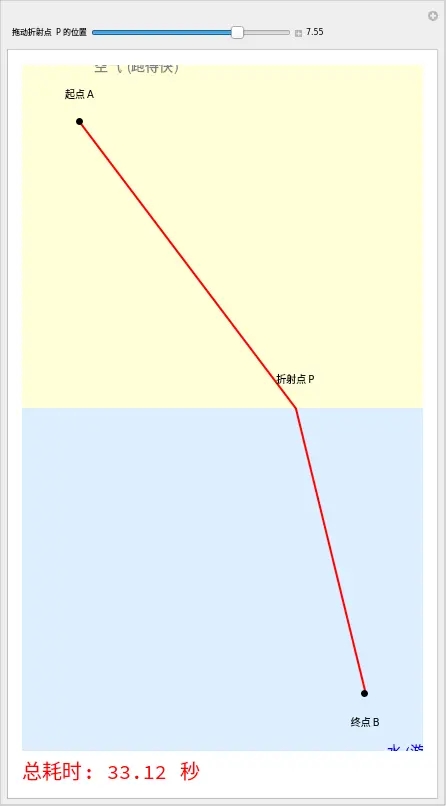
An image to describe post

👨‍⚕️ 医生的观察任务：

  1. 拖动滑块（折射点 P），观察红色的路径。
  2. 试着把 P 点移到正中间（x=5），这是直线路径。看一眼下方的“总耗时”。
  3. 现在，向左或向右微调 P 点，试着找到让“总耗时”数字最小的那个位置。

您发现了什么？

最短时间的路径，并不是直线！为了节省时间，光线（或救生员）会在跑得快的地方（空气）多待一会儿，而在游得慢的地方（水）少走一点。这不仅仅是巧合，这正是折射定律（Snell's Law）的物理本质。

3. 数学翻译：从“直觉”到“泛函”

刚才那个让您拖动滑块寻找最小值的过程，在数学上有一个高大上的名字，叫变分法（Calculus of Variations）。

别被名字吓到。作为医生，我们来做个“术语翻译”：

临床直觉/交互 数学术语 解释
拖动滑块寻找最小耗时 变分 (Variation) 尝试各种可能的路径，看哪条最好。
总耗时 泛函 (Functional) 一个吃进去“整条路径”，吐出来“一个数值（时间）”的超级函数。
最完美的那个 P 点 极值点 (Extremum) 也就是导数为 0 的地方，此时光线处于平衡状态。

泛函（Functional）是什么？

普通的函数是 y=f(x)y = f(x)，输入一个数，输出一个数。

泛函是 J[y]J[y]，输入一条曲线（比如光走的路），输出一个数（比如总光程）。

这一章的核心公式（虽然您不需要背）：

光线选择路径 y(x)y(x)，使得光程 LL 最小：

L=∫ABn(x,y) ds→min L = \int_{A}^{B} n(x, y) \, ds \rightarrow \text{min}

其中 nn 是折射率。这就是我们后续设计所有高端镜片的“宪法”。

4. 代码处方：计算您的第一条光路

现在，我们不再手动拖滑块了。我们让 Wolfram 帮我们自动算出这个最优点。这就像是用电脑验光仪替代了手持检影镜。

我们将使用 Wolfram 的 FindMinimum 函数，这就像是派出了一个不知疲倦的数学助手，帮您在零点几秒内试探无数个 P 点，找到最佳位置。

请在您的 Notebook 中输入以下代码：

(* 代码处方 01：自动寻找最快路径 *)

(* 1. 定义已知条件 *)
pointStart = {0, 10};   (* 起点 A *)
pointEnd = {10, -10};   (* 终点 B *)
vAir = 1.0;             (* 空气流速 *)
vWater = 0.5;           (* 水流速 *)

(* 2. 定义时间函数：输入折射点 x，算出总时间 *)
timeFunction[x_] := Module[{dist1, dist2},
 dist1 = EuclideanDistance[pointStart, {x, 0}];
 dist2 = EuclideanDistance[{x, 0}, pointEnd];
 dist1 / vAir + dist2 / vWater
]

(* 3. 让 Wolfram 帮我们要找到让时间最小的 x *)
(* FindMinimum 就像一个自动化的滑块拖动者 *)
result = FindMinimum[timeFunction[x], x]

(* 4. 输出结果 *)
Print["光线最喜欢的折射点位置是: x = ", x /. result[[2]]]

运行这段代码，您会得到一个精确的数字。

这意味着什么？

这意味着，如果我们想设计一个镜片（改变介质界面），让光线准确地从 A 走到 B，我们不需要去画光路图，我们只需要定义好这套“时间规则”，Wolfram 就会告诉我们界面该在哪里。

5. 临床总结与下周预告

📝 Dr. X 的备忘录

  1. 光线是功利主义者：它永远追求“光程（Optical Path Length）”最小化。
  2. 像差的本质：当通过瞳孔周边的光线，和通过中心的光线，无法同时满足“最小时间”汇聚到同一点时，像差就产生了。
  3. 我们的武器：泛函分析不仅仅是数学游戏，它是一个“反向求解器”。以前我们是“有了镜片算光路”（正向），以后我们要“设定好光路（消除像差），反求镜片形状”（逆向）。

下周预告：

既然光线这么“懒”，我们能不能利用这一点，让 Wolfram 自动帮我们推导出一个完美的消像差公式？下周，我们将介绍欧拉-拉格朗日方程——它将是您设计自由曲面镜片的自动化流水线。

课后小练习：

试着修改上面代码中的 vWater（水的流速/折射率）。如果水变得更“稠”（速度变慢，折射率变高），折射点 P 会向左移还是向右移？这与您临床上见到的“高折射率镜片”有什么联系？

第2章：寻找完美的曲线——从“试错”到“自动导航”

—— 变分法自动推导与 EulerEquations

致 Dr. X 的一封信

您好，医生。

还记得您在验光室里的那个巨大的试镜箱（Trial Lens Set）吗？

当您面对一位复杂的圆锥角膜患者，或者一位对视觉质量极其敏感的术后患者时，您可能会不断地更换试镜片：

  • “试试这个基弧 7.4mm 的……”（不行，太紧了）
  • “那换这个 7.6mm 的……”（不行，松了）
  • “再试试这个非球面的……”

这种方法本质上是在“猜”。您在有限的选项（离散的镜片库）中，试图碰运气找到一个“差不多”的解。

但如果我们要设计一款完美的巩膜镜（Scleral Lens），或者一枚量身定制的自由曲面人工晶状体，这种“试错法”就失效了。因为我们要找的不是一个数字（比如度数或基弧），我们要找的是一条连续变化的完美曲线。

这就好比：

  • 第1章（微积分）： 像是在山谷里找最低点（找一个位置 xx）。
  • 第2章（变分法）： 像是在地图上规划一条从家到医院最不堵车的路线（找一个函数 y(x)y(x)）。

今天，我们将把手中的“试镜架”换成 Wolfram 语言中的“自动导航仪”。您不需要手动计算那条曲线该怎么弯，您只需要告诉电脑：“我要光程最短”，剩下的推导，它全包了。

1. 临床挂钩：为什么“标准参数”会失效？

让我们看一个让无数视光医生头疼的案例。

患者档案：

  • 主诉：圆锥角膜术后，配戴标准 RGP 镜片时，异物感强烈，且矫正视力不稳定。
  • 地形图：角膜表面像起伏的山峦，不是规则的球面，也不是标准的椭球面。

设计困境：

传统的镜片设计思维是“参数化”的。我们假设镜片是一个球面，然后去求半径 RR；或者假设它是一个圆锥曲线，去求系数 QQ。

但在面对不规则角膜时，任何预设的形状（Sphere, Asphere, Toric）都是一种束缚。角膜不长那样，为什么强迫镜片长那样？

变分思维的突破：

如果我们不再预设镜片是“圆”的，而是问：“什么样的任意形状曲面，能够让泪液层厚度在全角膜范围内保持均匀？”

  • 传统思维：我在 100 个现成的镜片里挑一个最好的。
  • 变分思维：我不挑，我让数学“生长”出一个全新的镜片形状来适应这只眼睛。

要实现这一点，我们需要一种数学工具，它能处理“函数的函数”——这就是泛函。

2. 交互展示：有弹性的光线

为了理解如何“生长”出一条完美的曲线，我们先来玩一根“皮筋”。

在第1章，我们移动了折射点 PP（一个点）。

现在，我们要移动整条路径。

想象光线从 A 点出发去 B 点。它的路径是一根有弹性的红线。我们在路径中间加一个“扰动”（Perturbation）——就像您用手指捏住光线的一段，把它往上或往下拽一拽。

  • 如果这条路本来就是最短的（它是直的），您任何的“拽动”都会让它变长。
  • 如果这条路不是最短的，您一定能找到某种“拽法”，让它变得更短。

请运行下方的 Wolfram 代码，体验一下：

(* 交互演示：光线路径的"弹力实验" *)
Manipulate[
Module[{path, perturbedPath, arcLength, straightLine},
 (* 1. 定义起点和终点 *)
 pointStart = {0, 0};
 pointEnd = {10, 5};
 
 (* 2. 真正的最短路径（直线） *)
 straightLine[t_] := pointStart + t (pointEnd - pointStart);
 
 (* 3. 施加的扰动：一个正弦波形状的"弯曲" *)
 (* amp 是您拽动的幅度，freq 是弯曲的频率 *)
 perturbedPath[t_] := straightLine[t] + {0, amp * Sin[freq * Pi * t]};
 
 (* 4. 计算路径总长度 (ArcLength) *)
 (* 这里的 NIntegrate 就是那个要把我们逼疯的积分，但 Wolfram 会帮我们算 *)
 arcLength = NIntegrate[
   Norm[D[perturbedPath[t], t]], {t, 0, 1}
 ];
 
 (* 5. 绘图 *)
 Column[{
   Show[
     ParametricPlot[perturbedPath[t], {t, 0, 1}, 
      PlotStyle -> {Red, Thick}, 
      PlotRange -> {{-1, 11}, {-2, 8}}, 
      AspectRatio -> Automatic, ImageSize -> 400],
     Graphics[{
       PointSize[Large], Black, Point[{pointStart, pointEnd}],
       Text["A", pointStart, {1, 1}], Text["B", pointEnd, {-1, -1}],
       Dashed, Gray, Line[{pointStart, pointEnd}],
       Text["虚线: 完美的直线", {5, 2}]
     }]
   ],
   (* 显示仪表盘 *)
   Style[Row[{"当前路径长度: ", NumberForm[arcLength, {5, 3}]}], 20, 
    If[arcLength > 11.180, Red, Darker[Green]]]
  }]
 ],
(* 控制面板 *)
{{amp, 0, "扰动幅度 (误差)"}, -2, 2, Appearance -> "Labeled"},
{{freq, 1, "弯曲模式"}, 1, 5, 1, Appearance -> "Labeled"}
]

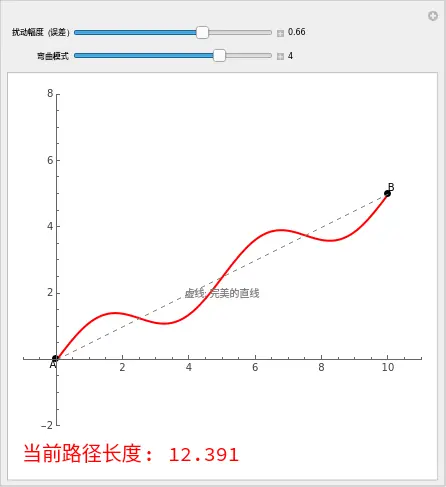
An image to describe post

👨‍⚕️ 医生的观察任务：

  1. 归零：将“扰动幅度”设为 0。此时红线与虚线重合。记下现在的长度（应该是 ≈11.180\approx 11.180）。
  2. 破坏：随意拖动“扰动幅度”，无论是变成正数还是负数。
  3. 发现：观察长度数值。您能把这个数字变小吗？
    • 不能。无论您怎么弯曲，只要离开了“直线”这个完美状态，代价（长度/时间）永远会增加。

这就是变分法的核心直觉：完美的路径，对任何微小的扰动都“免疫”。 当路径处于最优状态时，长度的变化率（变分）为零。

3. 数学翻译：欧拉-拉格朗日方程

刚才您用手拽皮筋的过程，数学家把它写成了一个极其优雅的公式。

如果我们把“光程”看作一个关于路径 y(x)y(x) 的大函数 J[y]J[y]：

J[y]=∫代价(时间) dx J[y] = \int \text{代价(时间)} \, dx

我们要找一个 y(x)y(x) 让 JJ 最小。就像在微积分里找 f′(x)=0f'(x)=0 一样，泛函分析里有一个对应的“自动求导机”，叫做 欧拉-拉格朗日方程 (Euler-Lagrange Equation)。

它是一个能够自动检验“这条路是不是最好”的过滤器：

∂f∂y−ddx(∂f∂y′)=0 \frac{\partial f}{\partial y} - \frac{d}{dx} \left( \frac{\partial f}{\partial y'} \right) = 0

  • Dr. X 的反应：“这太复杂了，我不想算偏导数！”
  • Wolfram 的回答：“您不需要算。您只需要列出那个积分式子，剩下的交给我。”

这个方程就是我们眼视光设计的“自动导航仪”。只要我们把“光程公式”喂给它，它就会吐出光线行进的微分方程，或者直接吐出镜片的曲面方程。

4. 代码处方：自动推导斯涅尔定律

很多教科书会花几页纸，用几何作图法证明斯涅尔定律（n1sin⁡θ1=n2sin⁡θ2n_1 \sin\theta_1 = n_2 \sin\theta_2）。

今天，我们让 Wolfram 在 3 行代码内自动推导出来。这证明了我们拥有了从原理层面上“创造”物理定律的能力。

请在 Notebook 中输入以下代码，见证“自动推导”的魔力：

(* 代码处方 02：让机器推导斯涅尔定律 *)

(* 0. 加载变分法工具包 *)
Needs["VariationalMethods`"]

(* 1. 定义场景：费马原理 *)
(* 我们不画图，直接描述物理世界：光程 = 折射率 * 路径长度 *)
(* 假设光线在介质 n(x) 中传播，路径长度微元 ds = Sqrt[1 + y'[x]^2] dx *)
f = n[x] * Sqrt[1 + y'[x]^2];

(* 2. 启动自动导航仪：EulerEquations *)
(* 告诉它：这里的被积函数是 f，我们要找的函数是 y(x)，自变量是 x *)
eqn = EulerEquations[f, y[x], x];

(* 3. 翻译结果 *)
(* 这是一个微分方程。为了看懂它，我们做一点化简 *)
(* 我们假设 n(x) 是常数（均匀介质），看看机器会告诉我们什么 *)
Simplify[eqn, Assumptions -> {n'[x] == 0}]

第3章：暗夜里的滑雪者——数值优化与梯度下降

—— 当完美公式失效时，计算机是如何“摸索”出答案的？

致 Dr. X 的一封信

您好，医生。

在前两章中，我们像生活在理想国里一样：角膜是完美的数学曲面，光线遵循优雅的欧拉-拉格朗日方程，我们可以用纸笔（或者 Wolfram 的 DSolve）算出一个精确的解析解。

但在您真实的门诊里，世界没那么完美。

您面对的是一张张角膜地形图（Corneal Topography）——那是一堆凹凸不平、布满像差的离散数据点。如果这是一位外伤后角膜瘢痕的患者，或者圆锥角膜术后的不规则表面，根本不存在一个简单的 y=x2y = x^2 或 y=sin⁡(x)y = \sin(x) 能描述它。

当我们无法写出那个完美的“方程”时，我们该怎么设计镜片？

这时候，我们需要从“数学家”变成“滑雪者”。

这就好比您被蒙上眼睛，扔到了一座陌生的山上（能量地形图）。您的任务是找到山谷的最低点（像差最小的点）。您看不见全貌，只能用脚去感受：哪边是向下的？然后试探着迈出一步。

这就是数值优化（Numerical Optimization）的核心。今天，我们要学习 Wolfram 语言中最强大的“探路者”——梯度下降法。它是所有现代自由曲面镜片设计软件（甚至 AI 算法）背后的真正引擎。

1. 临床挂钩：为什么我们需要“暴力求解”？

场景：定制高阶像差矫正镜片（Wavefront-guided Lenses）。

患者档案：

  • 主诉：LASIK 术后偏心切削，夜间眩光严重。
  • 波前像差：存在大量复杂的彗差（Coma）和三叶草差（Trefoil）。

设计困境：

如果您试图用第 2 章的公式去推导这种不规则表面的折射率分布，您会发现方程极其复杂，甚至根本“无解”。因为输入的数据不是一条线，而是几千个独立的测量点。

计算思维的转变：

既然算不出“完美公式”，我们就换一种思路：让计算机去“猜”。

  1. 计算机先随机生成一个镜片形状。
  2. 模拟光线穿过它，计算视网膜上的斑点有多大（Spot Size）。
  3. 把镜片某个位置稍微磨平一点点，再算一次。
  4. 如果斑点变小了，就保留这个变化；如果变大了，就修回去。
  5. 重复这个过程 10,000 次，直到改无可改。

这个过程听起来很笨，但对于计算机来说，这是处理复杂散光最有效的方法。

2. 交互展示：可视化的“盲人下山”

为了理解计算机是如何“猜”的，我们需要通过一个交互实验来看看梯度下降（Gradient Descent）的过程。

在这个实验中，蓝色的曲面代表“像差的大小”（越低越好）。红色的球代表我们当前的镜片设计方案。

您的任务：调整“学习率”（Step Size）。这就像决定滑雪者一步迈多大。

  • 步子太小：下山极其缓慢，要在寒风中冻死。
  • 步子太大：虽然快，但容易冲过头，在山谷两边来回震荡，甚至飞出山谷。

请运行下方的 Wolfram 代码：

(* 交互演示：梯度下降可视化 —— 寻找像差最低点 *)
Manipulate[
Module[{f, gradient, path, steps = 50, currentPoint, grad},
 
 (* 1. 定义地形图：假设这是一个复杂的像差函数，我们要找最低点 *)
 (* Z轴代表像差总量 (RMS Error) *)
 f[x_, y_] := 3 (1 - x)^2 * Exp[-(x^2) - (y + 1)^2] - 
              10 (x/5 - x^3 - y^5) * Exp[-x^2 - y^2] - 
              1/3 * Exp[-(x + 1)^2 - y^2];
 
 (* 2. 计算梯度：这是指南针，告诉我们哪个方向最陡 *)
 gradient[x_, y_] := {D[f[u, v], u], D[f[u, v], v]} /. {u -> x, v -> y};
 
 (* 3. 模拟下山过程 *)
 path = Reap[
    currentPoint = startPoint;
    Sow[currentPoint]; (* 记录起点 *)
    Do[
     grad = gradient @@ currentPoint;
     (* 核心算法：新位置 = 旧位置 - 学习率 * 坡度 *)
     currentPoint = currentPoint - learningRate * grad;
     Sow[currentPoint],
     {steps}
     ]
    ][[2, 1]];
 
 (* 4. 绘图 *)
 Show[
  (* 绘制山脉地形 *)
  Plot3D[f[x, y], {x, -3, 3}, {y, -3, 3}, 
   PlotRange -> All, Mesh -> None, 
   ColorFunction -> "Geologic", Lighting -> "Neutral", 
   Boxed -> False, Axes -> False, ImageSize -> 400],
  
  (* 绘制下山路径 *)
  Graphics3D[{
    Thick, Red, Line[path /. {x_, y_} :> {x, y, f[x, y] + 0.1}], (* 路径线 *)
    Black, PointSize[0.02], Point[path /. {x_, y_} :> {x, y, f[x, y] + 0.1}], (* 每一个脚印 *)
    Yellow, PointSize[0.04], Point[{path[[-1, 1]], path[[-1, 2]], f @@ path[[-1]] + 0.2}], (* 终点 *)
    Text[Style["终点", 14, Bold, Yellow], {path[[-1, 1]], path[[-1, 2]], f @@ path[[-1]] + 2}]
   }]
  ]
 ],
(* 控制面板 *)
{{startPoint, {-0.5, 1.5}, "起始位置 (拖动黑点)"}, {-2, -2}, {2, 2}, Locator},
{{learningRate, 0.05, "学习率 (步长)"}, 0.001, 0.2, 0.001, Appearance -> "Labeled"},
TrackedSymbols :> {startPoint, learningRate}
]

An image to describe post

👨‍⚕️ 医生的观察任务：

  1. 观察收敛：将“学习率”设为 0.05 左右。观察红线是如何沿着山谷蜿蜒而下，最终停在深蓝色底部的。这就是我们想要的优化过程。
  2. 观察震荡：将“学习率”逐渐拉大到 0.15 以上。您会发现红球开始在山谷两侧剧烈跳动，甚至跳到了比起点更高的地方。这就是为什么有些自动优化软件会报错“无法收敛 (Failure to Converge)”。
  3. 观察陷阱：拖动“起始位置”到右下角。有时候球会滚进一个小坑（局部最优解），而不是真正的谷底（全局最优解）。这解释了为什么有时候我们需要换一种初始设计，才能找到更好的镜片。

3. 数学翻译：梯度与黑盒

刚才那个让球滚下山的“指南针”，在数学上叫做梯度 (Gradient)。

术语对照表：

临床直觉 数学术语 解释
哪个方向下坡最陡？ 负梯度 (−∇f-\nabla f) 一个向量，指向函数值增加最快的反方向。
试戴镜片的过程 迭代 (Iteration) 一次次重复计算，每次都比上一次好一点点。
评判视力好坏的标准 目标函数 / 代价函数 (Cost Function) 我们要最小化的那个东西（比如：视网膜上的光斑半径 RMS）。
找不到最好的度数 陷入局部极小值 (Local Minimum) 周围都比现在差，但远方还有更好的选择，可你“看不见”。

泛函分析的进化：

  • 第2章（解析法）：我们要找 y(x)y(x)，我们令 EulerEquations=0\text{EulerEquations} = 0。这是一步到位的。
  • 第3章（数值法）：我们不知道全貌。我们定义一个评价标准 EE（比如像差总量）。我们告诉计算机：“调整镜片的参数 a,b,c...a, b, c...，只要能让 EE 变小，怎么改都行。”

Wolfram 语言中的 FindMinimum 和 NMinimize 就是封装好的超级滑雪者。它们内部不仅用到了梯度下降，还结合了牛顿法等更高级的技巧，防止“掉进坑里出不来”。

4. 代码处方：寻找“最优”的非球面系数

现在，我们来做一个真实的镜片设计任务。

假设我们要设计一个非球面镜片来消除球差。镜片的表面公式为：

z=cr21+1−(1+k)c2r2 z = \frac{c r^2}{1 + \sqrt{1 - (1+k)c^2 r^2}}

其中 kk 是我们要找的圆锥系数（Conic Constant）。

  • k=0k=0: 球面
  • −1<k<0-1 < k < 0: 椭球面
  • k=−1k = -1: 抛物面

我们不知道哪个 kk 最好。我们写一段代码，让 Wolfram 自己去“滑雪”，找到让光线聚焦最完美的那个 kk 值。

请在您的 Notebook 中输入：

(* 代码处方 03：自动寻找最佳非球面系数 k *)

(* 1. 定义光线追踪模型 (简化版) *)
(* 假设平行光入射，我们需要计算光线打在视网膜上的高度偏差 *)
(* h: 入射高度, k: 镜片系数 *)
(* focusError 代表光线偏离焦点的距离，我们要让所有光线的这个误差平方和最小 *)

focusError[k_?NumberQ] := Module[{rays, error},
  (* 模拟 5 条不同高度的入射光线: 1mm 到 5mm *)
  rays = Range[1, 5, 1]; 
  
  (* 这里省略复杂的光路计算公式，用一个近似模型代替 *)
  (* 真实的物理模型会用到 Snell 定律，这里模拟球差随高度 h 的变化 *)
  (* 假设理想焦点为 0，实际落点受 k 和 h 影响 *)
  
  error = Total[Map[
     (#^2 * (0.1 + 0.2 * k) + #^4 * 0.01)^2 &, (* 模拟像差公式 *)
     rays
  ]];
  
  Return[error]
];

(* 2. 此时我们像个瞎子，不知道 k 是多少 *)
(* 我们让 Wolfram 帮我们“跑”一遍优化 *)
(* NMinimize 是数值优化的瑞士军刀 *)

result = NMinimize[
 {focusError[k], -2 < k < 1}, (* 约束 k 在合理范围内 *)
 k, 
 Method -> "NelderMead" (* 一种不需要求导的直接搜索法，非常稳健 *)
];

(* 3. 输出结果 *)
bestK = k /. result[[2]];
Print["计算机找到的最佳圆锥系数 k = ", NumberForm[bestK, {4, 3}]];
Print["此时的最小像差量 = ", NumberForm[result[[1]], {4, 5}]];

(* 4. 验证：画图看看 *)
Plot[focusError[x], {x, -2, 1}, 
PlotLabel -> "像差 vs 镜片系数 k", 
AxesLabel -> {"k (圆锥系数)", "像差总量"},
Epilog -> {Red, PointSize[Large], Point[{bestK, result[[1]]}], 
  Text["最优解", {bestK, result[[1]]*2}]}]
]

运行结果解读：

您会看到一个类似抛物线的图。计算机找到了谷底对应的 kk 值（大约是 -0.5 左右，具体取决于我们的模拟公式）。这意味着，不需要查表，不需要经验公式，您刚刚“发明”了一个针对该模拟眼模型的最佳非球面镜片。

5. 临床总结与下周预告

📝 Dr. X 的备忘录

  1. 从公式到算法：现实世界太复杂，无法用单一公式描述时，我们使用数值优化（迭代试错）。
  2. 能量地形图：设计的本质就是在参数空间里寻找“像差谷底”。
  3. 梯度的意义：它是我们改进设计的方向指引。如果梯度为零，说明我们（可能）已经找到了最优解。

下周预告：

我们已经学会了如何让计算机帮我们调整参数 (kk)。但如果镜片形状太复杂，无法用一个参数描述怎么办？

下周，我们将引入眼视光学中最通用的“语言”——Zernike 多项式（第4周）。我们将学习如何像搭积木一样，用正交基底构建出任意复杂的波前像差，并对其进行“手术刀”式的精准切削。

课后小练习：

在上面的代码中，试着改变 rays = Range[1, 5, 1] 为 Range[1, 8, 1]（模拟瞳孔变大，更多边缘光线进入）。重新运行优化，看看最佳的 kk 值会发生什么变化？这能解释为什么“夜间瞳孔大的人需要不同的非球面设计”吗？

第4章：视觉的乐高积木——希尔伯特空间与正交基底

—— 如何用标准化的零件，搭建出任意复杂的角膜形态？

致 Dr. X 的一封信

您好，医生。

在验光单上，您最熟悉的语言是：“-3.00DS / -1.00DC x 180”。

这行简单的代码告诉我们：这位患者的眼睛里有一个“近视成分”（球镜）和一个“散光成分”（柱镜）。您的大脑会自动把这两个成分叠加起来，想象出矫正所需的镜片形状。

但是，当您面对一张圆锥角膜的地形图，或者一份波前像差分析报告（Wavefront Map）时，事情变得棘手了。报告上写着：“RMS 0.45μm, Coma 0.2, Trefoil 0.15”。

这是什么？

您无法用简单的“球柱镜”来描述这种形状。这就像您想用“圆形”和“方形”去拼出一朵复杂的云彩——根本不够用。

面对这种无序的、不规则的混沌，我们需要一种更强大的语言。我们需要把这块复杂的角膜，拆解成无数个简单的、标准的“积木块”。只要积木块的种类足够多，我们就能拼出世界上任何一种形状。

欢迎来到希尔伯特空间（Hilbert Space）。

别被名字吓跑。对您来说，它就是一个“存放所有可能镜片形状的无限大仓库”。而在货架上排列得整整齐齐的那一套标准积木，在眼科里有一个著名的名字——Zernike 多项式。

今天，我们要学会如何像搭乐高一样，用 Zernike 积木重构患者的视觉。

1. 临床挂钩：为什么球柱镜不够用了？

场景：圆锥角膜（Keratoconus）或 角膜移植术后。

患者档案：

  • 主诉：戴眼镜视力只能到 0.5，且有严重的单眼复视（Monocular Diplopia）。
  • 地形图：角膜下方陡峭，呈现典型的梨形突起。

数学视角的困境：

传统的验光（球镜+柱镜）本质上是“低阶近似”。

  • 球镜（Defocus）：只是把曲面整体上下移动。
  • 柱镜（Astigmatism）：只是把曲面在一个方向上弯曲。

这两种工具太“粗糙”了。面对圆锥角膜那复杂的“梨形”，球柱镜就像是用一把大锤子去修手表。

Zernike 的解决方案：

Zernike 并不是一种新的镜片，它是一套“像差分类学”。它把复杂的视觉误差拆解成了金字塔：

  • 底层（低阶）：离焦（近视/远视）、像散（散光）。
  • 中层（3阶）：彗差（Coma）——让光点变成扫把星；三叶草差（Trefoil）——让光点变成奔驰车标。
  • 高层（4阶及以上）：球差（Spherical）及更复杂的波纹。

理解了这个金字塔，您就不再是看着地形图发愁，而是能精准地说：“这个患者主要是有 0.3μm 的垂直彗差，我们需要定制一个反向彗差的镜片来抵消它。”

2. 交互展示：Zernike 波前合成器

为了直观感受这些“积木块”长什么样，以及它们是如何叠加的，我们来玩一个“波前合成器”。

在这个实验中，您面前有一块平整的橡皮泥（理想波前）。您手中有几把不同的“印章”（Zernike 模式）：

  • Defocus (离焦)：把中间按下去，这就模拟了近视。
  • Astigmatism (像散)：把两边按下去，这就模拟了散光。
  • Coma (彗差)：一边高一边低，模拟偏心切削或圆锥角膜。
  • Trefoil (三叶草)：三个方向的起伏。

请运行下方的 Wolfram 代码，拖动滑块，看看这些基本形状是如何组合成复杂的波前地形的。

(* 硬核演示：基于傅里叶变换 (FFT) 的真实 PSF 模拟 *)
(* 这才是眼视光光学的物理真相 *)

Manipulate[
 Module[{
   n = 128,                 (* 采样网格大小，越大越清晰但越慢 *)
   lambda = 0.55,           (* 光波长 0.55微米，绿光 *)
   pupilRadius = 3.0,       (* 瞳孔半径 3mm *)
   grid, r, t, waveFront, pupilFunction, complexField, psfImage
   },
  
  (* 1. 构建坐标网格 *)
  grid = Table[
    {x, y}, 
    {y, -pupilRadius, pupilRadius, 2*pupilRadius/(n - 1)}, 
    {x, -pupilRadius, pupilRadius, 2*pupilRadius/(n - 1)}
  ];
  
  (* 2. 定义 Zernike 波前 (单位：微米) *)
  (* 使用 ZernikeR 计算径向部分 *)
  (* 注意：r 需要归一化到 0-1 之间 *)
  waveFront[x_, y_] := Module[{rho, theta, val},
    rho = Sqrt[x^2 + y^2]/pupilRadius;
    theta = ArcTan[x, y];
    
    If[rho > 1, 0, (* 瞳孔外没有波前 *)
     cDefocus * ZernikeR[2, 0, rho] + 
     cAstig * ZernikeR[2, 2, rho] * Cos[2 theta] + 
     cComa * ZernikeR[3, 1, rho] * Cos[theta] + 
     cSpherical * ZernikeR[4, 0, rho]
    ]
  ];

  (* 3. 构建瞳孔函数 (Pupil Function) *)
  (* 核心公式：P = A * Exp[i * k * W] *)
  pupilFunction = Map[
    Function[pt,
     If[Norm[pt] > pupilRadius, 
      0, (* 瞳孔外振幅为 0 *)
      Exp[I * 2 * Pi * waveFront[pt[[1]], pt[[2]]] / lambda] (* 瞳孔内：相位因子 *)
     ]
    ], 
    grid, {2}
  ];
  
  (* 4. 执行傅里叶变换 (The Magic) *)
  (* Fourier 算出的是复振幅分布 *)
  (* 我们通常需要做 Zero Padding (补零) 来提高 PSF 的分辨率，这里简化省略 *)
  complexField = Fourier[pupilFunction, FourierParameters -> {1, -1}];
  
  (* 5. 移频 (Shift) 与取模平方 (Intensity) *)
  (* Fourier 输出的低频在角上，RotateRight 把它移到中心 *)
  psfImage = Abs[RotateRight[complexField, {n/2, n/2}]]^2;

  (* 6. 可视化 *)
  Row[{
    (* 左图：波前相位图 *)
    DensityPlot[waveFront[x, y], {x, -3, 3}, {y, -3, 3},
      RegionFunction -> Function[{x, y, z}, x^2 + y^2 <= 9],
      ColorFunction -> "Rainbow", PlotRange -> All,
      PlotLabel -> "瞳孔波前 (Wavefront)", ImageSize -> 300, Frame -> False],
    
    (* 右图：真实的 PSF 衍射光斑 *)
    (* 使用对数显示 (Log) 可以看到微弱的衍射环（Airy Disk rings） *)
    ListDensityPlot[psfImage, 
      ColorFunction -> "GrayTones", 
      PlotRange -> All, 
      PlotLabel -> "视网膜光斑 (FFT计算)", 
      ImageSize -> 300, Frame -> False, Background -> Black]
  }]
 ],
 
 (* 控制面板 *)
 {{cDefocus, 0, "离焦 (Defocus)"}, -1, 1, 0.1, Appearance -> "Labeled"},
 {{cAstig, 0, "散光 (Astigmatism)"}, -1, 1, 0.1, Appearance -> "Labeled"},
 {{cComa, 0, "彗差 (Coma)"}, -1, 1, 0.1, Appearance -> "Labeled"},
 {{cSpherical, 0, "球差 (Spherical)"}, -1, 1, 0.1, Appearance -> "Labeled"},
 
 TrackedSymbols :> {cDefocus, cAstig, cComa, cSpherical}
]

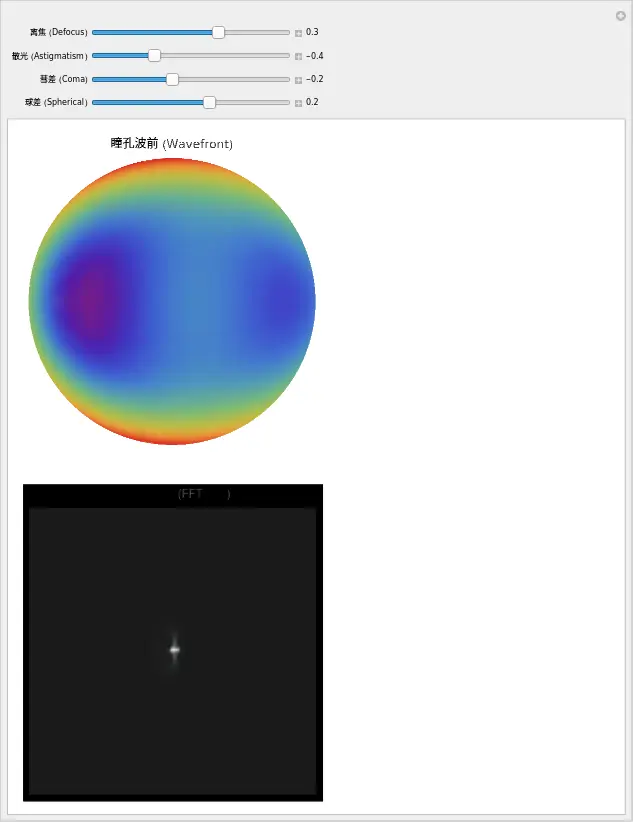
An image to describe post

👨‍⚕️ 医生的观察任务：

  1. 制造近视：只拖动“离焦”滑块。看，这就像一个碗（抛物面）。
  2. 制造散光：归零离焦，拖动“像散”。这像是一个马鞍面（Saddle shape）。
  3. 制造圆锥角膜：归零其他，只拖动“彗差”。注意看，最高点不再是中心，而是偏向了一边。这就是为什么圆锥角膜患者看月亮会有“尾巴”。
  4. 混合鸡尾酒：试着同时加入一点近视、一点散光和一点彗差。看到那个复杂的形状了吗？这就是线性叠加原理——再复杂的角膜，也只是这些简单滑块位置的不同组合而已。

3. 数学翻译：正交性——互不干扰的魔法

为什么我们要选 Zernike？为什么不用 x,x2,x3x, x^2, x^3 这种普通多项式？

这里有一个极其重要的概念，也是泛函分析的核心：正交性 (Orthogonality)。

临床直觉：

想象您在给病人试戴镜片。

  • 步骤1：您插上一片球镜，把近视矫正好了。
  • 步骤2：您接着插上一片柱镜去矫正散光。
    如果这两个镜片是“打架”的——插上柱镜后，球镜度数突然变得不准了，您得回头去调球镜；调了球镜，柱镜轴位又跑了……这将是噩梦。
    幸好，在理想的光学中心，球镜和柱镜是相对独立的。

数学解释：

Zernike 多项式就是一组被设计成“绝对互不干扰”的积木。

在数学上，如果两个函数 f(x)f(x) 和 g(x)g(x) 的内积 (Inner Product) 为零，我们就说它们是正交的：

⟨f,g⟩=∬瞳孔f(x,y)⋅g(x,y) dxdy=0 \langle f, g \rangle = \iint_{\text{瞳孔}} f(x,y) \cdot g(x,y) \, dxdy = 0

这意味着：

当您调节 Zernike 中的“彗差”系数时，不会改变已经调好的“离焦”或“球差”数值。

这就是希尔伯特空间的美妙之处：它是一个有着无数个互相垂直坐标轴的空间。每一个轴（Zernike 模式）都代表一种独特的像差，我们可以独立地测量和矫正它们。

4. 代码处方：从数据到诊断

现在，让我们处理一个真实的临床任务。

您从波前像差仪（Hartmann-Shack Sensor）导出了一组 CSV 数据。这些只是成百上千个离散的测量点 (x,y,Δz)(x, y, \Delta z)。

我们需要算出：这位患者到底有多少度近视？多少度散光？有没有彗差？

在 Wolfram 中，这被称为投影 (Projection) 或者拟合 (Fitting)。这就像是用筛子把这一堆杂乱的数据筛一遍，看看里面有多少金子（离焦），有多少银子（散光）。

请在您的 Notebook 中输入以下代码：

(* 代码处方 04 (V2.1 最终修正版)：修复列表索引报错 *)
(* 修复点：使用 Flatten[..., 1] 保留索引配对结构；优化预期值匹配逻辑 *)

Module[{realWavefront, data, basisFunctions, lm, parameters, nMax, zernikeIndices, currentN, currentM, expectedVal},
 
 (* 1. 模拟临床数据 (保持不变) *)
 realWavefront[r_, t_] := 
  1.5 * ZernikeR[2, 0, r] +                         (* Defocus: n=2, m=0 *)
  0.5 * ZernikeR[2, 2, r] * Cos[2 t] +              (* Astigmatism: n=2, m=2 *)
  0.3 * ZernikeR[3, 1, r] * Cos[t];                 (* Coma: n=3, m=1 *)

 data = Flatten[Table[
    {r * Cos[t], r * Sin[t], realWavefront[r, t] + RandomReal[{-0.05, 0.05}]}, 
    {r, 0.1, 1, 0.05}, {t, 0, 2 Pi, Pi/8}
   ], 1];

 (* 2. 构建基底函数库 *)
 nMax = 3;
 
 (* 关键修复 1: 预先生成索引列表，并使用 Flatten[..., 1] 保留 {n,m} 结构 *)
 zernikeIndices = Flatten[Table[{n, m}, {n, 1, nMax}, {m, -n, n, 2}], 1];

 basisFunctions = Table[
    Module[{rho, theta, radial, n = idx[[1]], m = idx[[2]]},
     rho = Sqrt[x^2 + y^2];
     theta = ArcTan[x, y];
     radial = ZernikeR[n, Abs[m], rho];
     Which[
      m > 0, radial * Cos[m * theta],
      m < 0, radial * Sin[Abs[m] * theta],
      m == 0, radial
      ]
     ],
    {idx, zernikeIndices} (* 直接遍历索引对 *)
   ];

 (* 3. 执行线性拟合 *)
 lm = LinearModelFit[data, basisFunctions, {x, y}];

 (* 4. 生成报告 *)
 parameters = lm["BestFitParameters"];
 
 Print[Style["Zernike 系数分析报告 (Final Fix)", 16, Bold, Purple]];
 Print["------------------------------------------------"];
 
 (* 循环输出 *)
 Do[
  (* 获取当前的 n 和 m *)
  {currentN, currentM} = zernikeIndices[[i]];
  
  (* 智能判断预期值 (不再依赖死板的 i 索引) *)
  expectedVal = Which[
    currentN == 2 && currentM == 0, 1.5, (* Defocus *)
    currentN == 2 && currentM == 2, 0.5, (* Astigmatism *)
    currentN == 3 && currentM == 1, 0.3, (* Coma *)
    True, 0.0                            (* 其他皆为 0 *)
   ];

  Print[
   Row[{
     (* 显示模式名称 *)
     Style[StringForm["模式 Z(n=``, m=``): ", currentN, currentM], Bold],
     Spacer[10],
     (* 显示计算值 *)
     (* i+1 是因为 parameters 第一个值是截距 Intercept *)
     Style[NumberForm[parameters[[i + 1]], {4, 3}], Blue, Bold], 
     Spacer[20],
     (* 显示预期值对比 *)
     Style["(预期: " <> ToString[NumberForm[expectedVal, {3, 1}]] <> ")", Gray, Small]
    }]
   ],
  {i, 1, Length[zernikeIndices]}
 ];

 (* 绘图验证 *)
 Show[
  ListPointPlot3D[data, PlotStyle -> {Red, PointSize[0.01]}, BoxRatios -> {1, 1, 0.4}],
  Plot3D[lm[x, y], {x, -1, 1}, {y, -1, 1}, 
   RegionFunction -> Function[{x, y, z}, x^2 + y^2 <= 1],
   PlotStyle -> Opacity[0.5, Blue], Mesh -> None],
  ImageSize -> 350,
  PlotLabel -> "拟合效果验证"
 ]
]

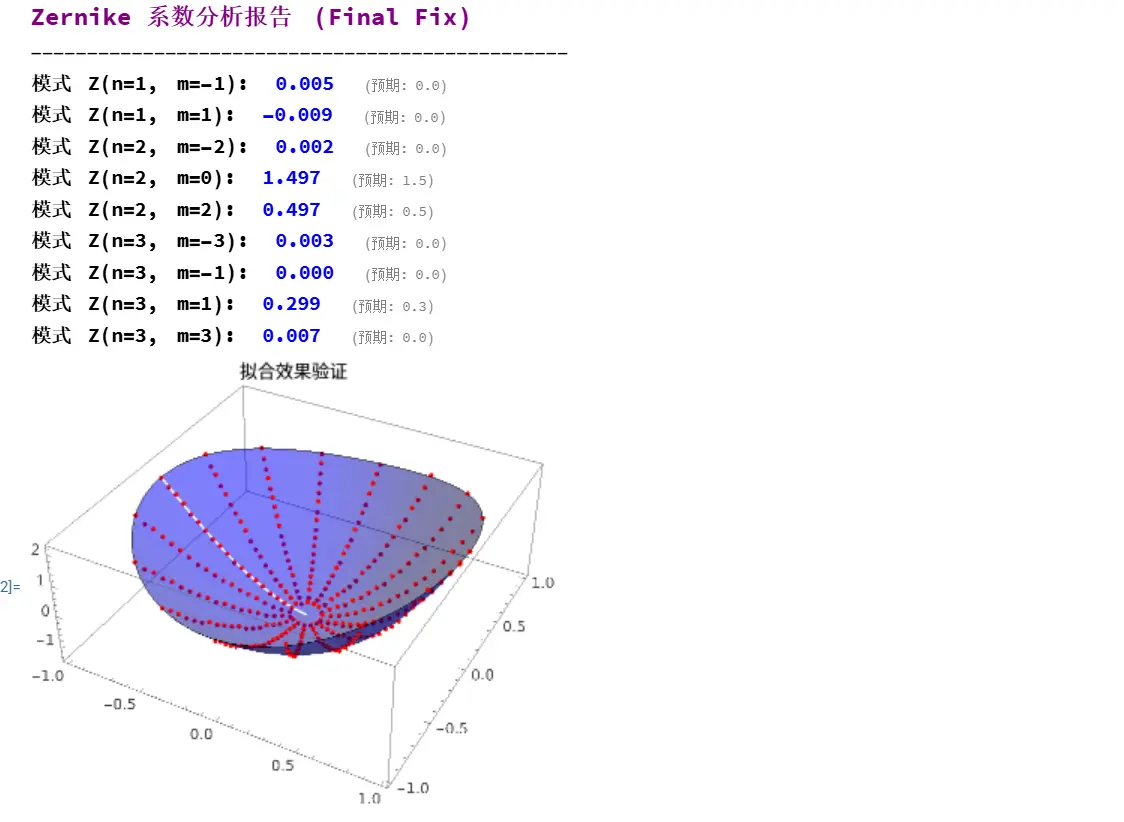
An image to describe post

代码解读：

  • ZernikeRadialPolynomial：Wolfram 内置的“标准积木”。
  • LinearModelFit：这是核心函数。它运用了最小二乘法（也就是我们在希尔伯特空间中找最近的投影），算出了那组最优系数。
  • 结果验证：运行代码后，请检查输出的系数。如果一切正常，您应该能看到离焦项接近 1.5，散光项接近 0.5，彗差项接近 0.3。哪怕数据里混入了噪声，Zernike 分析也能把真实的病灶“抓”出来。

5. Dr. X 的备忘录

  1. 视角转换：以前您看角膜是看“曲率半径”，现在看角膜要看“Zernike 频谱”。
  2. 正交的意义：正交性保证了我们在矫正一种像差时，不会意外引入另一种像差。这是个性化手术（如 Wavefront-guided LASIK）安全性的数学基石。
  3. 工具的力量：您不需要背诵 Zernike 多项式的公式。您只需要知道它是描述波前的字母表，而 Wolfram 是帮您拼写的打字机。

下周预告：

既然我们已经能用 Zernike 积木描述任意复杂的静态角膜，那么如果角膜不仅是不规则的，而且光线经过它之后发生了“质变”（比如变得模糊、发生散射）怎么办？下周，我们将进入第 5 章：算子理论与特征值——用矩阵的语言来解构模糊的图像。