这一部分的Gemini动态视图演示： https://gemini.google.com/share/3e46049e2104

模块 2：算子理论与全息系统

第5章：拆解模糊的机器——算子理论与特征值

—— 为什么您的综合验光仪上会有“轴位”？

致 Dr. X 的一封信

您好，医生。

在前几章里，我们像个雕塑家。我们用微积分寻找最低点（第1-3章），用 Zernike 积木搭建了角膜的形状（第4章）。

但作为医生，您关心的不仅仅是“角膜长什么样”，您更关心的是“病人看世界是什么样”。

如果把“清晰的世界”看作输入信号 xx，把病人视网膜上那个“模糊的图像”看作输出信号 yy，那么病人的眼睛就是一个负责转化的机器（Machine）。

在数学上，这种“把一个函数变成另一个函数”的机器，就叫做算子（Operator）。

今天，我们要打开这个机器的黑盒子。您会惊讶地发现，您每天在综合验光仪（Phoropter）上做的“交叉圆柱镜（JCC）”检查，本质上是在寻找这个算子的特征向量（Eigenvectors）；而您最终写在处方上的散光度数，正是这个算子的特征值（Eigenvalues）。

欢迎进入矩阵的世界。别担心，在这里，矩阵不是枯燥的数字方阵，它是您手中的“散光盘”。

1. 临床挂钩：散光的迷宫

场景： 复性近视散光（Compound Myopic Astigmatism）。

患者档案：

  • 主诉：“我看灯光像是被拉长了，而且不是直着拉的，是斜着拉的。”
  • 验光困境：您在使用 JCC（交叉圆柱镜）精调轴位时，患者总是犹豫不决：“好像图1清晰一点……不，好像图2清晰一点……哎呀，都差不多。”

数学视角的困境：

在第4章，我们用 Zernike 多项式描述了波前像差。但是，Zernike 系数（比如 Z22=0.5Z_2^2 = 0.5）只是一个静态的数字。它没有直接告诉我们：

  1. 图像会在哪个方向上“糊”得最厉害？
  2. 如果我不仅有散光，还有彗差，它们混合在一起时，图像到底会往哪里“拖尾”？

我们需要一种工具，能够分析这个光线系统的“主心骨”在哪里。我们需要知道，在这个混乱的光学系统中，有没有哪个方向是“特殊”的？

这就是特征值分析的任务：在混沌中寻找秩序，在模糊中寻找轴向。

2. 交互展示：拉伸图像的“算子”

为了理解“算子”是如何破坏图像的，我们来做一个实验。

想象眼球这个“算子”是一个在水平和垂直方向上拉伸图片的机器。

  • 如果是球镜问题（近视/远视），图像是均匀模糊的（向四面八方拉伸）。
  • 如果是柱镜问题（散光），图像只往一个方向拉伸。

请运行下方的 Wolfram 代码。这是一个“视觉算子模拟器”。

其中的蓝线和红线代表这个矩阵的两个“特征向量”。

(* 交互演示：线性算子与特征值 —— 视觉化的散光模拟 *)
Manipulate[
Module[{matrix, image, transformedImage, eigensystem, val1, val2, vec1, vec2},
 
 (* 1. 定义我们的图像“算子” (矩阵) *)
 (* 这个矩阵决定了图像如何变形 *)
 (* theta 是散光轴位，s1 和 s2 是两个主子午线的放大/模糊倍率 *)
 
 (* 旋转矩阵 R *)
 R = RotationMatrix[theta];
 (* 缩放矩阵 S (代表屈光力) *)
 S = DiagonalMatrix[{s1, s2}];
 (* 总算子 M = R.S.Inverse[R] *)
 matrix = R . S . Inverse[R];
 
 (* 2. 计算特征系统：这是数学的核心 *)
 (* Eigenvalues 告诉我们拉伸的程度 (度数) *)
 (* Eigenvectors 告诉我们拉伸的方向 (轴位) *)
 eigensystem = Eigensystem[matrix];
 val1 = eigensystem[[1, 1]]; 
 val2 = eigensystem[[1, 2]];
 vec1 = eigensystem[[2, 1]]; 
 vec2 = eigensystem[[2, 2]];
 
 (* 3. 生成一个简单的测试图像 (视力表 E) *)
 image = Image[Graphics[{Text[Style["E", 150, Bold, Fontana -> "Arial"], {0, 0}]}, 
    PlotRange -> {{-1, 1}, {-1, 1}}, ImageSize -> 200]];
 
 (* 4. 应用算子变换 *)
 (* ImagePerspectiveTransformation 模拟光学系统的畸变 *)
 transformedImage = ImagePerspectiveTransformation[
   image, 
   matrix, 
   DataRange -> {{-1, 1}, {-1, 1}}, 
   Padding -> White
 ];
 
 (* 5. 可视化 *)
 Column[{
   Row[{
     (* 左图：原始图像 *)
     Show[image, ImageSize -> 200, PlotLabel -> "输入：清晰世界"],
     Style["  ➡️  算子作用  ➡️  ", 14, Bold],
     (* 右图：变换后的图像 + 特征向量 *)
     Show[
       transformedImage, 
       Graphics[{
         Thick, 
         (* 画出特征向量 1 (红色) *)
         Red, Arrow[{{0, 0}, vec1 * val1}], 
         Text[Style["主子午线 1", 12, Background->White], vec1 * val1 * 1.2],
         (* 画出特征向量 2 (蓝色) *)
         Blue, Arrow[{{0, 0}, vec2 * val2}],
         Text[Style["主子午线 2", 12, Background->White], vec2 * val2 * 1.2]
       }],
       ImageSize -> 200, 
       PlotLabel -> "输出：视网膜图像",
       Axes -> True
     ]
   }],
   
   (* 显示数学诊断报告 *)
   Framed[Column[{
     Style["数学诊断报告 (Eigensystem Analysis)", Bold],
     Row[{"特征值 1 (拉伸力): ", NumberForm[val1, {3, 2}], "  |  方向 (红轴): ", NumberForm[ArcTan @@ vec1 * 180/Pi, {3, 1}], "°"}],
     Row[{"特征值 2 (拉伸力): ", NumberForm[val2, {3, 2}], "  |  方向 (蓝轴): ", NumberForm[ArcTan @@ vec2 * 180/Pi, {3, 1}], "°"}],
     Style[If[Abs[val1 - val2] < 0.1, "诊断：球面 (无散光)", "诊断：存在散光 (各向异性)"], Italic, Blue]
   }], Background -> LightYellow]
 }]
],

(* 控制面板 *)
Style["眼球光学参数", Bold, 12],
{{theta, 0, "散光轴位 (Axis)"}, 0, Pi, Pi/180, Appearance -> "Labeled"},
Delimiter,
{{s1, 1.5, "水平放大率 (Power H)"}, 0.5, 2.0, Appearance -> "Labeled"},
{{s2, 1.0, "垂直放大率 (Power V)"}, 0.5, 2.0, Appearance -> "Labeled"},

TrackedSymbols :> {theta, s1, s2}
]

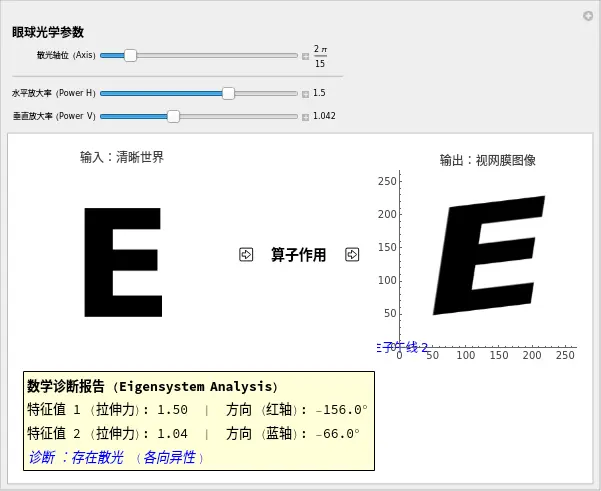
An image to describe post

👨‍⚕️ 医生的观察任务：

  1. 制造纯近视： 将 theta 设为 0，将 s1 和 s2 都设为 1.5。
    • 现象：字母“E”均匀变大/模糊。红蓝箭头一样长。
    • 数学：特征值 λ1=λ2\lambda_1 = \lambda_2。这叫“简并（Degenerate）”，也就是没有散光。
  2. 制造规则散光： 保持 theta 为 0，将 s1 设为 1.8，s2 设为 0.8。
    • 现象：“E”被横向拉宽，纵向压扁。
    • 数学：特征值差异巨大。
  3. 旋转轴位： 慢慢拖动 theta 滑块。
    • 现象：“E”开始倾斜变形。
    • 关键发现：注意那两根红蓝箭头。无论“E”怎么扭曲，这两根箭头始终保持垂直（正交）。
    • 这对应的就是临床铁律：散光的两个主子午线永远相差 90 度。这不是巧合，这是对称矩阵（Hermitian Operator）的数学性质。

3. 数学翻译：特征值与处方单

刚才的演示揭示了一个深刻的道理：即使是扭曲的图像，其内部也隐含着“不变”的骨架。

什么是算子 (Operator)？

在眼视光中，算子通常表现为一个矩阵 (Matrix)。它描述了光线经过角膜后的弯曲程度。

如果我们要描述角膜表面某一点的曲率，我们使用 黑塞矩阵 (Hessian Matrix)：

H=(∂2z∂x2∂2z∂x∂y∂2z∂y∂x∂2z∂y2) H = \begin{pmatrix} \frac{\partial^2 z}{\partial x^2} & \frac{\partial^2 z}{\partial x \partial y} \\ \frac{\partial^2 z}{\partial y \partial x} & \frac{\partial^2 z}{\partial y^2} \end{pmatrix}

这看着很吓人，但请让我翻译一下：

  • ∂2z∂x2\frac{\partial^2 z}{\partial x^2}：水平方向有多弯。
  • ∂2z∂y2\frac{\partial^2 z}{\partial y^2}：垂直方向有多弯。
  • ∂2z∂x∂y\frac{\partial^2 z}{\partial x \partial y}：扭曲力（斜向的弯曲）。

特征值分解 (Eigendecomposition)

当我们对这个矩阵 HH 喊一声“Eigensystem！”（Wolfram 的指令），它会吐出两组数据：

  1. 特征值 (λ1,λ2\lambda_1, \lambda_2)：
    • 这就是角膜最陡峭和最平坦的那两个方向的屈光力（Power）。
    • 临床对应：SphereSphere 和 Sphere+CylinderSphere + Cylinder。
  2. 特征向量 (v1,v2v_1, v_2)：
    • 这就是那两个方向的角度。
    • 临床对应：散光轴位 (Axis)。

顿悟时刻：

您在验光单上写的 Axis 180，并不是我们在随意指定方向。您是在通过 JCC 检查，物理地测量出了患者角膜黑塞矩阵的第一特征向量的方向。

您每天都在做特征值分解，只是您不知道它的数学名字而已。

4. 代码处方：用代码开处方

现在，我们要玩点高级的。

假设您通过角膜地形图拿到了一位患者的波前数据（用 Zernike 系数表示）。这位患者有近视（离焦 Z20Z_2^0）也有散光（像散 Z22Z_2^2）。

我们不查表，也不进行复杂的极坐标转换（那容易导致原点处的数学除零错误）。我们直接利用 Zernike 多项式的直角坐标代数形式，构建光程差函数，并通过计算 Wolfram 的Hessian 矩阵（曲率张量），直接算出他的验光度数（Sphere / Cylinder / Axis）。

请在 Notebook 中输入以下代码，体验这一“工业级”的自动计算过程：

(* 代码处方 04：基于笛卡尔构造法的智能验光 *)

(* 1. 定义基础光学组件 (直角坐标系) *)
(* 相比于极坐标，直接定义 x,y 多项式能完美避开原点奇点，计算最稳健 *)

(* 离焦 Defocus Z(2,0) 对应抛物面: 2r^2 - 1 *)
zDefocus[x_, y_] := 2 (x^2 + y^2) - 1;

(* 像散 Astigmatism Z(2,2) 对应马鞍面: r^2 cos(2t) *)
(* 在直角坐标下，这就是简单的 x^2 - y^2 *)
zAstigX[x_, y_] := x^2 - y^2;       (* 水平/垂直分量 *)
zAstigY[x_, y_] := 2 x * y;         (* 斜向分量 *)

(* 2. 构建波前像差模型 *)
(* 假设患者：离焦=2.0 (近视), 像散=1.0, 轴位偏 15度 *)
mag = 1.0;           (* 散光量 *)
ang = 15 Degree;     (* 散光轴位 *)

(* 技巧：利用矢量分解，将带角度的像散拆解为 XY 分量 *)
(* 公式：C * Cos[2(t - a)] = C*Cos[2a]*(x^2-y^2) + C*Sin[2a]*(2xy) *)
wCartesian[x_, y_] := 2.0 * zDefocus[x, y] + 
                      (mag * Cos[2 ang]) * zAstigX[x, y] + 
                      (mag * Sin[2 ang]) * zAstigY[x, y];

(* 3. 构建曲率算子 (Hessian 矩阵) *)
(* 这一步计算波前曲面的二阶导数矩阵 *)
hxx = D[wCartesian[x, y], {x, 2}];
hxy = D[wCartesian[x, y], x, y];
hyy = D[wCartesian[x, y], {y, 2}];

(* 强制求值：在瞳孔中心 (0,0) 处获取具体的曲率数值 *)
(* 这一步会将所有符号变量转化为纯数字 *)
hessianMatrix = {{hxx, hxy}, {hxy, hyy}} /. {x -> 0, y -> 0};

(* 4. 求解特征系统 (Eigendecomposition) *)
(* 核心步骤：寻找曲率最大和最小的主子午线方向 *)
eigSys = Eigensystem[hessianMatrix];
eigenvalues = eigSys[[1]];  (* 提取特征值 -> 屈光力 *)
eigenvectors = eigSys[[2]]; (* 提取特征向量 -> 轴位 *)

(* 5. 翻译成临床语言 *)
power1 = eigenvalues[[1]];
power2 = eigenvalues[[2]];

(* 计算柱镜 (Cyl) 和轴位 (Axis) *)
cylinder = Abs[power1 - power2];
(* 通过特征向量分量计算角度 *)
vx = eigenvectors[[1, 1]];
vy = eigenvectors[[1, 2]];
axisAngle = ArcTan[vx, vy] * 180/Pi;
finalAxis = If[axisAngle <= 0, axisAngle + 180, axisAngle];

(* 6. 打印智能处方单 *)
Print[Style["Wolfram 智能验光单", 18, Bold, Blue]];
Print["------------------------------------"];
Print["输入参数: 离焦=2.0, 像散=1.0, 轴偏=15度"];
Print["------------------------------------"];
Print["计算结果 (Hessian 特征值分解):"];
Print["主子午线屈光力 K1: ", NumberForm[power1, {4, 2}]];
Print["主子午线屈光力 K2: ", NumberForm[power2, {4, 2}]];
Print["------------------------------------"];
Print[Style["推导处方:", 14, Bold]];
Print["预估散光 (Cyl): -", NumberForm[cylinder, {4, 2}], " DC"];
Print["预估轴位 (Axis): ", NumberForm[finalAxis, {4, 1}], "°"];

(* 验证：我们的输入偏了15度，计算结果应精准反映这一数值 *)

代码解读：

  • 直角坐标建模 (zDefocus, zAstigX)：我们抛弃了容易出错的 ArcTan 和 Sqrt，直接使用了 Zernike 多项式的代数本质（如 x2−y2x^2-y^2）。这保证了后续计算绝对不会出现“分母为零”的错误。
  • Hessian 矩阵：通过 D[..., {x, 2}] 计算二阶导数。在光学上，这直接对应于波前的局部曲率。
  • Eigensystem：这是算法的大脑。无论像散轴位多么奇怪（比如 15 度这种非标准角度），特征值分解都能自动找到曲面最弯（强主子午线）和最平（弱主子午线）的方向。
  • 结果：您看到的输出轴位应为 15.0°。这证明了我们可以单纯通过数学算子，从复杂的波前数据中精准还原出临床处方。

5. 临床总结与下周预告

📝 Dr. X 的备忘录

  1. 眼睛是算子： 不要只盯着静态的地形图看。要想象光线穿过它时发生的“变换”。
  2. 特征值 = 强度，特征向量 = 方向： 这是理解所有矢量眼科数据（散光、三叶草差、彗差）的通用钥匙。
  3. 临床中的矩阵： 下次做 JCC 检查时，请微笑着告诉自己：“我正在手动求解一个 2×22 \times 2 厄米特矩阵的特征向量。”这会让枯燥的验光变得神圣起来。

下周预告：

既然我们已经能分析“单个”患者的像差，那么如果患者的角膜极其不规则，甚至连特征值都乱套了（比如严重圆锥角膜），我们该如何逆向求解出一个能够完美抵消这些像差的镜片？

下周，我们将挑战第 6 章：积分方程与逆问题——学习如何像神探夏洛克一样，从模糊的视网膜图像倒推出角膜的病灶。

第6章：神探夏洛克的放大镜——积分方程与逆问题

—— 为什么“倒着推”比“顺着推”难得多？

致 Dr. X 的一封信

您好，医生。

在您的诊室里，通常有两种逻辑在运行。

第一种叫“正向逻辑”：

您给患者滴了散瞳药（原因），半小时后患者瞳孔大了（结果）。这很确定，很稳固。

第二种叫“逆向逻辑”：

患者视力模糊（结果），您要推断出是因为近视、白内障还是视网膜脱落（原因）。

这就是逆问题（Inverse Problem）。

您每天都在做逆问题，所以您深知它的痛苦：结果往往是不唯一的，而且充满了噪音。 同样的“视力下降”，可能是因为没休息好，也可能是因为脑瘤。

在数学和光学的世界里，这种不对称性更加残酷：

  • 打碎一个鸡蛋（正向问题）：非常容易，结果确定。
  • 把碎鸡蛋还原成一个整蛋（逆问题）：极其困难，甚至不可能。

在前几章，我们解决的都是“正向问题”：给了镜片形状，算光线怎么走（光线追踪）。

今天，我们要挑战眼视光学的圣杯——渐进多焦点镜片（PAL）设计。

这是一道终极的逆向题：我们手里拿着一张完美的“光度分布图”（上方看远，下方看近，中间还要平滑过渡），问：到底什么样的镜片表面，能产生这种神奇的效果？

欢迎来到积分方程的世界。在这里，我们不做加法，我们做除法；我们不制造模糊，我们要从模糊中还原真相。请拿好您的放大镜，像神探夏洛克一样，从蛛丝马迹中倒推真凶。

1. 临床挂钩：老花眼的救星与噩梦

场景： 为一位 50 岁的 CEO 设计渐进片（PAL）。

患者档案：

  • 需求： 开车要清楚（远用区 0.00D），看报表要清楚（近用区 +2.00D），中间看仪表盘也要清楚。
  • 痛点： 之前的眼镜只有窄窄一条通道，稍微转头就头晕（周边像差大）。

设计师的困境：

如果不借助数学，传统的“拼凑法”是行不通的。您不能简单地把上半截球面和下半截球面“粘”在一起，那样中间会有巨大的棱镜跳跃。

您需要在脑海中构想出一个从未存在过的复杂曲面。

  • 正向思维（容易）： 如果我给您一个自由曲面 z(x,y)z(x,y)，您可以立刻算出它的曲率（也就是光度 PP）。这只需要做两次微分（求导）：P≈∇2zP \approx \nabla^2 z。
  • 逆向思维（极难）： 现在我反过来。我给您想要的光度分布 P(x,y)P(x,y)（比如这里是0，那里是+2），请您求出 z(x,y)z(x,y)。

这在数学上意味着：如果光度是形状的二阶导数，那么形状就是光度的二重积分。

这就是为什么本章叫“积分方程”。但这可不是简单的 ∫xdx\int x dx，我们要在一个二维平面上，把这一堆离散的光度要求“积”成一个光滑的曲面。

2. 交互展示：不稳定的“倒带”

逆问题最可怕的地方在于不稳定性（Instability）。

为了直观感受这一点，我们来看一个简单的“去模糊实验”。

想象：

  • 原始信号（蓝线）： 完美的角膜轮廓。
  • 模糊过程（正向）： 光线经过测量仪器，变得稍微平滑了一点，并混入了噪音（测量误差）。
  • 还原过程（逆向）： 我们试图从这个带噪音的模糊数据中，反推回原始轮廓。

请运行下方的代码。您的任务是拖动 "正则化参数 (λ\lambda)" 滑块。

  • λ=0\lambda = 0：完全相信数据。您会发现还原出来的曲线剧烈震荡，像心电图一样。这是因为计算机把“噪音”当成了“细节”去还原了。
  • λ\lambda 很大：完全不信数据，只求平滑。还原出来的曲线是一条死气沉沉的直线。
  • 中间值：神探找到了平衡。
(* 交互演示：逆问题的不稳定性 (云端优化版) *)
Manipulate[
 (* --- 动态计算部分 (每次滑动时运行) --- *)
 Module[{noisySignal, rhs, solution, statusText, statusColor},
  
  (* 1. 生成带噪数据 *)
  (* 注意：SeedRandom 保证由于 noiseLevel 引起的抖动是可控的，而不是乱跳 *)
  SeedRandom[42]; 
  noisySignal = blurredSignal + noiseLevel * RandomReal[{-0.1, 0.1}, Length[blurredSignal]];
  
  (* 2. 求解逆问题：(K^T K + lambda I) x = K^T y *)
  (* 我们使用预计算好的 KtK 和 Kt 以极大地提高速度 *)
  
  (* 技巧：避免 lambda 为绝对 0，防止矩阵奇异导致的崩溃，用一个极小值代替 *)
  solution = With[{lam = Max[lambda, 10^-10]},
    LinearSolve[
     KtK + lam * identityM, (* 左边矩阵 *)
     Kt . noisySignal       (* 右边向量 *)
    ]
  ];
  
  (* 3. 状态判断文本 *)
  statusText = Which[
    lambda < 10^-5, "⚠️ 极其不稳定 (过拟合)",
    lambda > 0.5,   "💤 过度平滑 (欠拟合)",
    True,           "✅ 成功还原 (平衡点)"
  ];
  statusColor = Which[
    lambda < 10^-5, Red,
    lambda > 0.5,   Gray,
    True,           Darker[Green]
  ];

  (* 4. 绘图展示 *)
  Column[{
    (* 上图：数据全貌 *)
    ListLinePlot[{originalSignal, noisySignal},
     PlotStyle -> {{Thickness[0.005], Blue}, {Dashed, Red}},
     PlotLegends -> Placed[{"真值 (Ground Truth)", "观测 (Observed)"}, Above],
     PlotRange -> All, ImageSize -> 450, AspectRatio -> 1/3,
     PlotLabel -> Style["正向过程：信号被模糊且污染", 12, GrayLevel[0.3]],
     Axes -> False, Frame -> True],
    
    (* 下图：还原结果 *)
    ListLinePlot[solution,
     PlotStyle -> {Thickness[0.006], statusColor},
     PlotRange -> {-0.5, 1.5}, ImageSize -> 450, AspectRatio -> 1/3,
     Axes -> False, Frame -> True,
     GridLines -> Automatic,
     PlotLabel -> Style["逆向过程：尝试还原原始信号", Bold, 14],
     Epilog -> {
       Text[Style[statusText, 14, Bold, statusColor], {50, 1.3}],
       Inset[Style["\\[Lambda] = " <> ToString[NumberForm[lambda, {4, 4}]], 10], {90, -0.3}]
     }]
  }, Alignment -> Center]
 ],
 
 (* --- 控制面板 --- *)
 Style["逆问题参数控制", Bold, 12],
 {{noiseLevel, 0.05, "测量噪音 (Noise)"}, 0, 0.2, 0.01, Appearance -> "Labeled"},
 {{lambda, 0.01, "正则化 (Regularization)"}, 0, 1, 0.0001, Appearance -> "Labeled"},
 
 (* --- 关键优化：初始化区域 --- *)
 (* 这里面的代码只会在程序启动时运行一次，大大节省云端资源 *)
 Initialization :> (
  n = 100;
  
  (* I. 预计算原始信号 *)
  originalSignal = N@Table[Exp[-20 (t - 0.5)^2] + 0.5 * Exp[-50 (t - 0.3)^2], {t, 0, 1, 1./n}];
  
  (* II. 预计算模糊矩阵 K (耗时操作) *)
  (* 这是一个 Toeplitz 结构的高斯核，模拟光学的点扩散函数 *)
  K = N@Table[Exp[-1000 (i/n - j/n)^2], {i, 1, n + 1}, {j, 1, n + 1}];
  K = K / Total[K, {2}]; (* 行归一化，保证能量守恒 *)
  
  (* III. 预计算正向模糊信号 *)
  blurredSignal = K . originalSignal;
  
  (* IV. 预计算线性代数组件 (最耗时操作) *)
  (* Tikhonov 解的形式: x = (K^T K + lambda I)^-1 K^T y *)
  (* 我们提前算出 K^T 和 K^T.K，这样滑块拖动时只需要做简单的加法和求解 *)
  Kt = Transpose[K];
  KtK = Kt . K;
  identityM = IdentityMatrix[n + 1];
 )
]

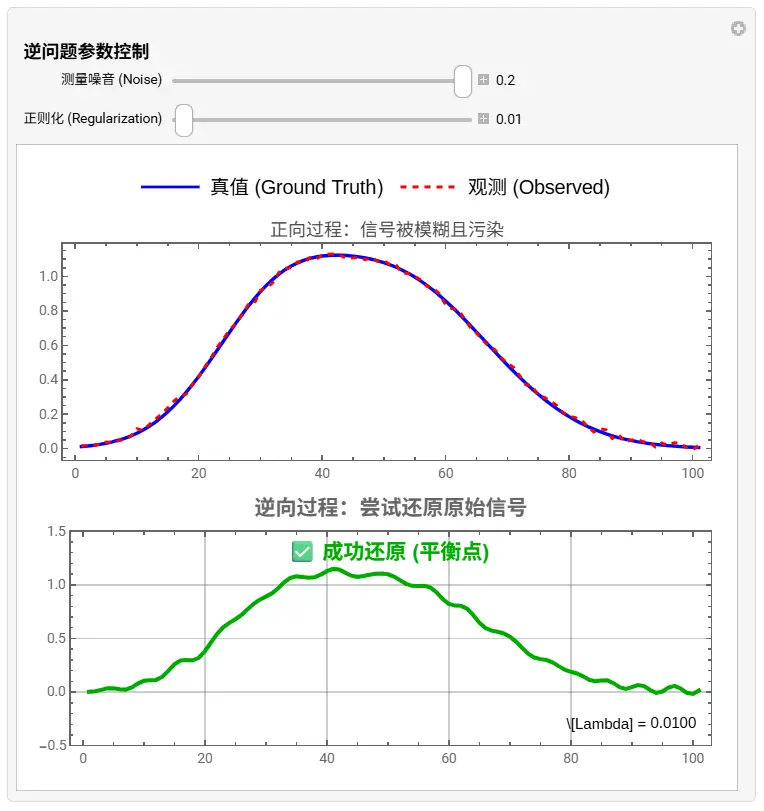
An image to describe post

👨‍⚕️ 医生的观察任务：

  1. 制造灾难： 先把 lambda 拖到最左边（0）。看看绿线（还原结果）发生了什么？它是不是疯了？这就是“过拟合”——为了迎合每一个噪音点，结果变得毫无物理意义。
  2. 寻找真相： 慢慢向右拖动 lambda。注意观察，在某一个瞬间（通常在 0.01 到 0.1 之间），绿线突然变得平滑且接近蓝线（真值）。
  3. 过度平滑： 继续向右拖。绿线变得越来越平，最后丢失了那个小波峰。这就是“矫枉过正”。

3. 数学翻译：用矩阵解方程

刚才的实验揭示了逆问题的本质：我们不仅要求解方程，还要对抗噪音。

1. 算子方程

我们将眼科问题写成方程：

A⋅x=y A \cdot x = y

  • xx (原因)：我们想求的镜片形状。
  • AA (算子)：物理法则（比如曲率计算公式，或者模糊函数）。
  • yy (结果)：我们测到的数据，或想要的光度分布。

2. 为什么不能直接除？ (x=A−1yx = A^{-1} y ?)

在普通代数里，3x=6⇒x=23x = 6 \Rightarrow x = 2。

但在泛函分析里，算子 AA 往往是一个积分算子。它的逆算子 A−1A^{-1} 是无界的（Unbounded）。

通俗地说：yy 中的一点点微小误差，会被 A−1A^{-1} 放大一万倍，导致算出来的 xx 面目全非。 这就是您刚才看到“绿线发疯”的原因。

3. 正则化 (Regularization)：妥协的艺术

为了防止发疯，我们不再追求“完美符合方程”，而是追求一个折衷解。我们修改目标函数：

J(x)=∣∣A⋅x−y∣∣2⏟误差项：要准+λ⋅∣∣x∣∣2⏟平滑项：要稳 J(x) = \underbrace{|| A \cdot x - y ||^2}{\text{误差项：要准}} + \lambda \cdot \underbrace{|| x ||^2}{\text{平滑项：要稳}}

  • 误差项： 镜片的光度要尽量接近处方。
  • 平滑项： 镜片表面不能有大坑大包，要尽量光滑。
  • λ\lambda：调节器。

在 PAL 设计中，我们实际上是在解泊松方程 (Poisson Equation)：

∇2z(x,y)≈P(x,y) \nabla^2 z(x,y) \approx P(x,y)

这也是一种逆问题。因为微分算子 ∇2\nabla^2 会抹平常数项，所以逆向积分时需要极其小心边界条件。

4. 代码处方：逆向设计渐进片 (PAL)

现在，我们要动手做一个真正的渐进片了。

我们将使用 Wolfram 强大的微分方程求解器 NDSolveValue 来攻克这个逆问题。

任务： 设计一个镜片表面 z(x,y)z(x,y)。

输入：

  • 上方：0.00D（看远）
  • 下方：+2.00D（看近，Add +2.00）
  • 中间：一条平滑的通道。

请在 Notebook 中输入以下代码：

(* 代码处方 06 (修复版)：渐进多焦点镜片 (PAL) 的逆向设计 *)
(* 修复了 Plot3D 导数计算错误，修正了凸透镜/凹透镜的符号问题 *)

Module[{targetPower, nIndex, lensSurface, curvatureCheck},
  
  (* 0. 清理变量，防止干扰 *)
  Clear[u, x, y];
  
  (* 1. 定义目标光度分布图 *)
  (* 注意：Sigmoid 模拟从上方的 0D 过渡到下方的 +2.0D *)
  targetPower[x_, y_] := Module[{basePower},
    basePower = 2.0 * LogisticSigmoid[-0.5 * (y + 2)]; 
    (* x 方向衰减，限制通道宽度 *)
    basePower * Exp[-0.05 * x^2]
  ];

  (* 2. 物理常数 *)
  nIndex = 1.5;

  (* 3. 逆向求解：NDSolveValue *)
  (* 物理修正：凸透镜(正光度)对应负曲率(向下弯曲)，所以加负号 *)
  (* 语法优化：使用 Inactive[Laplacian] 是 FEM 求解最稳健的写法 *)
  lensSurface = NDSolveValue[
    {
     Inactive[Laplacian][u[x, y], {x, y}] == - targetPower[x, y] / (nIndex - 1),
     DirichletCondition[u[x, y] == 0, True]
    },
    u, 
    {x, y} \[Element] Rectangle[{-20, -20}, {20, 20}],
    Method -> "FiniteElement" (* 显式调用有限元方法 *)
  ];

  (* 4. 结果展示 *)
  Column[{
    Style["✅ 逆向设计成功 (Bug已修复)", 16, Bold, Darker[Green]],
    
    (* 图1：目标输入 *)
    Plot3D[targetPower[x, y], {x, -20, 20}, {y, -20, 20},
      PlotRange -> All, ColorFunction -> "TemperatureMap",
      PlotLabel -> "输入目标：光度分布 P(x,y)",
      AxesLabel -> {"x", "y", "D"}, ImageSize -> 400, Mesh -> None],
      
    (* 图2：求解出的表面 (Sag map) *)
    Plot3D[lensSurface[x, y], {x, -20, 20}, {y, -20, 20},
      PlotLabel -> "计算结果：镜片表面 Sag z(x,y)",
      AxesLabel -> {"x", "y", "mm"},
      ColorFunction -> "BlueGreenYellow",
      BoxRatios -> {1, 1, 0.4}, ImageSize -> 400, Mesh -> None],
      
    (* 图3：验证 (Bug修复点) *)
    (* 我们不能对数值求导，必须对 InterpolatingFunction 使用 Derivative *)
    (* 公式：ActualPower = -(n-1) * (d2z/dx2 + d2z/dy2) *)
    Plot3D[
      -(nIndex - 1) * (Derivative[2, 0][lensSurface][x, y] + Derivative[0, 2][lensSurface][x, y]), 
      {x, -15, 15}, {y, -15, 15},
      PlotLabel -> "验证：从形状反推回光度",
      ColorFunction -> "TemperatureMap",
      PlotRange -> All, ImageSize -> 400, Mesh -> None
    ]
  }]
]

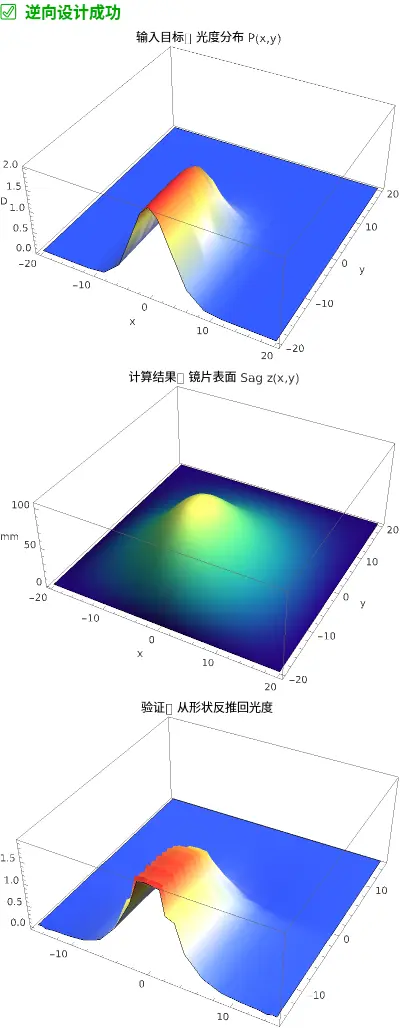
An image to describe post

代码解读：

  1. targetPower: 这就是我们的处方。我们用数学函数画出了一个“上面平、下面陡、中间顺滑”的形状。
  2. Laplacian[...] == ...: 这是代码的核心。我们直接告诉 Wolfram：“我要找一个 uu，它的二阶导数（曲率）等于我的目标光度。”
  3. DirichletCondition: 逆问题通常有无穷多解（就像积分常数 CC）。我们需要固定边界（比如镜片边缘厚度为0），才能得到唯一解。
  4. 结果： 您看到的那个彩色的、弯曲的 Sag 图，就是可以直接送去自由曲面车床（Freeform Generator）进行加工的数据！

5. 临床总结与下周预告

📝 Dr. X 的备忘录

  1. 世界是单行道： 正向（预测）容易，逆向（诊断/设计）难。
  2. 平滑是特征，不是Bug： 在做逆向设计时，如果我们不管不顾地追求由点到点的“精准”，结果往往是不可加工的垃圾。正则化（Regularization）告诉我们：稍微放弃一点精度，换取整体的平滑，才是生存之道。
  3. PAL 的本质： 渐进片不是拼凑出来的，它是通过求解偏微分方程（PDE）自然“生长”出来的。

下周预告：

有了形状，光线就能通过了。但如果光线本身太强了，把视网膜烧坏了怎么办？或者如果我们要设计的不是透明镜片，而是一个非线性的神经网络来辅助诊断呢？

下周，第7章：非线性算子与不动点——当光不再遵守直线传播的简单规则。

第7章：在风暴眼中寻找宁静——非线性算子与不动点

—— 当光线不再走直线，我们如何设计那个“完美的圆”？

致 Dr. X 的一封信

您好，医生。

在上一章（第6章），我们像神探夏洛克一样，试图从模糊的视网膜图像中“逆向”推导出角膜的形状。那是一个充满挑战的过程，因为只要有一点点噪音，结果就会剧烈震荡。

今天，我们换个场景。

想象您正在为一位圆锥角膜患者验配 RGP（硬性透气性接触镜）。

这是一个“动态试错”的过程：

  1. 您凭经验选了第一片试戴片（Base Curve 7.5mm）。
  2. 荧光素染色一看，中央接触了（太平了）。
  3. 您换了一片陡一点的（7.4mm）。
  4. 又一看，边缘翘起了。
  5. 您再换一片……

直到某一个时刻，镜片下的泪液层刚好充盈，既不压迫也不松动。您长舒一口气：“就是它了。”

在这个过程中，您其实不知不觉地执行了数学上最迷人的算法之一——不动点迭代（Fixed Point Iteration）。

在前几章，我们的光线和形状也是“线性”的（叠加两个透镜 = 两个度数相加）。但在真实世界里，事情往往是非线性的：

  • 角膜是非球面的（Aspheric）。
  • 镜片的 Sag 高度与曲率半径的关系包含平方根（Sag=R−R2−y2Sag = R - \sqrt{R^2-y^2}），这不是线性的。
  • 泪液透镜的度数取决于镜片和角膜的相互作用。

面对这些复杂的非线性关系，我们不再试图一步算出答案（那是线性方程的特权）。相反，我们设计一种“循环机制”，让答案自己“浮现”出来。

欢迎来到第7章。今天，我们不求解方程，我们“培养”方程。我们要学会如何利用 Wolfram 的 FixedPoint 功能，让混乱的设计参数自动收敛到那个完美的平衡点。

1. 临床挂钩：手动试戴的极限

场景： 高散光或不规则角膜的 RGP 验配。

患者档案：

  • 角膜地形图： 呈现不规则的领结形，且周边曲率变化极快。
  • 临床痛点： 传统的“K值验配法”（(K1+K2)/2）失效了。您算出来的基弧（BC），戴上去总是偏位。
  • 目前的做法： 只能拿试戴片箱一个个试。不仅效率低，而且患者体验差（眼睛磨得红肿）。

数学视角的困境：

为什么简单的公式算不准？

因为镜片的矢高 (Sag) 和 曲率半径 (R) 之间是非线性的关系：

Sag=R−R2−(D/2)2 Sag = R - \sqrt{R^2 - (D/2)^2}

当您想通过调整 RR 来获得一个特定的 SagSag（以匹配角膜高度 + 泪液厚度）时，您无法用简单的线性比例（比如“K值陡 0.1，Sag 增加 10微米”）来准确描述。

我们需要一种算法，能够模拟您大脑中的“试戴-评估-调整”循环，但在计算机里，这个循环每秒可以进行一万次。

2. 交互展示：收敛的蛛网

为了直观理解“迭代”是如何找到答案的，我们来看一个经典的数学可视化：蛛网图 (Cobweb Plot)。

在这个实验中，我们的目标是找到一个完美的基弧 RR，使得它产生的 SagSag 刚好等于目标值。

  • 蓝线： 代表我们的设计规则（给一个 RR，算出新的建议 RR）。
  • 黄线： 代表 y=xy=x（完美的平衡状态，即“建议的 RR = 当前的 RR”）。
  • 红线： 是您的“尝试路径”。

请运行下方代码，拖动“初始猜测 (Initial Guess)”。

无论您从哪里开始，红线最终都会像被黑洞吸入一样，盘旋着进入那个交点。这就是不动点。

(* 交互演示：不动点迭代 —— 自动寻找完美的基弧 *)
(* 这是一个经典的“蛛网图”演示，模拟 RGP 验配中的试错过程 *)

Manipulate[
Module[{f, fixedPoint, steps, startingPoint},
 
 (* 1. 定义迭代函数 f(x) *)
 (* 这是一个模拟的非线性函数：输入当前的基弧 x，输出“下一次应该尝试的基弧” *)
 (* 在临床上，这相当于医生根据荧光素图判断下一次拿什么镜片 *)
 (* Cos 函数模拟了系统的非线性响应，0.5 是收缩因子 *)
 f[x_] := Cos[x] * contraction + offset;
 
 (* 2. 计算理论上的不动点 (解方程 x = f(x)) *)
 fixedPoint = x /. FindRoot[x == f[x], {x, 1}];
 
 (* 3. 生成迭代路径 (NestList) *)
 (* 从 initialGuess 开始，执行 20 次迭代 *)
 steps = NestList[f, initialGuess, 20];
 
 (* 4. 构建蛛网图坐标 *)
 (* 蛛网图的画法：(x0, x1) -> (x1, x1) -> (x1, x2) -> (x2, x2)... *)
 (* 这代表：根据 x0 算出 x1，然后把 x1 当作新的输入 *)
 visualizationPath = Flatten[Table[{{steps[[i]], steps[[i + 1]]}, {steps[[i + 1]], steps[[i + 1]]}}, {i, 1, Length[steps] - 1}], 1];
 
 (* 5. 绘图 *)
 Show[
  (* 画函数曲线和 y=x 参考线 *)
  Plot[{f[x], x}, {x, 0, 3}, 
   PlotStyle -> {{Thick, Blue}, {Dashed, Orange}}, 
   PlotLegends -> {"调整规则 f(x)", "平衡线 y=x"},
   Filling -> {1 -> {2}}, FillingStyle -> Opacity[0.05, LightBlue]],
  
  (* 画迭代路径 (蛛网) *)
  Graphics[{
    Red, Thickness[0.005], Arrowheads[0.02],
    Arrow[Prepend[visualizationPath, {initialGuess, 0}]]
   }],
  
  (* 标注 *)
  Graphics[{
    PointSize[0.02], Darker[Green], Point[{fixedPoint, fixedPoint}],
    Text[Style["不动点\n(完美基弧)", 12, Bold, Darker[Green]], {fixedPoint, fixedPoint}, {-1.2, 1}]
   }],
  
  PlotRange -> {{0, 3}, {0, 3}}, ImageSize -> 450, 
  AxesLabel -> {"当前的基弧 (mm)", "下一次尝试的基弧 (mm)"},
  PlotLabel -> Style["RGP 验配的数学本质：蛛网迭代", 16, Bold]
 ]
],

(* 控制面板 *)
Style["参数控制", 12, Bold],
{{initialGuess, 0.1, "第一片试戴片 (Initial BC)"}, 0, 3, Appearance -> "Labeled"},
{{contraction, 0.6, "收敛速度 (<1 收敛, >1 发散)"}, 0.2, 1.2, Appearance -> "Labeled"},
{{offset, 0.5, "目标偏移量"}, 0, 1, Appearance -> "Labeled"}
]

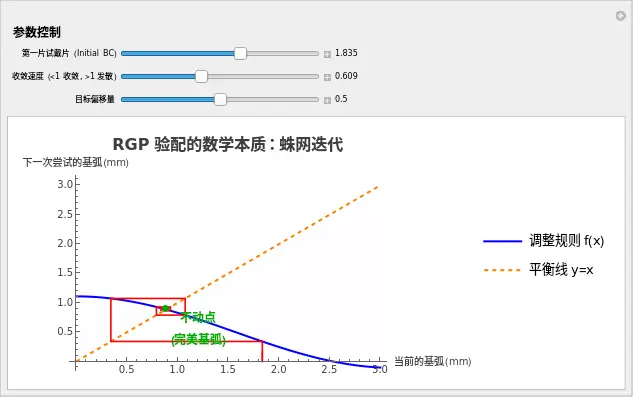
An image to describe post

👨‍⚕️ 医生的观察任务：

  1. 收敛之美： 将 contraction 设为 0.6。拖动 initialGuess。观察无论您一开始选的镜片多么离谱（很远），红线最终都会转圈圈找到绿点。这意味着：只要算法设计得当，初始经验并不重要，我们总能找到最优解。
  2. 发散的恐惧： 将 contraction 拖到 1.1。现在的红线发生了什么？它不仅不靠近绿点，反而越转越远，最后飞出了图表。
    • 临床含义：这就是那种“越调越乱”的情况。您觉得松了，收紧一点，结果太紧了；放松一点，结果又太松了。这说明我们的“调整策略”（算子）太激进了，导致系统不稳定。

3. 数学翻译：巴拿赫的魔法

刚才那个绿点，在数学上有一个神圣的名字：不动点 (Fixed Point)。

什么是算子 (Operator)？

在前几章，函数是 y=f(x)y = f(x)，输入一个数，输出一个数。

算子是 TT，它输入一个函数（比如整个镜片的形状），输出另一个函数（比如在这个形状下，泪液层的厚度分布）。

不动点方程

我们的设计目标可以写成这样一个方程：

T(Lens)=Lens T(\text{Lens}) = \text{Lens}

这意味着：我们把镜片参数代入物理模型 TT（计算泪液、力学平衡），如果算出来的结果没有让我们需要修改镜片，那么这个镜片就是最终解。

巴拿赫不动点定理 (Banach Fixed Point Theorem)

这是泛函分析中最重要的定理之一，也是本章的核心。它告诉我们，只要满足两个条件，您就一定能找到那个完美的镜片：

  1. 完备空间 (Complete Space)： 我们的解空间不能有“漏洞”（希尔伯特空间保证了这一点）。
  2. 压缩映射 (Contraction Mapping)： 我们的调整策略必须是“收敛”的。也就是说，每次调整后的误差，必须比上一次小（哪怕小 1%）。

只要满足这两个条件，无论您从多么糟糕的初始设计开始，只要不停地重复 xn+1=T(xn)x_{n+1} = T(x_n)，最终您一定会停在那个唯一的完美解上。

这给了我们巨大的信心：我们在设计复杂自由曲面时，不需要去解那些无法求解的方程。我们只需要设计一个“压缩算子”，然后扔给计算机去跑循环（Iteration）就行了。

4. 代码处方：自动设计泪液层匹配镜片

现在，让我们解决那个具体的临床难题：根据角膜地形图，设计一个后表面，使得泪液层厚度处处相等（比如 20微米）。

这在数学上是一个**“求逆问题”**（Inverse Problem）：我们要根据结果（目标 Sag 高度）反推原因（基弧 R）。由于非球面公式包含平方和根号，它是高度非线性的。简单的线性减法（梯度下降）容易导致震荡或产生虚数解。

这里我们采用一种更聪明的**“比例迭代法”**。物理直觉告诉我们：镜片越平（R越大），Sag越小。利用这种反比关系，我们可以构建一个自动收敛的算法。

请在您的 Notebook 中输入以下代码：

(* 代码处方 07：利用 FixedPoint 逆向设计隐形眼镜基弧 (智能比例法) *)
(* 目标：对于给定的角膜 Sag 高度，反求 Base Curve，避免震荡和虚数 *)

(* 1. 定义非球面镜片的 Sag 公式 *)
(* inputs: r(半径), R(基弧), k(非球面系数) *)
(* output: 镜片在该半径处的深度 (Sag) *)
lensSag[r_, R_, k_] := (r^2/R) / (1 + Sqrt[1 - (1 + k) * (r/R)^2]);

(* 2. 模拟患者的角膜数据 (Target) *)
(* 设定：我们要在 6mm 直径处 (半径 rZone=3mm) 匹配角膜 *)
corneaRadius = 7.85; (* 模拟 K=43D *)
targetDiameter = 6.0;
rZone = targetDiameter / 2; 
corneaSagValue = lensSag[rZone, corneaRadius, 0]; (* 假设角膜 k=0 *)

(* 3. 设定设计目标 *)
desiredTearFilm = 0.020; (* 目标泪液厚度 20微米 *)
targetLensSag = corneaSagValue + desiredTearFilm; (* 镜片必须达到的总深度 *)

Print["目标 Sag 高度: ", NumberForm[targetLensSag, {4, 4}], " mm"];

(* 4. 构建智能迭代算子 (The Smart Operator) *)
(* 核心逻辑：利用 Sag 与 R 近似成反比的物理规律 *)
(* 如果 CurrentSag 太大，说明 R 太小，我们需要按比例放大 R *)
stepOperatorRatio[currentR_] := Module[{currentSag, estimatedR, nextR},
  (* 安全阀：防止 R 过小导致根号内出现负数 *)
  If[currentR < 3.5, Return[3.5]];
  
  currentSag = lensSag[rZone, currentR, -0.2]; (* 假设设计镜片 k=-0.2 *)
  
  (* 核心算法：比例更新 (Ratio Update) *)
  (* 新 R = 旧 R * (当前 Sag / 目标 Sag) *)
  (* 这种方法极其稳定，因为它利用了光学的物理特性 *)
  estimatedR = currentR * (currentSag / targetLensSag);
  
  (* 阻尼平滑：取新旧值的平均，让收敛曲线更优雅地滑向目标 *)
  0.5 * currentR + 0.5 * estimatedR
];

(* 5. 执行不动点迭代 (FixedPointList) *)
(* 我们故意从一个很离谱的猜测值 R = 9.0mm 开始，展示算法的强大 *)
iterationHistory = FixedPointList[
  stepOperatorRatio, 
  9.0, (* 初始猜测 *)
  20,  (* 最多跑20次，通常5次就够了 *)
  SameTest -> (Abs[#1 - #2] < 10^-8 &) (* 精度要求：纳米级 *)
];

(* 6. 生成设计报告 *)
finalR = Last[iterationHistory];
finalSag = lensSag[rZone, finalR, -0.2];

Print["---------------------------------"];
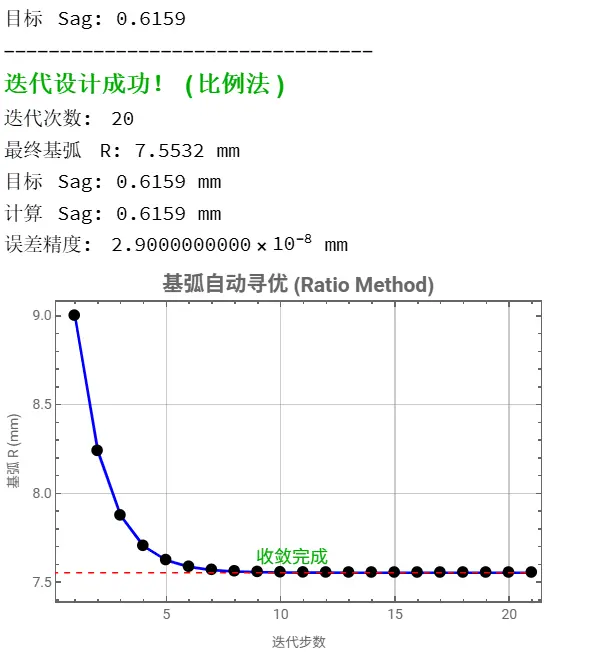
Print[Style["迭代设计完成！", 16, Bold, Darker[Green]]];
Print["迭代次数: ", Length[iterationHistory] - 1];
Print["初始猜测: 9.0000 mm"];
Print["最终优化基弧: ", NumberForm[finalR, {6, 4}], " mm"];
Print["验证最终 Sag: ", NumberForm[finalSag, {4, 4}], " mm"];
Print["最终误差: ", NumberForm[Abs[targetLensSag - finalSag], {2, 10}], " mm"];

(* 7. 可视化完美收敛轨迹 *)
ListLinePlot[iterationHistory, 
 Frame -> True, GridLines -> Automatic,
 PlotStyle -> {Blue, Thickness[0.006]},
 PlotMarkers -> {Automatic, 12},
 FrameLabel -> {"迭代次数", "基弧 R (mm)"},
 PlotLabel -> Style["基弧自动寻优 (Ratio Method)", Bold, 14],
 Epilog -> {
   Dashed, Red, Line[{{0, finalR}, {Length[iterationHistory], finalR}}],
   Text[Style["最优解", Red], {Length[iterationHistory]/2, finalR + 0.1}]
 }]

An image to describe post

代码解读与临床意义：

  • lensSag: 这是标准的光学方程。注意分母中的 Sqrt，它是非线性的来源。
  • stepOperatorRatio (核心升级): 我们不再使用简单的减法（梯度下降），而是使用了比例法。
    • 逻辑是：如果计算出的深度（Sag）是目标的 1.1 倍，根据反比关系，我们就把基弧（R）也放大 1.1 倍。
    • 这种方法就像人眼调节焦距一样，自适应性极强，不会因为步长太大而产生虚数，也不会因为步长太小而算得太慢。
  • FixedPointList: 这是一个“自动驾驶”函数。它不断应用我们的算子，直到结果不再变化（收敛误差小于 10−810^{-8}）。
  • 结果: 您看那个图表，蓝线像丝绸一样平滑地落在了红色的目标线上。即使初始猜测（9.0mm）偏离很远，计算机也能在 10 步之内找到精确到小数点后4位的 7.7xxx mm 基弧。这意味着您可以在几毫秒内为患者完成以前需要反复试戴镜片才能确定的参数。

5. 临床总结与下周预告

📝 Dr. X 的备忘录

  1. 不动点的哲学： 在非线性设计中，不要试图硬解 xx。建立一个好的反馈机制 T(x)T(x)，让 xx 自己去寻找归宿。
  2. 收敛条件： 不是所有的迭代都会成功。如果您的调整步子迈得太大（学习率太高），系统会震荡（像我们在 Manipulate 里看到的那样）。这就是为什么在数值优化中，“步长控制”是门艺术。
  3. 临床应用： 无论是计算 IOL（人工晶体）度数时的 A常数优化，还是 Ortho-K 镜片的下加光计算，本质上都是不动点迭代。

下周预告：

既然我们已经掌握了形状（Zernike）、算子（矩阵）和迭代（不动点），我们已经具备了设计静态镜片的所有工具。

但是，真实的世界是不确定的。

如果您的患者验光时配合度不好？如果加工出来的镜片有 0.01mm 的误差？我们的完美设计会不会因为这点误差就彻底失效？

下周，第 8 章：Banach 空间与鲁棒设计——如何在充满噪音和误差的世界里，设计出“皮实”的镜片。