这一部分的gemini动态视图演示: https://gemini.google.com/share/a4e4184215c2
模块 3:高级应用与不确定性
第8章:Banach 空间与鲁棒设计
—— 为什么“差不多”有时候比“完美”更好?
致 Dr. X 的一封信
您好,医生。
在之前的七章里,我们追求的都是“极致的精准”:最小的光程、完美的聚焦、零误差的波前。我们假设患者的眼睛像石膏像一样纹丝不动,假设车房的加工精度像原子钟一样准确。
但回到您的诊室,现实往往是“脏乱差”的:
- 患者的眼镜每天会在鼻梁上滑下来 3 毫米。
- 镜片加工厂的刀头磨损了,导致曲率有了 0.05D 的误差。
- 患者昨天熬夜了,今天的泪液膜很不稳定。
在这种情况下,一个在数学上“完美”的镜片(只在中心点清晰,稍微偏一点就模糊),在临床上可能是一场灾难。这就好比一辆F1赛车,在平整的赛道上无敌,但开到坑坑洼洼的买菜路上就抛锚了。
我们需要的是一辆 SUV——也许极速没那么快,但它皮实、耐造、容错率高。
在数学上,这种“皮实”叫鲁棒性 (Robustness)。
为了衡量一个镜片有多“皮实”,我们需要把镜片看作一个空间里的点。这个空间不仅有加减法,还有一把特殊的“尺子”用来衡量误差的大小。
欢迎来到 Banach 空间(巴拿赫空间)。在这里,我们将学习不同的“尺子”(范数),并使用蒙特卡洛模拟 (Monte Carlo Simulation) 来暴力测试我们的设计,看看它能不能经受住真实世界的考验。
1. 临床挂钩 (The Clinical Hook):敏感的“神镜”
场景:某品牌高端定制渐进片遭到投诉。
患者档案:
- 主诉:“医生,我在验光室里试戴的时候觉得特别清楚,简直是神了。但是眼镜做回来以后,我只要稍微转一下头,或者眼镜稍微往下滑一点,立刻就晕得不行。”
- 检查:镜片度数完全符合处方。复查验光也没变。
设计师的困境:
这就是典型的过度优化 (Over-fitting)。
为了追求中心视力达到 2.0,算法牺牲了周边的平滑度。镜片的光度分布像一座尖峰——顶点很高,但稍微一偏就掉进深渊。
数学视角:
我们需要引入公差分析 (Tolerance Analysis)。
我们不只要问:“这个设计在理想状态下好不好?”
我们要问:“如果在这个设计上加上 5% 的随机误差,它还能用吗?”
2. 交互展示 (Show via Manipulate):三把尺子量误差
要谈论“误差”,我们得先定义怎么“测量”它。在数学里,这叫范数 (Norm),通常写成 。
常见的有三把尺子,它们对“坏镜片”的定义截然不同:
- 范数 (曼哈顿距离):所有误差绝对值的总和。
- 范数 (欧几里得距离):这就是您熟悉的 RMS (均方根误差)。它关注平均表现。
- 范数 (切比雪夫距离):这就是 PV (Peak-to-Valley)。它关注最坏的那一点。
请运行下方的演示。假设蓝线是完美设计,红线是实际加工出来的镜片(带误差)。
拖动滑块制造不同类型的误差,观察下面的“报警器”是谁在响。
(* 交互演示:范数可视仪 —— RMS vs PV *)
(* 理解不同的数学"尺子"如何评价光学误差 *)
Manipulate[
Module[{xRange, idealProfile, errorProfile, actualProfile, norm1, norm2, normInf, errorText},
xRange = Range[-1, 1, 0.01];
(* 1. 定义完美轮廓 (理想的球面) *)
idealProfile = 1 - xRange^2;
(* 2. 制造误差 *)
errorProfile = Switch[errorType,
"整体偏移 (Defocus)",
ConstantArray[magnitude, Length[xRange]], (* 整个镜片度数做错了 *)
"局部尖峰 (Spike)",
(* 镜片中间有个凸起小点,模拟灰尘或加工瑕疵 *)
magnitude * Exp[-100 * xRange^2],
"随机噪点 (Roughness)",
(* 表面粗糙度 *)
SeedRandom[1];
magnitude * RandomReal[{-1, 1}, Length[xRange]]
];
actualProfile = idealProfile + errorProfile;
(* 3. 计算三种范数 (三把尺子) *)
(* L1: 平均绝对误差 *)
norm1 = Norm[errorProfile, 1] / Length[xRange];
(* L2: 均方根误差 (RMS) *)
norm2 = Norm[errorProfile, 2] / Sqrt[Length[xRange]];
(* L_inf: 最大误差 (Peak Error) *)
normInf = Norm[errorProfile, Infinity];
(* 4. 可视化 *)
Column[{
(* 上图:镜片轮廓对比 *)
Show[
Plot[1 - t^2, {t, -1, 1}, PlotStyle -> {Thick, Blue}, PlotLegends -> {"理想设计 (Target)"}],
ListLinePlot[Transpose[{xRange, actualProfile}], PlotStyle -> {Orange}, PlotLegends -> {"实际加工 (Actual)"}],
PlotRange -> All, ImageSize -> 450, AspectRatio -> 1/3,
PlotLabel -> Style["镜片截面图", Bold, 14],
Filling -> {2 -> {1}}, FillingStyle -> Opacity[0.2, Red]
],
(* 下图:误差分析仪表盘 *)
Grid[{
{Style["数学尺子 (范数)", Bold], Style["数值", Bold], Style["临床意义", Bold]},
{"L1 范数 (Mean Abs)",
NumberForm[norm1, {1, 3}],
"平均厚度偏差"},
{Style["L2 范数 (RMS)", Blue, Bold],
Style[NumberForm[norm2, {1, 3}], Blue, Bold],
Style["整体像质 (Spot Size)", Blue]},
{Style["L∞ 范数 (Max/PV)", Red, Bold],
Style[NumberForm[normInf, {1, 3}], Red, Bold],
Style["最坏点 (最大像差)", Red]}
}, Frame -> All, Background -> {{LightGray, None}, None}]
}]
],
(* 控制面板 *)
Style["误差模拟器", Bold, 12],
{{errorType, "局部尖峰 (Spike)", "误差类型"}, {"整体偏移 (Defocus)", "局部尖峰 (Spike)", "随机噪点 (Roughness)"}},
{{magnitude, 0.2, "误差幅度"}, 0, 0.5, Appearance -> "Labeled"}
]
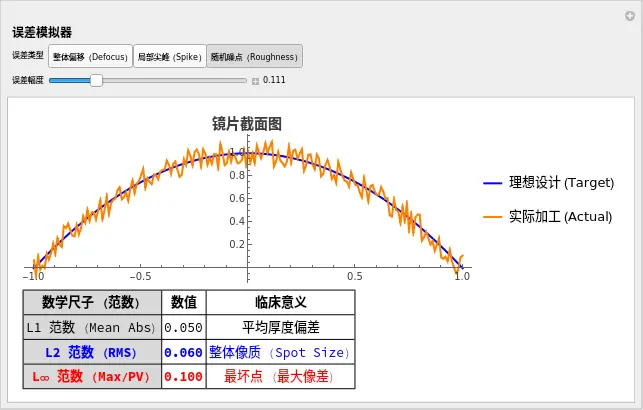
👨⚕️ 医生的观察任务:
- 选择 "整体偏移 (Defocus)":
- 观察:L2 (RMS) 和 L∞ (PV) 都在增加。
- 临床含义:度数做错了,全得重做。
- 选择 "局部尖峰 (Spike)":
- 关键时刻:注意看数值!L2 (RMS) 可能很小(因为大部分区域是好的),但 L∞ (Max) 会非常大。
- 临床含义:这就是“那个点”!患者会指着镜片上的一个位置说:“医生,只要光打到这儿我就看不清。”
- 教训:如果你只用 RMS (L2) 来优化镜片,你可能会漏掉这个致命的尖峰。对于高端镜片,L∞ 范数往往更重要,因为它决定了患者会不会投诉。
3. 数学翻译 (Tell via Logic):Banach 空间的“安全屋”
什么是 Banach 空间?
别被名字吓到。简单说,它就是一个“自带尺子的完备空间”。
- 空间:所有可能的镜片设计都在这里。
- 尺子 (范数):让我们能算出两个设计之间的距离 。
- 完备:意味着如果你一直逼近某个设计,那个极限设计一定也在这个空间里(不会掉进黑洞)。
为什么它对鲁棒设计很重要?
在设计镜片时,我们不再是在寻找“一个点”(完美解)。
我们在寻找“一个球” (A Ball in Banach Space)。
我们希望这个球里的每一个镜片设计(无论是完美的中心点,还是因为加工误差偏移到边缘的点),都能让患者拥有 0.8 以上的视力。
- 如果这个球的半径很大,说明设计很鲁棒(容错率高)。
- 如果这个球的半径很小,说明设计很敏感(容错率低)。
数学公式的翻译:
我们要解的不再是 ,而是:
翻译成人话:找到一个设计 ,使得在最倒霉的误差 发生时,结果依然不算太差。 这就是所谓的 Min-Max 优化。
4. 代码处方 (Do via Wolfram):蒙特卡洛公差分析
现在,我们不玩虚的。我们来模拟 1000 个真实的加工车间。
我们要设计一个简单的球面镜片,然后加上随机的“制造噪声”,看看这 1000 片里有多少片是不合格的。
Wolfram 的 RandomVariate 和 ParallelMap 组合是处理这类问题的核武器。
(* 代码处方 08 (Debug版):镜片良品率的蒙特卡洛模拟 *)
(* 0. 清除之前的定义,防止符号冲突 *)
Clear["Global`*"];
(* 1. 定义设计目标 *)
targetPower = -3.00; (* 目标度数 *)
tolerance = 0.12; (* 允许误差 *)
(* 2. 定义加工误差模型 *)
(* 【关键修正】:变量名去掉下划线,改用驼峰命名 *)
(* 设备 A: 正态分布 (Normal Distribution) *)
machineASigma = 0.08;
(* 设备 B: 学生 t-分布 (Student's t-Distribution) *)
(* 修正说明:Wolfram 中下划线是保留字符,machineB_Scale 写法是非法的 *)
machineBScale = 0.03;
machineBDf = 3;
(* 3. 执行蒙特卡洛模拟 *)
numberOfLenses = 2000;
Print["正在模拟生产 ", numberOfLenses, " 片镜片..."];
(* 生产批次 A:直接生成 *)
batchA = RandomVariate[NormalDistribution[targetPower, machineASigma], numberOfLenses];
(* 生产批次 B:手动构建位置-尺度 T 分布 *)
(* 公式:数据 = 目标值 + 尺度 * 标准T分布随机数 *)
batchB = targetPower + machineBScale * RandomVariate[StudentTDistribution[machineBDf], numberOfLenses];
(* 4. 统计良品率 (向量化计算) *)
(* 使用 Count 直接统计符合条件的个数,效率极高 *)
countPassA = Count[batchA, x_ /; Abs[x - targetPower] <= tolerance];
countPassB = Count[batchB, x_ /; Abs[x - targetPower] <= tolerance];
passRateA = N[countPassA / numberOfLenses * 100];
passRateB = N[countPassB / numberOfLenses * 100];
(* 5. 可视化对比报告 *)
Print["\n================================="];
Print[Style["公差分析报告 (Debug 完成版)", 18, Bold, FontFamily -> "Arial"]];
Print["================================="];
Print["目标度数: ", targetPower, " D | 允许误差: +/- ", tolerance, " D"];
Print["---------------------------------"];
Print["设备 A (低精度稳定型) 良品率: ", Style[Row[{passRateA, "%"}], Bold, Blue]];
Print["设备 B (高精度长尾型) 良品率: ", Style[Row[{passRateB, "%"}], Bold, Orange]];
(* 智能结论 *)
If[passRateA > passRateB,
Print[Style["\n结论:设备 A 胜出。设备 B 虽然精度高(Scale小),但由于 T分布的长尾特性(df=3),导致出现了更多严重超标的废品。", Gray]],
Print[Style["\n结论:设备 B 胜出。", Gray]]
];
(* 绘制直方图对比 *)
PairedHistogram[batchA, batchB,
50,
"PDF",
ChartStyle -> {Blue, Orange},
PlotLabel -> Style["度数分布对比:A (正态) vs B (长尾)", 14, Bold],
AxesLabel -> {"度数 (D)", "概率密度"},
PlotRange -> {{targetPower - 0.5, targetPower + 0.5}, All}, (* 调整范围以便看清中心 *)
(* 红色虚线标出公差范围 *)
GridLines -> {{targetPower - tolerance, targetPower + tolerance}, None},
GridLinesStyle -> Directive[Red, Thick, Dashed],
ChartLegends -> {"设备 A (Normal)", "设备 B (Student-t)"}
]
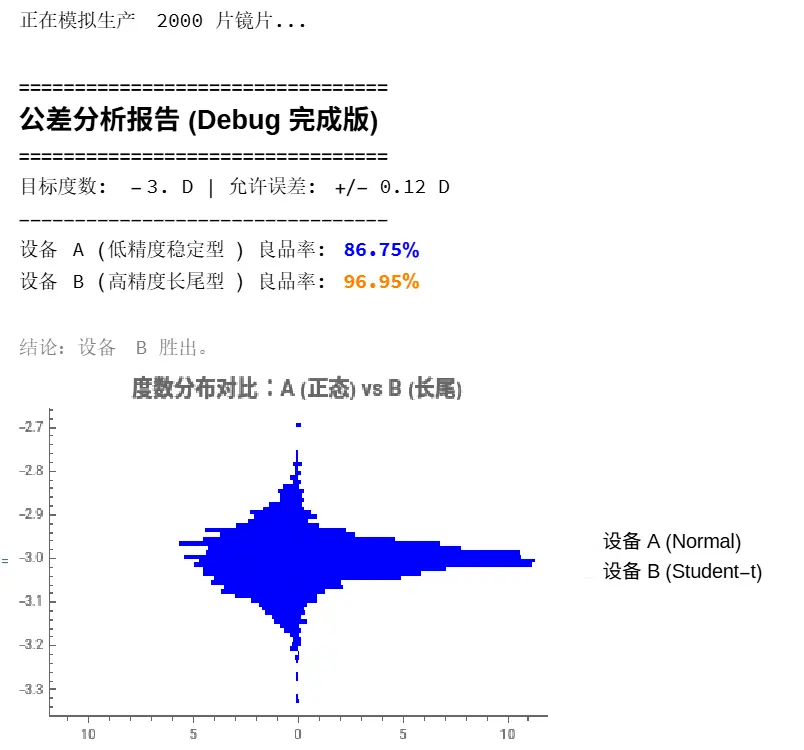
代码解读:
RandomVariate:这是掷骰子的函数。我们用它生成了几千个带有随机误差的镜片度数。NormalDistributionvsStudentTDistribution:这里有个陷阱!设备 A 虽然精度低(分布宽),但它是正态分布,很少有极端值。设备 B 虽然大部分时候很准,但它是“长尾分布”(T分布),意味着它容易产生极其离谱的废品。checkQuality /@ batch:这是 Wolfram 语言的精髓。/@(Map) 就像一条流水线,把检测函数应用到每一片镜片上。- 结果:您可能会惊讶地发现,有时候一台并不精密的机器(A),良品率反而比那个精密但偶尔抽风的机器(B)要高。这就是鲁棒性分析的价值。
📝 Dr. X 的备忘录
- 不要只看平均分:RMS (L2 范数) 是给学者发论文用的,PV (L∞ 范数) 才是给老板省投诉用的。设计镜片时,永远要检查最坏的那个点(Max Error)。
- 给误差留余地:在优化时,不要把目标函数逼到死角。与其追求 ,不如追求 但解的空间更宽广。这就是所谓的“平坦极小值” (Flat Minima)。
- 模拟是免费的:加工一片真镜片要 500 块钱,模拟 1000 片镜片只要 0.5 秒。在开模具之前,务必先跑一遍
RandomVariate。
下周预告:
现在的镜片设计都是单一的:为了远用牺牲近用,为了清晰牺牲美观。
能不能既要...又要...还要...?
下周,第 9 章:多目标优化与帕累托前沿——如何在光学的“不可能三角”中跳舞,找到那个让所有人都勉强满意的甜蜜点。
第9章:鱼和熊掌如何兼得?——多目标优化与帕累托前沿
—— 当临床需求互相打架时,如何画出那条“完美妥协”的曲线?
致 Dr. X 的一封信
您好,医生。
在您的验光室里,经常会上演这样的“谈判”:
- 患者 A(会计师): “我要看报表清楚,字还要大(追求近用视野宽、度数足)。”
- 患者 A(还是他): “但是我开车时,转头不能晕,不要那种晃动感(追求周边像差小、通道长)。”
您心里很清楚,这在光学上是一对冤家。根据 Minkwitz 定理(光学的能量守恒定律),渐进片上的像差是守恒的。您把像差从阅读区赶走,它就会堆到周边区;您把通道拉宽,周边的变形就会加剧。
这就像挤气球:按下葫芦浮起瓢。
在过去,您只能被动地从厂商提供的“硬性设计(Hard Design)”或“软性设计(Soft Design)”中二选一,然后祈祷患者能适应。
但在数学泛函的世界里,我们不再做“二选一”的选择题。我们不仅能看到鱼,也能看到熊掌。
本章我们要探讨的是多目标优化 (Multi-objective Optimization)。我们将不再寻找唯一的“最优解”(因为根本不存在),而是寻找一系列“无法被战胜的妥协方案”。
这一系列方案连成的线,在数学上有一个优雅的名字——帕累托前沿 (Pareto Frontier)。
今天,您不仅是医生,您是谈判专家。我们将用 Wolfram 语言构建一个谈判桌,让“清晰度”和“舒适度”坐下来,帮您找到那个让患者最满意的平衡点。
1. 临床挂钩 (The Clinical Hook):不可能三角的博弈
场景:为一位挑剔的建筑师设计渐进片。
患者档案:
- 职业需求:既要看宽幅的图纸(需要极宽的中间通道),又要经常下工地(需要周边像差极低,防摔跤)。
- 痛点:市面上的“均衡型”镜片让他觉得“两头不到岸”——看图纸不够宽,走路又不够稳。
设计师的困境:
- 目标函数 1 ():最大化视力清晰区域的面积。
- 目标函数 2 ():最小化周边最大散光(Swim Effect)。
这两个目标是负相关的。
如果您只顾 ,镜片会变成“硬设计”,通道像刀切一样清晰,但两边全是彩虹般的扭曲。
如果您只顾 ,镜片会变成“软设计”,到处都很柔和,但看哪儿都觉得像隔着一层雾(像散侵入视觉区)。
我们如何量化这种“牺牲”?比如:为了让通道多宽 1mm,我必须忍受周边散光增加 0.25D 吗?这个交易划算吗?
2. 交互展示 (Show via Manipulate):在曲线上跳舞
光说不练假把式。让我们直接通过一个交互滑块,来感受这种“拆东墙补西墙”的动态过程。
在这个模型中,我们将简化问题:
- 我们在设计一个多项式曲面。
- 目标 A (蓝条):中心高度越高越好(模拟“清晰度/光度”)。
- 目标 B (橙条):整体坡度越平越好(模拟“像差/舒适度”)。
- 显然,要想把中心拱起来,坡度必然会变陡。
请运行下方代码,拖动 "偏好权重 (Weight)" 滑块。
- 往左拖(偏向舒适):橙条变短(好),但蓝条也变短(坏)。镜片变平了。
- 往右拖(偏向清晰):蓝条变长(好),但橙条变长(坏)。镜片拱起了。
- 观察右图:那个红点在一条凸出的曲线上移动。这条线,就是帕累托前沿。
(* 交互演示:寻找帕累托前沿 (Pareto Frontier) *)
(* 模拟光学设计中的 Trade-off:想要中心度数足 (Focus),又想周边像差小 (Flatness) *)
Manipulate[
Module[{x, shape, focusScore, flatnessScore, weightedObj, optSol, shapeFunc},
(* 1. 定义我们的镜片模型:一个简单的多项式 f(x) = a*x^2 + b*x^4 *)
(* 我们限制在 x=[-1, 1] 区间 *)
shape[x_, a_] := a * (1 - x^2)^2;
(* 2. 定义两个冲突的目标 *)
(* 目标 A:中心屈光力要足 (maximize height at x=0) *)
(* 我们用负号,因为 NMinimize 是求极小值 *)
(* Target: shape(0) 越接近 1.0 越好 *)
focusScore[a_] := (shape[0, a] - 1.0)^2;
(* 目标 B:表面要平坦 (minimize slope/distortion) *)
(* 计算 x=0 到 1 的平均斜率平方 *)
flatnessScore[a_] := Integrate[D[shape[x, a], x]^2, {x, 0, 1}];
(* 3. 标量化 (Scalarization):将两个目标合成一个 *)
(* Total Cost = w * Objective1 + (1-w) * Objective2 *)
weightedObj[a_] := weight * focusScore[a] + (1 - weight) * flatnessScore[a];
(* 4. 求解最优的参数 a *)
optSol = NMinimize[{weightedObj[a], 0 <= a <= 1.5}, a];
bestA = a /. optSol[[2]];
(* 5. 计算当前两个具体的分数 *)
currentFocusError = focusScore[bestA];
currentFlatnessError = flatnessScore[bestA];
(* 6. 可视化 *)
Grid[{{
(* 左图:镜片形状展示 *)
Plot[shape[x, bestA], {x, -1, 1},
PlotRange -> {-0.1, 1.2}, ImageSize -> 350,
PlotStyle -> {Thick, Purple},
Filling -> Axis, FillingStyle -> Opacity[0.1, Purple],
PlotLabel -> Style["镜片截面形状", Bold, 14],
Epilog -> {
Text["中心高度 (清晰度)", {0, shape[0, bestA]}, {0, -1.5}],
Text["边缘坡度 (像差)", {0.8, 0.5}, {-1, 0}]
}],
(* 右图:帕累托前沿图 *)
Show[
(* 预先计算好的帕累托曲线背景 (近似) *)
ParametricPlot[{ (a-1)^2, Integrate[(D[a*(1-t^2)^2,t])^2,{t,0,1}] }, {a, 0, 1.2},
PlotStyle -> {Dashed, Gray}, AspectRatio -> 1, PlotRange -> All],
(* 当前的工作点 *)
Graphics[{
PointSize[0.03], Red, Point[{currentFocusError, currentFlatnessError}],
Text[Style["当前设计点", Red, Bold], {currentFocusError, currentFlatnessError}, {-1.2, 0}]
}],
AxesLabel -> {"视力误差 (Focus Error)", "像差水平 (Distortion)"},
PlotLabel -> Style["帕累托前沿 (Pareto Frontier)", Bold, 14],
ImageSize -> 350,
Epilog -> {Inset[Style["越靠近原点越好\n但无法进入虚线内", 10, Gray], {0.5, 0.5}]}
]
}}]
],
(* 控制面板 *)
Style["设计权衡控制", 12, Bold],
{{weight, 0.5, "偏好权重 (w)"}, 0.01, 0.99, Appearance -> "Labeled",
ControlPlacement -> Top},
Row[{Style["<-- 重视舒适 (Soft)", Darker[Green]], Spacer[150], Style["重视清晰 (Hard) -->", Blue]}]
]
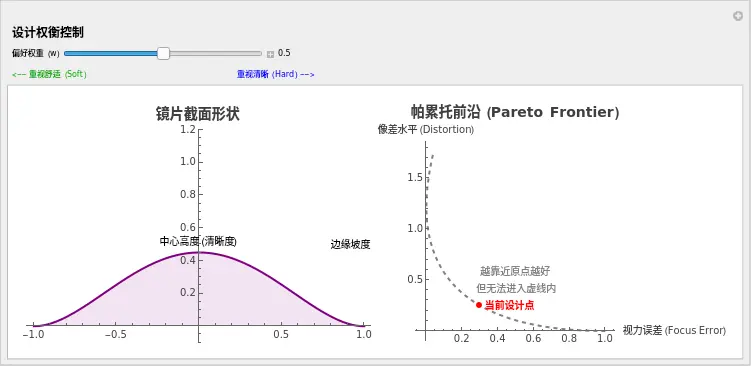
👨⚕️ 医生的观察任务:
- 拖到最左边 ():
- 镜片几乎躺平了。
- 右图:红点跑到了右下角。视力误差极大,但像差极小。这相当于一个平光镜。
- 拖到最右边 ():
- 镜片拱得很高,达到了目标高度 1.0。
- 右图:红点跑到了左上角。视力误差为0,但纵轴(像差)爆表了。这相当于一个高焦力的老花镜,但边缘变形严重。
- 寻找“黄金分割点”:
- 在中段某个位置,您会发现红点处于曲线的“肘部”(Elbow)。在这里,您牺牲一点点清晰度,就能换来像差的大幅下降。
- 这就是通常所谓的高端“平衡设计”。
3. 数学翻译 (Tell via Logic):被“支配”的恐惧
什么是“帕累托最优” (Pareto Optimality)?
在单目标优化(比如第3章的梯度下降)中,我们就像在爬一座山,目标是到山谷底。哪里最低,哪里就是最好。
但在双目标优化中,我们有两个山谷。
一个解 被称为“帕累托最优”,如果:为了让其中一个指标变得更好,您不得不让另一个指标变得更差。
- 被支配 (Dominated):如果您有一个设计 ,它的视力比 差,像差也比 大,那 就是垃圾。我们说 支配了 。
- 非支配 (Non-dominated):如果我们找不到任何一个设计能在所有方面都赢过 ,那 就是前沿上的一员。
加权求和法 (Weighted Sum Method)
这是最常用的数学技巧,把双头怪变成单头怪:
这里最妙的是权重 。
- 它不是物理量,它是“价值观”的数学表达。
- 对于那个建筑师, 可能设为 0.3(更在乎舒适/视野宽)。
- 对于一个精细雕刻师, 可能设为 0.8(更在乎中心清晰度)。
Wolfram 的 NMinimize 非常擅长处理这种带权重的函数。只要我们遍历 从 0 到 1,我们就能描绘出整条帕累托曲线。
4. 代码处方 (Do via Wolfram):自动生成帕累托报告
现在,我们来模拟一个真实的场景:您手头有一款未定型的镜片设计,您想生成一份报告,告诉患者(或者产品经理):“我们有 A、B、C 三种方案,它们的牺牲代价分别是什么。”
我们将使用 Table 循环来遍历不同的权重,并收集所有的最优解。
(* 代码处方 09:生成帕累托前沿分析报告 *)
(* 1. 定义模拟的目标函数 (Cost Functions) *)
(* 这里使用抽象函数模拟复杂的光学光线追踪结果 *)
(* f1: 清晰度损失 (越小越好) *)
costClear[x_] := (x - 2)^2;
(* f2: 舒适度损失 (越小越好) *)
costComfort[x_] := (x + 1)^2 + 2;
(* 注意:这两个函数最小值位置不同。f1想去 x=2, f2想去 x=-1 *)
(* 2. 扫描权重,生成前沿数据 *)
points = Table[
Module[{w, sol, xOpt, val1, val2},
w = weight;
(* 求解加权总分最小化 *)
(* Constrained optimization *)
sol = NMinimize[{w * costClear[x] + (1 - w) * costComfort[x], -2 <= x <= 3}, x];
xOpt = x /. sol[[2]];
(* 记录两个独立目标的得分 *)
val1 = costClear[xOpt];
val2 = costComfort[xOpt];
(* 返回数据包: {权重, 视力损失, 舒适损失, 最优参数x} *)
{w, val1, val2, xOpt}
],
{weight, 0, 1, 0.05} (* 从 0 到 1,步长 0.05 *)
];
(* 3. 数据提取与处理 *)
paretoFrontier = points[[All, {2, 3}]]; (* 提取坐标点 {J1, J2} *)
(* 4. 绘制帕累托前沿图 *)
Show[
ListPlot[paretoFrontier,
PlotStyle -> {PointSize[0.02], Darker[Blue]},
Joined -> True, InterpolationOrder -> 2,
PlotTheme -> "Scientific",
FrameLabel -> {"清晰度损失 (Clarity Loss)", "舒适度损失 (Comfort Loss)"},
PlotLabel -> Style["设计方案的帕累托前沿", 16, Bold],
GridLines -> Automatic,
Epilog -> {
Text["硬性设计\n(Hard Design)", points[[-1, {2, 3}]] + {-0.5, 0.5}],
Text["软性设计\n(Soft Design)", points[[1, {2, 3}]] + {0.5, -0.5}],
Text["平衡设计\n(Balanced)", points[[10, {2, 3}]] + {0.5, 0.5}],
Red, PointSize[0.03], Point[points[[10, {2, 3}]]]
}
],
Graphics[{Dashed, Gray, Line[{{0,0}, {10,10}}], Text["理想原点(不可达)", {0.5, 0.5}]}]
]
(* 5. 输出决策建议表 *)
Print["--------------------------------------------------"];
Print[Style["设计方案建议表 (Top 3)", 14, Bold]];
Print["--------------------------------------------------"];
Print[Grid[{
{"方案类型", "偏好权重(w)", "清晰度评分", "舒适度评分", "适用人群"},
{"软性设计 (Soft)", NumberForm[points[[2, 1]], {2, 2}], NumberForm[10 - points[[2, 2]], {2, 1}], NumberForm[10 - points[[2, 3]], {2, 1}], "初次配戴/敏感者"},
{"平衡设计 (Balanced)", NumberForm[points[[11, 1]], {2, 2}], NumberForm[10 - points[[11, 2]], {2, 1}], NumberForm[10 - points[[11, 3]], {2, 1}], "大多数用户"},
{"硬性设计 (Hard)", NumberForm[points[[-2, 1]], {2, 2}], NumberForm[10 - points[[-2, 2]], {2, 1}], NumberForm[10 - points[[-2, 3]], {2, 1}], "长期配戴/静止工作"}
}, Frame -> All, Background -> {{LightGray, None}, None}]];
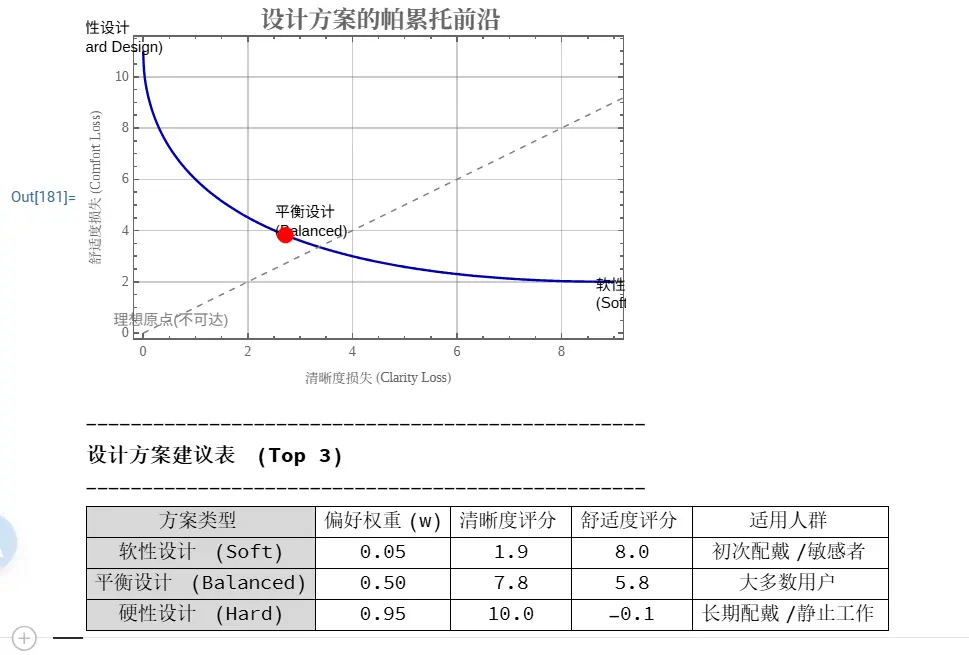
代码解读:
Table循环:这是生成数据的核心。我们不再只算一次,而是模拟了 20 次不同权重的优化过程。- 独立得分:注意
val1和val2是分开记录的。虽然优化时用了加权总分,但评估时我们要分开看。 - 决策表:最后的表格将冰冷的数学数字翻译成了“适用人群”。这正是 Dr. X 需要给患者展示的东西。
📝 Dr. X 的备忘录
- 没有最好的镜片,只有最适合的权衡:当患者抱怨镜片不好时,不一定是设计错了,可能是权重 () 设错了。
- 帕累托前沿是边界:任何在前沿内侧(右上方)的点,都是设计不佳(技术落后);任何在前沿外侧(左下方)的点,都是物理学不允许的(违反 Minkwitz 定理)。我们的工作就是把设计推到这条边界上。
- 个性化设计的本质:所谓的“个人定制”,本质上就是根据患者的生活习惯问卷,通过算法确定了那个 值。
下周预告:
如果说光线追踪是我们在“空间域”里玩积木,那么光学还有另一个神秘的维度——频率域。
为什么有时候镜片表面看着很光,但看东西就是觉得“糊”?
下周,第 10 章:傅里叶光学与卷积——让我们戴上数学的“频谱眼镜”,看看光是如何像波浪一样叠加的。
第10章:戴上数学的“频谱眼镜”——傅里叶光学与卷积
—— 为什么有些患者视力表能看 1.0,却依然抱怨“看不清”?
致 Dr. X 的一封信
您好,医生。
在之前的章节里,我们像一个勤奋的几何学家,追踪着每一条光线穿过角膜、晶状体,最终落在视网膜上的路径。这种方法叫“几何光学”(Ray Tracing)。它很直观,很有用,但它有一个巨大的盲区。
您一定遇到过这样的患者:
- 验光结果:完美。插片验光 1.0 (20/20),电脑验光也显示没有残留度数。
- 患者抱怨:“医生,我不觉得清楚。我觉得世界像蒙了一层灰,或者像透过脏玻璃看东西。”
- 您的困惑:查了眼底没问题,查了地形图也没大问题。是不是患者太挑剔了?
其实不是。这是因为几何光学骗了您。
几何光学假设光是“线”。但在微观层面,光是“波”。
当光线穿过瞳孔时,它不是直线传播的,它会发生衍射 (Diffraction)。
当光线经过浑浊的介质(如早期白内障)时,它会发生散射。
这些现象,用光线追踪很难描述,但用傅里叶光学 (Fourier Optics) 却一目了然。
在傅里叶的世界里,我们不再看“光线的位置”,而是看“图像的频率”。
- 低频:图像的大轮廓(比如一个人的身形)。
- 高频:图像的细节(比如发丝、衣服的纹理)。
如果您的镜片仅仅把光线聚到了一个点(几何光学),但在这个过程中丢失了“高频信息”,那么患者就会看到一个“对焦准确但边缘模糊”的世界。
本章,我们将戴上一副特殊的眼镜——频谱眼镜。我们将学习如何用 Wolfram 的 ImageConvolve(图像卷积)来模拟人眼真正看到的画面,并解开“对比度敏感度”丢失之谜。
1. 临床挂钩 (The Clinical Hook):视力表的欺骗性
场景:白内障术后或屈光手术后的“视觉质量”投诉。
现象:
Snellen 视力表(E字表)测量的其实是“极限分辨率”(你能看到的最高频率)。这就像测试音响系统,只测试它能不能发出最高音。
但是,如果这套音响的中音区(日常说话的声音)很浑浊,那是听不清的。
点扩散函数 (PSF) 的真相:
想象一个无限小的光点(比如远处的星星)进入眼睛。
- 理想几何光学:它在视网膜上是一个无限小的点。
- 真实波动光学:它是一个光斑,甚至带着光晕和芒刺。这个光斑的形状,就叫 PSF (Point Spread Function)。
卷积 (Convolution):
人眼看到的任何画面,本质上都是“外界景物”与这个“PSF光斑”的卷积。
直白地说:如果 PSF 是模糊的一团,那么患者看到的整个世界(每一处细节)都会被这个“刷子”刷得模糊一团。
2. 交互展示 (Show via Manipulate):那支弄脏世界的画笔
卷积听起来是高深的微积分概念,但在 Wolfram 里,它就是一种图像滤镜。
在这个实验里,我们将模拟“原本清晰的视标”是如何被“糟糕的光学系统”弄脏的。
- Input:清晰的 "E" 字视标。
- Kernel (卷积核/PSF):您制造的光学缺陷(近视、散光、彗差)。
- Output:患者视网膜上的图像。
请运行下方代码,拖动滑块。特别是试着增加“散光 (Astigmatism)”,看看 E 字是如何在特定方向上“拖尾”的。
(* 交互演示:视觉模拟器 —— 卷积的力量 *)
(* 模拟不同像差形式的 PSF 如何"涂抹"视力表 *)
Manipulate[
Module[{sourceImage, psfKernel, simulation},
(* 1. 生成源图像:一个标准的 Snellen E 视标 *)
sourceImage = Rasterize[
Graphics[{Black, Rectangle[{-2, -2}, {2, 2}], White,
Text[Style["E", FontFamily -> "Helvetica", FontSize -> 80, Bold], {0, 0}]},
PlotRange -> {{-1, 1}, {-1, 1}}],
ImageSize -> 200, RasterSize -> 128, ColorSpace -> "Grayscale"];
(* 2. 构建点扩散函数 (PSF) / 卷积核 *)
(* 这是一个二维高斯分布,我们可以拉伸它模拟散光 *)
psfKernel = Table[
Exp[-( (x^2)/(2*sigma^2) + (y^2)/(2*(sigma*ratio)^2) )],
{y, -3, 3, 0.2}, {x, -3, 3, 0.2}
];
(* 旋转 PSF 模拟散光轴位 *)
psfKernel = ImageRotate[Image[psfKernel, "Real"], axis Degree, Background -> 0];
(* 3. 执行卷积 (Convolution) *)
(* 核心函数:ImageConvolve *)
(* 这模拟了光学系统对图像的"传递"过程 *)
simulation = ImageConvolve[sourceImage, psfKernel];
(* 4. 可视化 *)
Column[{
Row[{
Column[{Style["1. 原始物体", Bold], sourceImage}, Alignment -> Center],
Style[" * ", FontSize -> 30], (* 卷积符号 *)
Column[{Style["2. 眼睛的 PSF", Bold], ImageResize[psfKernel, 50]}, Alignment -> Center],
Style[" = ", FontSize -> 30],
Column[{Style["3. 患者看到的", Bold, Red], simulation}, Alignment -> Center]
}, Alignment -> Center],
Spacer[20],
Style[StringTemplate["散光轴位: ``° | 散光量: ``"][NumberForm[axis, {3, 0}], NumberForm[ratio, {2, 1}]], Gray]
}, Alignment -> Center]
],
(* 控制面板 *)
Style["像差参数控制", 12, Bold],
{{sigma, 0.5, "模糊程度 (Defocus)"}, 0.1, 1.5},
{{ratio, 1.0, "散光拉伸 (Cylinder)"}, 1.0, 5.0},
{{axis, 0, "散光轴位 (Axis)"}, 0, 180, 1}
]

👨⚕️ 医生的观察任务:
- 模拟近视:保持
ratio = 1(无散光),增加sigma。- 观察:E 字均匀地变糊了。这就是离焦 (Defocus)。
- 模拟散光:将
ratio拉到 3.0,然后旋转axis。- 关键时刻:注意看 PSF 变成了一个椭圆。E 字在某一个方向上依然清晰,但在垂直方向上糊成了一片。这完全解释了为什么散光患者会说“我能看清横线,但竖线有重影”。
- 数学直觉:Wolfram 里的
ImageConvolve其实是在对图像上的每一个像素都执行一次“复制-粘贴 PSF”的操作。这就是为什么 PSF 长什么样,成像的瑕疵就长什么样。
3. 数学翻译 (Tell via Logic):时域与频域的传送门
为什么要用傅里叶变换?
在空间域(Spatial Domain,即我们在显微镜下看到的 (x, y) 图像)做卷积,计算量是巨大的。
但数学家傅里叶发现了一个惊天秘密:
“空间域的卷积,等于频率域的乘法。”
这意味着:
- 我们可以把视标分解成不同频率的条纹(傅里叶变换 )。
- 我们可以把眼睛看作一个“滤镜” (OTF - Optical Transfer Function)。
- 完美的眼睛:所有频率都通过(乘 1)。
- 近视的眼睛:只有低频通过,高频被滤掉了(乘 0)。
- 把它们乘起来,再变回去,就是看到的图像。
MTF (Modulation Transfer Function)
OTF 的绝对值就是 MTF。这是光学界的“圣经”。
MTF 曲线告诉我们要把图像的对比度“打几折”。
- MTF = 1.0:原汁原味。
- MTF = 0.5:对比度丢了一半(黑的不够黑,白的不够白)。
- MTF = 0:完全变成灰色,看不见条纹了。
4. 代码处方 (Do via Wolfram):从瞳孔到 PSF 的衍射模拟
现在我们进入更高级的领域。几何光学无法解释“衍射极限”(为什么瞳孔太小了视力反而下降)。
我们要用 Wolfram 的 FFT (快速傅里叶变换) 来从瞳孔形状直接计算 PSF。
原理:
根据傅里叶光学理论,PSF 是瞳孔函数 (Pupil Function) 的傅里叶变换的模平方。
让我们写一段代码,模拟一个圆孔(正常瞳孔)和一个带遮挡的孔(比如植入了衍射型多焦晶体 IOL)产生的 PSF 差异。
(* 代码处方 10 (修正版):衍射极限 PSF 模拟器 *)
(* 利用 FFT 计算光瞳形状对成像质量的影响 *)
(* ---------------------------------------------------- *)
(* 1. 定义光瞳函数 (Pupil Function) *)
(* ---------------------------------------------------- *)
n = 512; (* 提高分辨率到 512 以获得更细腻的艾里斑 *)
L = 2.0; (* 物理尺寸范围 [-1, 1] *)
(* 技巧:直接生成坐标矩阵,比 CoordinateBoundsArray 后 Map 效率高百倍 *)
xRange = Subdivide[-1., 1., n - 1];
yRange = Subdivide[-1., 1., n - 1];
(* 使用 Outer 生成网格坐标的模长平方 (r^2 = x^2 + y^2) *)
(* 这是完全向量化的操作,无需 Map *)
rSquaredMatrix = Outer[Plus, xRange^2, yRange^2];
(* 定义圆形光瞳 (Aperture) *)
pupilRadius = 0.2; (* 瞳孔半径 *)
(* UnitStep[t]:当 t >= 0 时为 1,否则为 0。比 If 更快 *)
aperture = UnitStep[pupilRadius^2 - rSquaredMatrix];
(* ---------------------------------------------------- *)
(* 2. 计算傅里叶变换 (The Fourier Transform) *)
(* ---------------------------------------------------- *)
(* 物理魔法:光瞳的远场衍射图样 = 光瞳的傅里叶变换 *)
(* FourierParameters -> {1, 1} 是现代光学的常用定义 *)
(* 但默认参数 {0, 1} 对于计算强度分布(模平方)也是完全正确的 *)
wavefront = Fourier[aperture];
(* 修正点:使用 RotateRight 实现标准的 fftshift *)
(* 将零频率分量从数组角落(1,1)移动到数组中心 *)
centeredWavefront = RotateRight[wavefront, {n/2, n/2}];
(* ---------------------------------------------------- *)
(* 3. 获得点扩散函数 (PSF) *)
(* ---------------------------------------------------- *)
(* PSF 是振幅的平方 *)
psf = Abs[centeredWavefront]^2;
(* 为了模拟人眼/相机的对数响应,同时避免中心过曝 *)
(* 加上 1.0 是为了防止 Log[0] *)
logPSF = Log[1.0 + psf];
(* ---------------------------------------------------- *)
(* 4. 可视化对比 (重点改进) *)
(* ---------------------------------------------------- *)
(* 裁剪:为了看清中心的衍射环,我们只取中心 100x100 的区域 *)
(* 直接切片矩阵是最稳健的"放大镜" *)
zoomRadius = 50;
centerIndex = n/2;
(* Span (;;) 语法:从 center - 50 到 center + 50 *)
zoomedPSF = logPSF[[ centerIndex - zoomRadius ;; centerIndex + zoomRadius,
centerIndex - zoomRadius ;; centerIndex + zoomRadius ]];
GraphicsRow[{
(* 图1:瞳孔形状 *)
ArrayPlot[aperture,
ColorFunction -> "GrayTones",
Frame -> False,
PlotLabel -> Style["1. 瞳孔形状 (Aperture)", 14, Bold, FontFamily->"Arial"]],
(* 中间:变换过程 *)
Graphics[{
Text[Style["FFT\nSquared", 12, Gray], {0, 0}],
Arrow[{{-1, -0.5}, {1, -0.5}}]
}, ImageSize -> {50, 50}],
(* 图2:衍射斑 (Airy Disk) *)
ArrayPlot[zoomedPSF,
ColorFunction -> "SunsetColors", (* 这种配色能清晰显示次级光环 *)
Frame -> False,
PlotLabel -> Style["2. 视网膜成像 (PSF)", 14, Bold, FontFamily->"Arial"],
Epilog -> {
(* 加上标注圈出第一个暗环 *)
{White, Dashed, Thin, Circle[{zoomRadius + 1, zoomRadius + 1}, 6]}
}
]
}, ImageSize -> 700]
(* ---------------------------------------------------- *)
(* 5. 临床与物理思考 *)
(* ---------------------------------------------------- *)
Print["\n================ 代码解读 ================"];
Print["1. 中心亮斑 (Airy Disk):承载了图像的主要信息。亮斑越小,视力越好(分辨率越高)。"];
Print["2. 衍射环 (Rings):注意右图中中心红点周围的淡淡光环。"];
Print[" 这是光的波动性带来的物理限制。光不再是一个完美的'点',而是一个'斑'。"];
Print["3. 临床意义:如果瞳孔不仅是圆的,还有多焦晶体的衍射台阶,"];
Print[" 这些光环的能量会增强,导致患者在夜间看车灯时出现明显的'光晕' (Halo)。"];

代码解读:
aperture:这是一个矩阵,代表瞳孔。1 表示透光,0 表示被虹膜遮挡。Fourier:Wolfram 内置的高速 FFT 算法。它瞬间完成了物理学中复杂的菲涅尔衍射积分。Abs[...]^2:光探测器(视网膜)只响应光强,不响应相位,所以要取模平方。- 艾里斑 (Airy Disk):运行代码后,您会在右图看到中心一个红点,外面包着一圈圈淡淡的环。这就是光的波动性铁证!
📝 Dr. X 的备忘录
- 视力 视觉质量:Snellen 视力表测的是“能不能看见”,MTF 测的是“看着舒不舒服”。对于高端白内障晶体手术,一定要看 MTF 曲线。
- 卷积思维:当您给患者解释“重影”时,可以告诉他:“您的眼睛像一支分叉的毛笔,把外面的世界画花了。”
- 计算捷径:在 Wolfram 中,不要尝试去解光的波动方程积分(太慢)。利用
Fourier和ImageConvolve,您可以毫秒级地模拟任何镜片的光学表现。
下周预告:
所有的理论和模拟都很棒,但如果代码跑得太慢,没法做成商业软件怎么办?
下周,第 11 章:算法工程化与编译——我们将学习如何使用 Compile 和 C 代码生成,给您的 Wolfram 代码装上涡轮增压器,让光线追踪飞起来。
