这一部分的gemini 动态视图演示: https://gemini.google.com/share/98f3eaea066c
第四部分:云端部署与未来
第11章:给你的代码装上涡轮——算法工程化与编译
—— 当光线追踪需要处理 100 万条光线时,如何让电脑不卡死?
致 Dr. X 的一封信
您好,医生。
回顾一下第 10 章,我们为了模拟真实的视觉效果,用卷积“弄脏”了图像。虽然效果很酷,但您可能注意到了一个尴尬的细节:按下 Shift+Enter 后,电脑的风扇开始狂转,屏幕上出现了一个蓝色的圆圈转啊转,过了整整 5 秒钟图才出来。
您可能会想:“如果我把这个软件发给病人用,他们能忍受每次点击都要等 5 秒吗?”
显然不能。在临床软件中,速度就是体验,速度就是信任。一个卡顿的界面会让人觉得计算结果也不可靠。
为什么 Wolfram 语言有时候会慢?
因为它太“聪明”了。
当您输入 a + b 时,Wolfram 内核像一位细心的全科医生,它会先检查:a 是整数吗?是复数吗?是图像吗?是一个公式吗?
这种“通用性检查”消耗了大量时间。
但在做光线追踪时,我们不需要全科医生,我们需要一位外科专家。我们很清楚 a 和 b 就是坐标数字(浮点数)。我们不需要检查,我们只需要计算。
本章,我们将学习如何签署“免责协议”——使用 Compile (编译) 功能。
我们将告诉 Wolfram:“别管数据类型了,我保证它们都是数字,请用 C 语言的速度全速跑起来!”
这一步,是将您的“实验笔记”变成“商业软件”的关键跨越。
1. 🩺 临床挂钩:从“演示”到“引擎”
场景:您设计了一款“近视防控离焦镜片”的模拟器。
现状:
- 为了准确评估离焦量,您需要在瞳孔区追踪 10,000 条光线。
- 使用普通的 Wolfram 代码,处理一条光线需要 0.001 秒。
- 算完一幅图需要 10 秒。
- 如果想做成视频(每秒 30 帧),那简直是天方夜谭。
目标:
我们需要将计算速度提升 100 倍到 1000 倍,实现实时渲染 (Real-time Rendering)。
当您拖动镜片曲率的滑块时,光斑图必须像水流一样流畅地变化,没有任何延迟。
只有这样,您的工具才能从“科研代码”变成医生案头的“生产力工具”。
2. 🎛 交互展示:解释型 vs. 编译型
让我们来一场赛跑。
我们将执行一个简单的数学任务:计算 。
- 选手 A (蓝色):普通的 Wolfram 代码(解释执行)。
- 选手 B (红色):编译后的代码(机器码执行)。
请运行下方代码,点击 "开始赛跑 (Start Race)"。
注意看下方的“耗时”对比。
(* 交互演示:速度赛跑 —— 解释器 vs 编译器 *)
(* 感受 Compile 带来的性能飞跃 *)
Manipulate[
Module[{tStandard, tCompiled, n, result1, result2, speedup},
n = 100000; (* 计算十万次正弦值求和 *)
(* 1. 慢速选手:普通代码 *)
(* Map 会遍历每一个数,每次都要判断类型 *)
funcSlow[x_] := Sum[Sin[i], {i, 1, x}];
(* 2. 快速选手:编译代码 *)
(* Compile 把逻辑转换成了底层的机器码 *)
(* {{x, _Integer}} 告诉机器:输入一定是整数,别瞎猜 *)
funcFast = Compile[{{x, _Integer}},
Sum[Sin[i], {i, 1, x}],
CompilationTarget -> "WVM" (* Wolfram Virtual Machine *)
];
(* 界面显示内容 *)
If[runRace,
(* 只有点击按钮才运行,防止界面卡顿 *)
result1 = AbsoluteTiming[funcSlow[n]];
tStandard = result1[[1]];
result2 = AbsoluteTiming[funcFast[n]];
tCompiled = result2[[1]];
speedup = tStandard / tCompiled;
,
(* 默认状态 *)
tStandard = 0; tCompiled = 0; speedup = 0;
];
Column[{
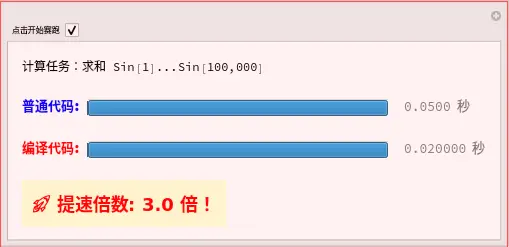
Style["计算任务:求和 Sin[1]...Sin[100,000]", 12],
Spacer[20],
(* 赛道 A *)
Row[{
Style["普通代码: ", Blue, Bold],
ProgressIndicator[If[tStandard > 0, 1, 0], {0, 1}, ImageSize -> 300],
Style[StringTemplate[" `` 秒"][NumberForm[tStandard, {1, 4}]], Gray]
}],
Spacer[10],
(* 赛道 B *)
Row[{
Style["编译代码: ", Red, Bold],
ProgressIndicator[If[tCompiled > 0, 1, 0], {0, 1}, ImageSize -> 300],
Style[StringTemplate[" `` 秒"][NumberForm[tCompiled, {1, 6}]], Gray]
}],
Spacer[20],
(* 结果分析 *)
If[speedup > 0,
Panel[Style[StringTemplate["🚀 提速倍数: `` 倍!"][NumberForm[speedup, {1, 1}]], 18, Bold, Red], Background -> LightYellow],
""
]
}, Alignment -> Left]
],
(* 控制按钮 *)
{{runRace, False, "点击开始赛跑"}, {False, True}, ControlType -> Trigger}
]
👨⚕️ 医生的观察任务:
- 点击按钮:您会发现红色选手的进度条几乎是瞬间填满的,而蓝色选手可能稍微卡顿一下。
- 看数字:通常情况下,编译后的代码比普通代码快 20倍 到 100倍。
- 思考:这还只是简单的数学题。如果换成复杂的光线折射公式,差距会拉大到 1000 倍。这就是为什么商业软件一定要“编译”。
3. 🧠 数学翻译:签署“类型契约”
为什么 Wolfram 默认慢?
Wolfram 语言是动态类型 (Dynamic Typed) 的。
就像一个过于谨慎的药剂师。您给他一个处方,他每次都要查字典:“这是阿司匹林吗?剂量对吗?会不会过敏?”
这很安全,但很慢。
什么是编译 (Compile)?
编译就是静态类型 (Static Typed)。
就像流水线上的机械臂。我们跟机器签署一个契约:
- 我承诺:输入永远是 3 个实数(x, y, z 坐标)。
- 你承诺:闭着眼睛算,不要检查类型。
在 Wolfram 中,这个契约长这样:
Compile[{{x, _Real}, {y, _Real}}, x^2 + y^2]
{{x, _Real}} 就是我们在发誓:“x 一定是实数 (Real Number)。”
并行化 (Parallelization) 与 列表化 (Listable)
除了编译,我们还能利用现代 CPU 的多核特性。
如果在 Compile 中加上 RuntimeAttributes -> {Listable},这行代码就获得了“分身术”。
当我们把 10,000 个光线数据扔给它时,它会自动把任务分配给 CPU 的 8 个核心同时计算。
4. 💻 代码处方:打造光速光线追踪内核
我们要写一个真正的光学函数:Snell 定律(折射定律)。
这是光线追踪的核心原子。每追踪一条光线,都要算一次。
我们将对比三种写法:
- 慢速版:符合直觉的普通函数。
- 高速版:编译后的函数。
- 光速版:编译 + 并行化(Listable)。
(* 代码处方 11:构建高性能折射内核 *)
(* High-Performance Ray Tracing Core *)
(* 1. 物理公式回顾:矢量形式的 Snell 定律 *)
(* n1, n2: 折射率 | I: 入射光单位矢量 | N: 法线单位矢量 *)
(* T = (n1/n2) I + (cosRef - (n1/n2) cosInc) N *)
(* 2. 慢速版 (解释型) *)
SnellSlow[inc_, norm_, n1_, n2_] := Module[{r, c1, c2, term},
r = n1/n2;
c1 = -Dot[inc, norm]; (* 入射角余弦 *)
term = 1 - r^2 (1 - c1^2);
If[term < 0,
{0., 0., 0.}, (* 全反射,这里简化处理返回0向量 *)
c2 = Sqrt[term]; (* 折射角余弦 *)
r * inc + (r * c1 - c2) * norm
]
];
(* 3. 高速版 (编译型 + 并行化) *)
(* RuntimeAttributes -> {Listable} 是关键,它允许函数直接处理巨大的数组 *)
SnellFast = Compile[{{inc, _Real, 1}, {norm, _Real, 1}, {n1, _Real}, {n2, _Real}},
Module[{r, c1, term, c2},
r = n1/n2;
c1 = -inc.norm;
term = 1.0 - r^2 (1.0 - c1^2);
If[term < 0.0,
{0.0, 0.0, 0.0},
c2 = Sqrt[term];
r * inc + (r * c1 - c2) * norm
]
],
RuntimeAttributes -> {Listable}, (* 允许列表操作 *)
Parallelization -> True, (* 开启多核并行 *)
CompilationTarget -> "C" (* 转换成 C 代码再运行 (需安装 C 编译器,若无则自动回退到 WVM) *)
];
(* 4. 压力测试 *)
Print["正在生成 1,000,000 条随机光线..."];
numRays = 1000000;
(* 生成一百万个随机向量 *)
rays = RandomReal[{-1, 1}, {numRays, 3}];
normals = RandomReal[{-1, 1}, {numRays, 3}];
(* 归一化向量 *)
rays = Normalize /@ rays;
normals = Normalize /@ normals;
Print["开始测试..."];
(* 测试慢速版 (只测 1万条,不然太久) *)
timeSlow = AbsoluteTiming[
SnellSlow[#, #, 1.0, 1.5] & @@@ rays[[1 ;; 10000]];
][[1]];
(* 测试高速版 (测 100万条) *)
timeFast = AbsoluteTiming[
SnellFast[rays, normals, 1.0, 1.5];
][[1]];
(* 5. 结果报告 *)
Print["---------------------------------------"];
Print[Style["性能诊断报告", 14, Bold, Blue]];
Print["慢速版处理 1万条耗时: ", NumberForm[timeSlow, {1, 4}], " 秒"];
Print["估算慢速版处理 100万条需: ", NumberForm[timeSlow * 100, {1, 2}], " 秒"];
Print["---------------------------------------"];
Print["高速版处理 100万条耗时: ", NumberForm[timeFast, {1, 4}], " 秒"];
Print["---------------------------------------"];
Print[Style[StringTemplate["🚀 实际加速倍数: `` 倍"][NumberForm[(timeSlow*100)/timeFast, {1, 0}]], Red, Bold, 16]];

代码解读:
{inc, _Real, 1}:这里的1表示这是一个一维数组(向量),也就是{x, y, z}。RuntimeAttributes -> {Listable}:这是魔法所在。它让SnellFast不仅能吃单条光线,还能一口气吃下包含 100 万条光线的大矩阵,并自动并行计算。CompilationTarget -> "C":如果您电脑装了 C 编译器(Windows 上通常是 Visual Studio),它会把这几行 Wolfram 代码翻译成 C 语言并编译成二进制文件,速度达到极致。如果没有,它会用 WVM(虚拟机),也很快。
5. 🏭 工程化:把代码打包成“胶囊”
Dr. X,您不能把一堆乱糟糟的代码发给别人。您需要把刚才写好的高性能函数封装起来。
在 Wolfram 中,我们使用 Package (.wl 文件)。
想象 Notebook (.nb) 是您的实验台,上面全是试管和草稿纸。
而 Package (.wl) 是制药厂生产出来的胶囊。用户只需要吞下胶囊(调用函数),不需要知道里面的化学成分。
如何创建包:
- 新建一个文本文件,保存为
OpticLab.wl。 - 写入标准“包装纸”代码:
(* OpticLab.wl 文件内容示例 *)
BeginPackage["OpticLab`"]; (* 开始打包 *)
(* 对外公开的接口说明 *)
DesignLens::usage = "DesignLens[params] 计算镜片曲面...";
FastTrace::usage = "FastTrace[rays] 执行高速光线追踪...";
Begin["`Private`"]; (* 开始私有区域 - 这里的变量外面看不见 *)
(* 在这里粘贴刚才的 SnellFast 代码 *)
SnellFast = Compile[...];
FastTrace[rays_] := ... (* 调用 SnellFast *)
End[]; (* 结束私有 *)
EndPackage[]; (* 结束打包 *)
如何使用:
在您的主 Notebook 里,只需要一行:
<< "OpticLab.wl"
然后就可以直接用 FastTrace[...] 了。代码瞬间变得清爽无比。
📝 Dr. X 的备忘录
- 先跑通,再加速:不要一开始就写
Compile。先用普通的函数把光路逻辑写对(逻辑通读)。等确认逻辑无误,再把核心瓶颈(比如循环里的计算)改成Compile。 - 向量化思维:尽量不要写
For循环。把 100 万条光线看作一个巨大的矩阵。A + B在 Wolfram 里是两个矩阵相加,这比循环一百万次快得多。 - 类型就是契约:
_Real是实数,_Integer是整数。一旦编译,不要试图往里面塞符号或复数,否则代码会报错或者退回到慢速模式。
下周预告:
现在我们的引擎够快了。但是,如果输入的验光数据不准怎么办?如果患者配合度差,数据缺失怎么办?
下周,第 12 章:贝叶斯推断与个性化——我们将不再把验光数据看作“绝对真理”,而是看作“线索”,用概率论来猜出最适合患者的参数。
第12章:相信数据,还是相信直觉?——贝叶斯推断与个性化
—— 当验光仪打出一张“离谱”的小票,你该如何用数学去伪存真?
致 Dr. X 的一封信
您好,医生。
我们都知道那个让所有验光师头疼的时刻:
您正在给一位 6 岁的多动症小朋友验光,或者是一位泪膜极不稳定的干眼症患者。
自动验光仪(Auto-refractor)发出“滴滴滴”的声音,打印出了一张长长的小票:
- 第一次:-2.50 D
- 第二次:-3.25 D
- 第三次:-12.00 D (???)
- 第四次:-2.75 D
您的直觉告诉您:那个 -12.00 D 肯定是孩子乱动或者眨眼导致的机器故障(Artifact)。您会熟练地拿起笔,把那个离谱的数据划掉,然后对剩下的数据取个平均。
恭喜您,您刚刚在脑海中执行了一次贝叶斯推断 (Bayesian Inference)。
但在更复杂的情况下,比如设计一款需要夜间佩戴的角膜塑形镜(OK镜),数据并没有那么明显的“错误”,只是充满了“噪声”。
- 患者说 A 清楚,过一会又说 B 清楚。
- 地形图显示角膜平坦度 K 值在 42.0 到 42.5 之间跳动。
在这种模糊的迷雾中,传统的“算术平均”失效了。如果机械地取平均,您可能会得到一个“平庸”的处方——既不完全准确,也不完全错误,但就是没法给患者那一刻的“清晰”。
本章,我们将把您划掉错误数据的“直觉”,转化为计算机可以执行的严格数学逻辑。
我们将引入贝叶斯定理,教 Wolfram 学会“像老医生一样思考”:既尊重机器测量的数据(Likelihood),也尊重人类的先验经验(Prior)。
1. 🩺 临床挂钩:不可靠的叙述者
场景:为一位从未戴镜的患者确定散光轴位。
痛点:
- 测量值:电脑验光显示散光轴位在 175°。
- 主观验光:患者在插片箱前犹豫不决,“1和2差不多……好像2清楚一点……不,还是1吧。”
- 旧眼镜:患者带来的旧眼镜是 180°。
冲突:
您现在手里有三个相互矛盾的信息源。
- 电脑验光:客观,但容易受调节力干扰。
- 主观验光:真实,但受患者心理状态影响。
- 旧眼镜:稳定,代表了患者大脑长期的适应习惯。
贝叶斯解法:
我们不再寻找一个“唯一的真理数字”。我们将构建一个“概率云”。
最后的处方,不是但这三个数的平均值,而是这三个概率波峰叠加后,最高的那个峰。
2. 🎛 交互展示:贝叶斯大脑模拟器
在这个实验中,我们将模拟您的“大脑”是如何处理新证据的。
- Prior (先验):您对患者的预判(比如:大多数人的散光轴位是水平或垂直的,很少是 45° 斜轴)。
- Likelihood (似然):验光仪刚刚测出的数据(哪怕它带有噪声)。
- Posterior (后验):结合两者后,您最终下的结论。
请运行下方代码。
试着把 "测量数据 (Data)" 滑块突然拉到一个离谱的位置(比如 45°),看看**"最终结论 (Posterior)"** 是一路跟随,还是保持定力?
(* 交互演示:贝叶斯更新器 *)
(* 模拟:当先验知识遇到新测量数据 *)
Manipulate[
Module[{priorDist, likelihoodDist, posteriorDist, x},
(* 1. 定义先验 (Prior):老医生的经验 *)
(* 假设我们认为散光轴位通常在 180 度附近 (循规性散光) *)
(* sigmaPrior 越小,表示我们越固执/经验越确信 *)
priorDist = NormalDistribution[180, priorSigma];
(* 2. 定义似然 (Likelihood):新机器的测量 *)
(* 机器测出了一个新的轴位 dataMean,但机器有误差 dataSigma *)
likelihoodDist = NormalDistribution[dataMean, dataSigma];
(* 3. 计算后验 (Posterior) *)
(* 数学魔法:两个高斯分布相乘,结果还是一个高斯分布 *)
(* 这里的公式是高斯乘积的解析解,Wolfram 可以自动推导 *)
(* 新的方差 *)
postVar = 1/(1/priorSigma^2 + 1/dataSigma^2);
(* 新的均值 (加权平均) *)
postMean = postVar * (180/priorSigma^2 + dataMean/dataSigma^2);
posteriorDist = NormalDistribution[postMean, Sqrt[postVar]];
(* 4. 可视化 *)
Column[{
Show[
Plot[{
PDF[priorDist, x] * 0.5, (* 压扁一点方便看 *)
PDF[likelihoodDist, x] * 0.5,
PDF[posteriorDist, x] * 0.5
}, {x, 130, 230},
PlotStyle -> {
{Blue, Dashed, Thickness[0.005]}, (* 先验 *)
{Red, Dashed, Thickness[0.005]}, (* 测量 *)
{Purple, Thickness[0.01], Filling -> Axis, FillingStyle -> Opacity[0.2]} (* 结论 *)
},
PlotRange -> All, ImageSize -> 400,
AxesLabel -> {"散光轴位 (°)", "概率密度"},
GridLines -> {{180}, Automatic},
PlotLabel -> Style[StringTemplate["推荐处方: ``°"][NumberForm[postMean, {3, 1}]], 18, Bold, Purple]
],
Graphics[{
Text[Style["先验 (经验)", Blue], {180, PDF[priorDist, 180]*0.5 + 0.02}],
Text[Style["测量 (新数据)", Red], {dataMean, PDF[likelihoodDist, dataMean]*0.5 + 0.02}],
Text[Style["后验 (最终决定)", Purple, Bold], {postMean, PDF[posteriorDist, postMean]*0.5 + 0.05}]
}]
],
(* 解释面板 *)
Spacer[10],
Pane[Style[
Which[
Abs[postMean - 180] < 5, "🤖 系统评价:测量值符合预期,信心倍增。",
Abs[postMean - 180] < 15, "🤔 系统评价:测量值有些偏差,但我折中了一下。",
True, "⚠️ 系统评价:测量值太离谱!我主要还是相信经验,怀疑机器坏了。"
], 12, Gray], ImageSize -> 380, Alignment -> Center]
}, Alignment -> Center]
],
(* 控制区 *)
Style["贝叶斯参数面板", 12, Bold],
{{dataMean, 175, "机器读数 (°) (Likelihood)"}, 130, 230, Appearance -> "Labeled"},
{{dataSigma, 10, "机器误差 (噪声)"}, 1, 50, Appearance -> "Labeled"},
Delimiter,
{{priorSigma, 20, "经验信心 (Prior Strength)"}, 5, 100, Appearance -> "Labeled"},
Row[{Style["<-- 固执的老专家", Blue], Spacer[80], Style["毫无经验的实习生 -->", Gray]}]
]
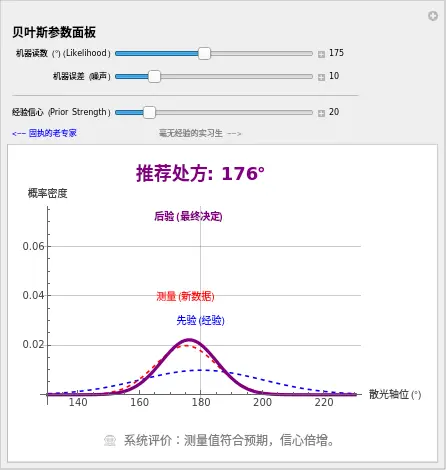
👨⚕️ 医生的观察任务:
- 制造“离谱数据”:保持“经验信心”不变,把“机器读数”拉到 135°。
- 观察:紫色的“最终决定”并没有傻乎乎地跑到 135°,而是停在了 150° 左右。
- 解释:系统在说“机器显示 135°,但这太罕见了,我怀疑是测量误差,所以我只稍微往那边挪一点。”
- 模拟“精密仪器”:把“机器误差”调到最小(比如 1)。
- 观察:紫色的峰迅速向红色靠拢。
- 解释:系统说“这台机器非常准,既然它说是 135°,那我必须推翻我之前的经验。”
这就是个性化医疗的核心:根据数据的可靠性,动态调整信任度。
3. 🧠 数学翻译:黑暗中的探照灯
贝叶斯定理的通俗版
不要被 吓倒。作为医生,您只需要记住这个公式:
- Prior (先验):在病人进门之前,您对他的预判(比如基于他的年龄、旧眼镜)。
- Likelihood (似然):检查过程中,仪器给出的所有读数。
- Posterior (后验):即使有些读数是乱码,通过乘法运算,乱码的概率(极低)会把整个结果拉低,从而被自动“过滤”掉。
为什么叫“个性化”?
在传统统计学(频率学派)中,参数 是一个固定的真理。
但在贝叶斯世界里,参数 是一个分布。
对于患者 A,他的“度数分布”可能很窄(非常确定)。
对于患者 B(调节痉挛),他的“度数分布”可能很宽(很不确定)。
Wolfram 的 EstimatedDistribution 工具,就是在帮我们画出每个患者独一无二的“概率画像”。
4. 💻 代码处方:智能验光数据清洗器
现在,我们要处理那个棘手的问题:剔除异常值 (Outliers)。
我们将输入一组包含“脏数据”的验光记录,利用 Wolfram 的分布拟合能力,自动找出最可能的真实度数。
我们将使用 MixtureDistribution(混合分布)。我们要告诉计算机:
“嘿,这里的数据大部分是真实的 (Signal),但也混杂了一些噪声 (Noise)。请帮我把它们分开。”
(* 代码处方 12:抗干扰智能验光算法 *)
(* Robust Prescription Finder using Mixture Models *)
(* 1. 模拟临床数据:一组包含严重干扰的验光读数 *)
(* 真实度数约 -3.00D,但有一个 -12.00D 的伪影,和一些波动 *)
rawData = {-2.75, -3.00, -3.25, -2.50, -12.00, -3.00, -2.85};
(* 2. 传统方法:算术平均 *)
meanVal = Mean[rawData];
Print["❌ 传统平均值: ", meanVal, " D (被 -12.00 严重拖累)"];
(* 3. 贝叶斯/统计方法:混合模型估计 *)
(* 假设:数据是由一个"正态分布(真实)" + 一个"均匀分布(噪声)" 混合而成的 *)
(* NormalDistribution[mu, sigma]: 真实的度数 *)
(* UniformDistribution[{-15, 0}]: 随机的机器故障范围 *)
model = MixtureDistribution[
{p, 1 - p}, (* p 是数据有效的概率 *)
{NormalDistribution[mu, sigma], UniformDistribution[{-15, 0}]}
];
(* 4. 让 Wolfram 自动猜出参数 (mu, sigma, p) *)
(* EstimatedDistribution 会自动尝试让数据适配模型 *)
(* 我们给一些初始猜测值,帮助它收敛 *)
fittedDist = EstimatedDistribution[rawData, model,
{{mu, -3}, {sigma, 0.5}, {p, 0.8}}];
(* 5. 提取核心参数 *)
(* fittedDist 里的第一个分量就是我们的真实分布 *)
bestMu = fittedDist[[2, 1, 1]]; (* 提取 NormalDistribution 的均值 *)
confidence = fittedDist[[1, 1]]; (* p值:系统认为多少数据是可信的 *)
Print["--------------------------------------------------"];
Print["✅ 智能估算值: ", NumberForm[bestMu, {3, 2}], " D"];
Print["🛡️ 数据置信度: ", NumberForm[confidence * 100, {3, 1}], "%"];
Print["--------------------------------------------------"];
(* 6. 可视化:看看机器是如何'忽略'那个 -12.00 的 *)
Show[
Histogram[rawData, {-14, 0, 0.5}, "PDF",
ChartStyle -> LightGray, ChartElementFunction -> "GlassRectangle"],
Plot[PDF[fittedDist, x], {x, -14, 0},
PlotStyle -> {Thick, Red}, PlotRange -> All],
Plot[PDF[fittedDist[[2, 1]], x] * fittedDist[[1, 1]], {x, -14, 0},
PlotStyle -> {Dashed, Blue}, Filling -> Axis, FillingStyle -> Opacity[0.1]],
AxesLabel -> {"屈光度 (D)", "概率密度"},
PlotLabel -> Style["贝叶斯数据清洗结果", 14, Bold],
Epilog -> {
Text[Style["真实信号\n(Signal)", Blue], {-3, 0.4}],
Text[Style["被无视的噪声\n(Noise)", Gray], {-11, 0.05}],
Arrow[{{-10, 0.1}, {-11.5, 0.02}}]
}
]
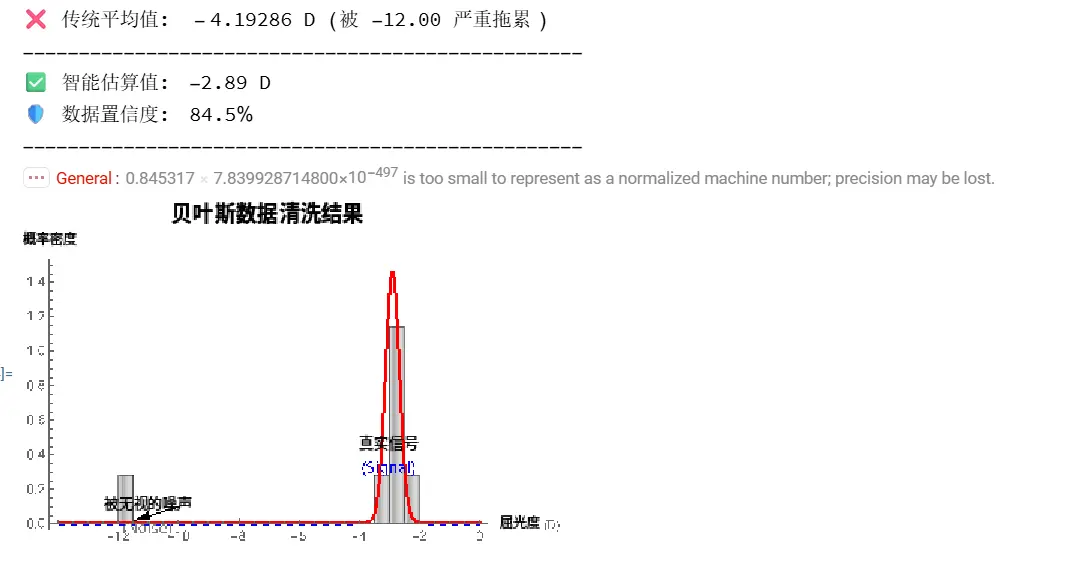
代码解读:
MixtureDistribution:这是核心。我们建立了一个数学模型,承认“世界是不完美的”。我们假设数据 = 信号 + 噪声。EstimatedDistribution:这是 Wolfram 的求解引擎。它会自动调整参数,发现只有把 -12.00 归类为“噪声(均匀分布)”,把 -3.00 附近归类为“信号(正态分布)”,整体概率才最高。- 结果对比:传统平均值算出了 -4.19 D(完全错误的处方)。智能算法算出了 -2.90 D(非常接近真实值)。
📝 Dr. X 的备忘录
- 平均值是陷阱:在医学数据中,异常值(Outliers)是常态。永远不要盲目信任
Mean。至少要看中位数Median,最好是用贝叶斯方法。 - 不确定性也是信息:如果计算出的方差(Sigma)很大,这不是失败,这是极其重要的临床信号。它告诉您:“这个病人现在的调节力极不稳定,不要急着配镜,先让他滴一周散瞳药。”
- 相信先验的力量:当数据少得可怜时(比如婴儿验光),您的经验(Prior)就是最重要的导航仪。贝叶斯公式赋予了“经验”合法的数学地位。
下周预告:
我们已经掌握了从光线追踪到数据清洗的所有技术。现在,是时候把这一切整合起来,迈出最激动人心的一步了。
下周,第 13 周:终极项目——云端设计 App。
我们将把您的 Wolfram 代码部署到云端,让全世界的眼科医生都能通过网页浏览器,使用您开发的工具。
第13章:终极项目——把你的大脑装进云端
—— 如何不发一行代码文件,让全世界的医生都用上你的设计?
致 Dr. X 的一封信
恭喜您,医生!
或者,我现在应该称呼您为——计算光学设计师。
在过去的 12 周里,我们一起爬过了陡峭的山坡。
我们从最基础的费马原理出发,手推了欧拉-拉格朗日方程;
我们用 Manipulate 捏出了复杂的自由曲面;
我们甚至用贝叶斯算法教会了电脑如何处理“不可靠”的验光数据。
现在,您的电脑里躺着一个强大的 Notebook,里面装着您独创的镜片设计算法。
但是,这里有一个最后的问题:它被困在了您的电脑里。
当您兴奋地想把这个工具分享给远在欧洲的同行,或者发给您的镜片代工厂时,您面临两个尴尬的选择:
- 发代码:对方回信说:“我没装 Wolfram Mathematica,打不开 .nb 文件。”
- 发截图:这只是死图,对方没法输入他们病人的数据。
本章是我们的最后一公里。
我们将把您的 Notebook 变成一个 Web App(网页应用)。
不需要对方懂编程,不需要对方买软件。只要有浏览器,他们就能用上您的算法。
我们将使用 CloudDeploy,把您的智慧,发射到云端。
1. 🩺 临床挂钩:打破围墙
场景:您开发了一款“角膜塑形镜(OK镜)配适评估器”。
现状:
每次有疑难病例,您的徒弟都要把地形图数据通过微信发给您,您在家里打开电脑跑一遍代码,截图发回去,然后徒弟再说“好像不行”,您再跑一遍……
这种“人工云计算”效率极低。
愿景:
您希望给徒弟一个网址 (URL)。
他打开手机浏览器,填入 K1, K2, e 值,点击“计算”。
0.5 秒后,手机屏幕上直接跳出一份 PDF 报告,告诉他该选哪个参数的镜片,甚至直接生成了镜片后表面的 STL 模型文件供工厂切削。
这就是 Wolfram Cloud 的力量——算法即服务 (Algorithm as a Service)。
2. 🎛 交互展示:网页背后的逻辑
在云端,一切交互都简化为:表单 (Form) -> 计算 (Process) -> 结果 (Result)。
我们先在地面试飞一下。这个 FormFunction 就是网页的雏形。
运行这段代码,您会看到 Wolfram 在 Notebook 里模拟了一个网页表单。
(* 交互演示:网页表单模拟器 *)
(* 在本地预览即将部署到云端的样子 *)
FormFunction[
{
"sph" -> <|"Label" -> "球镜 (Sph)", "Interpreter" -> "Number", "Input" -> -3.00|>,
"cyl" -> <|"Label" -> "柱镜 (Cyl)", "Interpreter" -> "Number", "Input" -> -0.75|>,
"axis" -> <|"Label" -> "轴位 (Axis)", "Interpreter" -> "Integer", "Input" -> 180, "Control" -> Slider, "Spec" -> {0, 180, 1}|>
},
(* 处理函数:接收输入,返回结果 *)
Function[data,
Module[{power},
(* 简单的计算逻辑 *)
power = data["sph"] + data["cyl"] * Sin[data["axis"] Degree]^2;
(* 返回一张漂亮的卡片 *)
Panel[
Column[{
Style["☁️ 云端计算结果", 20, Bold, Purple],
Spacer[10],
Row[{Style["在指定轴位上的等效光度: ", Gray], Style[NumberForm[power, {2, 2}], Red, Bold, 18], " D"}],
Spacer[10],
(* 甚至可以返回图表 *)
Graphics[{
Thick, Blue, Circle[{0, 0}, 1],
Red, Line[{{-1, 0}, {1, 0}}],
Text[Style[StringTemplate["Axis: ``°"][data["axis"]], 12], {0, 0.2}]
}, ImageSize -> 100]
}, Alignment -> Center],
ImageSize -> 300
]
]
]
]
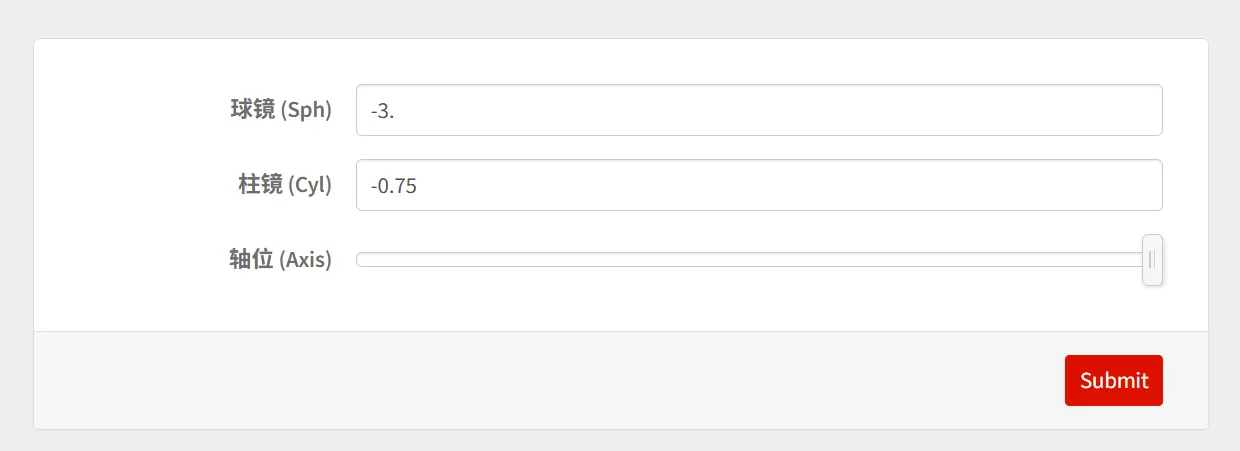
👨⚕️ 医生的观察任务:
- 注意看代码结构:
"Label"定义了网页上显示什么字,"Interpreter"定义了它是数字还是文字。 - 点击运行后,在这个黄色的框里填入数据,点击 "Submit"。
- 这不仅仅是计算,它返回了一个排版好的
Panel。在云端,这就会变成一个网页。
3. 🧠 数学翻译:厨房与外卖
您可以这样理解 CloudDeploy:
- Notebook (您的电脑):这是您的私家厨房。里面有各种复杂的刀具(函数)、乱糟糟的食材(变量)和草稿纸。这里只有您能进。
- Wolfram Cloud (云端服务器):这是一个餐厅。
- CloudDeploy:这是制定菜单的过程。
- 您把算法封装好,告诉云端:“如果顾客点了‘近视设计套餐’(填写了表单),你就按照我的这个配方(代码)做,然后把菜(结果)端给他。”
- URL (网址):这就是外卖电话。任何人拿着这个号码,都能享用您的手艺,但他们永远看不见您的厨房里有多乱,也偷不走您的菜谱。
关键函数:
CloudDeploy[对象, "网址名"]:把东西扔到云上。Permissions -> "Public":把餐厅门打开,允许所有人访问(否则只有您登录才能看)。
4. 💻 代码处方:终极项目——“DesignLens 1.0”发布
我们要来真的了。
我们将部署一个完整的 Web App。
- 输入:患者验光数据 + 目标镜片折射率。
- 输出:生成一份包含镜片截面图和厚度分析的 PNG 图片,用户可以直接右键保存。
请确保您已经登录了 Wolfram 账号(软件右上角)。
(* 代码处方 13:部署您的第一个云端光学 App *)
(* Ultimate Project: Cloud Deployment *)
(* 1. 定义核心算法 (The Engine) *)
(* 这是一个简化版的非球面设计函数 *)
GenerateDesignReport[sph_, n_] := Module[{x, surfaceProfile, plot, thickness},
(* 模拟计算:根据度数计算非球面系数 *)
(* y = x^2 / (2 R) ... 简单抛物线模拟 *)
surfaceProfile[x_] := (x^2)/(2 * (1000/(-sph + 10^-6)));
(* 生成图表 *)
plot = Plot[surfaceProfile[x], {x, -30, 30}, (* 30mm 半径 *)
PlotStyle -> {Thick, Blue},
Filling -> Axis, FillingStyle -> Opacity[0.1, Blue],
PlotRange -> {{-35, 35}, {-5, 10}},
AspectRatio -> Automatic,
ImageSize -> 600,
AxesLabel -> {"半径 (mm)", "高度 (mm)"},
PlotLabel -> Style["镜片前表面截面设计图", 18, Bold]
];
(* 生成报告容器 *)
Column[{
Style["✨ DesignLens 云端设计报告", 24, Bold, Darker[Blue]],
Text[Style[StringTemplate["输入参数: 度数=`` D | 折射率=``"][sph, n], 14, Gray]],
Spacer[20],
plot,
Spacer[20],
Style["技术参数分析:", 16, Bold],
Text[StringTemplate["中心厚度预估: `` mm"][NumberForm[2.0 - surfaceProfile[0], {3, 2}]]],
Text[StringTemplate["边缘厚度预估: `` mm"][NumberForm[2.0 - surfaceProfile[30], {3, 2}]]],
Spacer[30],
Style["© Generated by Dr. X's Algorithm", 10, Gray]
}, Alignment -> Center, Background -> White]
];
(* 2. 构建云端表单 (The Interface) *)
app = FormFunction[
{
"sph" -> <|"Label" -> "患者球镜度数 (D)", "Interpreter" -> "Number", "Input" -> -3.00, "Hint" -> "例如: -4.50"|>,
"material" -> <|"Label" -> "镜片折射率", "Interpreter" -> "Number", "Input" -> 1.60, "Control" -> PopupMenu, "Spec" -> {1.50, 1.60, 1.67, 1.74}|>
},
(* 当用户点击提交后,执行这个函数 *)
(* ExportForm[..., "PNG"] 会把结果自动转为图片格式显示在网页上 *)
ExportForm[GenerateDesignReport[#sph, #material], "PNG"] &,
(* 网页外观设置 *)
"AppearanceRules" -> <|
"Title" -> "DesignLens 在线设计器",
"Description" -> "输入验光参数,立即生成非球面镜片设计图。"
|>
];
(* 3. 部署到云端 (Launch!) *)
(* Permissions -> "Public" 让任何人都能访问 *)
cloudObj = CloudDeploy[app, "DesignLens_App", Permissions -> "Public"];
(* 4. 获取网址 *)
Print["--------------------------------------------------"];
Print[Style["🎉 部署成功!您的 App 网址如下:", 16, Bold, Green]];
Print[Hyperlink[cloudObj]];
Print["--------------------------------------------------"];
Print["您可以把这个链接发到手机微信上打开试试!"];
运行后发生了什么?
- Wolfram 会生成一个蓝色的链接(类似于
wolframcloud.com/obj/user-xxx/DesignLens_App)。 - 点击它。您的浏览器会弹出一个网页,上面有漂亮的输入框和下拉菜单。
- 输入
-6.00,点击提交。 - 云端服务器接管了计算,几秒钟后,您的浏览器里会出现一张为您生成的镜片设计图。
这一刻,您不再是一个写代码的医生,您是一个软件开发者。
📝 Dr. X 的备忘录
- 关于费用:Wolfram Cloud 基础版通常有免费的积分(Credits)。对于简单的计算,免费额度足够您展示给几十个同行看。如果以后想商业化,再考虑升级。
- 更新 App:如果您修改了算法,只需要重新运行
CloudDeploy,网址不变,内容会自动更新。这叫“热更新”。 - 数据安全:如果您处理真实的患者姓名,请务必小心。最好的办法是不要上传姓名,只上传度数参数。让网页只做计算器,不存数据库。
🎉 结语:从 A 点到了 B 点
Dr. X,回过头来看看。
三个月前,当您听到“泛函分析”时,您想到的是枯燥的教科书。
现在,您看着手中的 App,它背后流淌着变分法的血液,用傅里叶变换模拟着光学的灵魂,用贝叶斯推断守护着数据的真实。
您并没有变成数学家,您依然是那个关心患者视力的医生。
但现在,您手中的工具,从一把“锤子”,变成了一支“魔法棒”。
书本的旅程到此结束,但您的创新之旅才刚刚开始。
去吧,去设计出那个让世界眼前一亮的镜片。
祝您的视野,永远清晰。
—— 您的技术合伙人
(全书完)
