Gemini解读,仅供科普参考。预设读者为大一数学水平。注意这种解读不能代表DeepSeek论文的原意。
当深度学习遇见线性代数:如何用“正交矩阵”驯服深度学习巨兽?
——解读 DeepSeek 最新论文《mHC: Manifold-Constrained Hyper-Connections》 https://arxiv.org/abs/2512.24880
如果你正在大一苦读《线性代数》,面对一堆矩阵乘法、秩、特征值和正交变换感到头秃,你可能会问:“这玩意儿到底有啥用?以后买菜又用不到。”
答案来了:它能用来拯救大模型的命。
2025 年末,DeepSeek 团队发布了一项名为 mHC 的技术。这项技术的核心,不是什么玄学的魔法,而是我们线性代数课本里一个极其性感的概念——正交矩阵(Orthogonal Matrix)。
今天我们就用大一的数学知识,来看看数学家是如何给 AI 戴上“紧箍咒”的。
第一幕:从“自助餐”到“调音台”
要理解这个新技术,我们先得看看大模型是怎么传递信息的。
1. 传统的残差连接(ResNet):像吃自助餐
现在的 AI(比如 Transformer)之所以能堆到几百层,靠的是残差连接。
公式很简单:
写成矩阵形式就是:
这里有一个老朋友:单位矩阵 。
这就像吃自助餐,盘子里是原来的饭(),再给你加一勺新菜()。原来的饭还在那里,原封不动。
- 优点:稳。不管新菜多难吃,原来的饭至少还能吃(梯度不消失)。
- 缺点:死板。你不能把饭和菜打碎了混在一起吃。红色通道的信息永远在红色通道,不会跑去绿色通道。
2. 超级连接(HC):疯狂的调音台
研究人员觉得这太浪费了。为了让模型更聪明,他们引入了 Hyper-Connections (HC)。
他们把死板的单位矩阵 ,换成了一个可学习的矩阵 。
重点来了:线代视角的 RGB 例子
假设你的输入 是一张图片的三个通道:
就像一个专业的调音台,允许这样的操作:
“我希望输出的红色通道里,不再只是原来的红色,而是包含 50% 的原红,10% 的原绿,还有 40% 的新蓝。”
用矩阵乘法表示,就是这样:
- 好处:信息被打通了!模型学会了“通感”,能组合出更复杂的特征。
- 坏处(致命):过曝与死黑
如果这个矩阵 没学好,数值稍微偏离了 1.0,后果很严重:
- 梯度爆炸(过曝 - 纯白):如果矩阵让信号每一层放大 1.1 倍,过 100 层就是 。
这就好比你给照片调色,每层都把亮度调高一点点。等到最后,所有的像素值都变成了无穷大,画面变成了一片惨白的过曝光。

- 梯度消失(死黑 - 纯黑):如果矩阵让信号每一层缩小成 0.9,过 100 层就是 。
信号越来越弱,最后所有 RGB 值都趋近于 0,画面变成了一片漆黑,信息全丢了。

第二幕:请出“正交矩阵”来救场
这就到了 DeepSeek 这篇论文(mHC)的高光时刻。
作者思考了一个问题:有没有一种矩阵,既能像调音台一样混合红绿蓝(改变方向),又绝对不会让画面过曝或死黑(不改变大小)?
翻开课本,答案呼之欲出:正交矩阵(Orthogonal Matrix)。

1. 什么是 mHC 的核心直觉?
论文提出的 mHC(流形约束),核心思想就是:
允许网络去学习那个复杂的调音矩阵 ,但是,必须强迫 永远是一个正交矩阵。
2. 正交矩阵的魔力
在大一课本里,正交矩阵 满足 。它有两个雷打不动的几何性质,完美解决了 AI 的痛点:
- 性质一:旋转(Rotation)—— 负责混合
正交变换本质上是一种旋转(或反射)。
它虽然改变了向量的方向(实现了红绿蓝信息的混合),但它不会扭曲空间。 - 性质二:保范数(Norm Preservation)—— 负责稳定
对于任意向量 ,有 。
这太重要了!这意味着,无论信号在这个网络里转了多少圈,混合了多少次,它的总能量(向量长度)永远不变。- 既不会因为能量无限放大而变成纯白过曝。
- 也不会因为能量衰减而变成纯黑死寂。
- 正交矩阵是带着脚镣跳舞,既灵活又安全。
第三幕:怎么把矩阵“按”在流形上?
这篇论文名字里的“流形”(Manifold),其实就是指所有正交矩阵构成的几何集合(Stiefel 流形)。
在训练 AI 时,梯度下降(SGD)往往会像个莽夫,一步就把矩阵 更新得不正交了(数值可能会变大)。
mHC 的做法可以形象地理解为 “投影” :
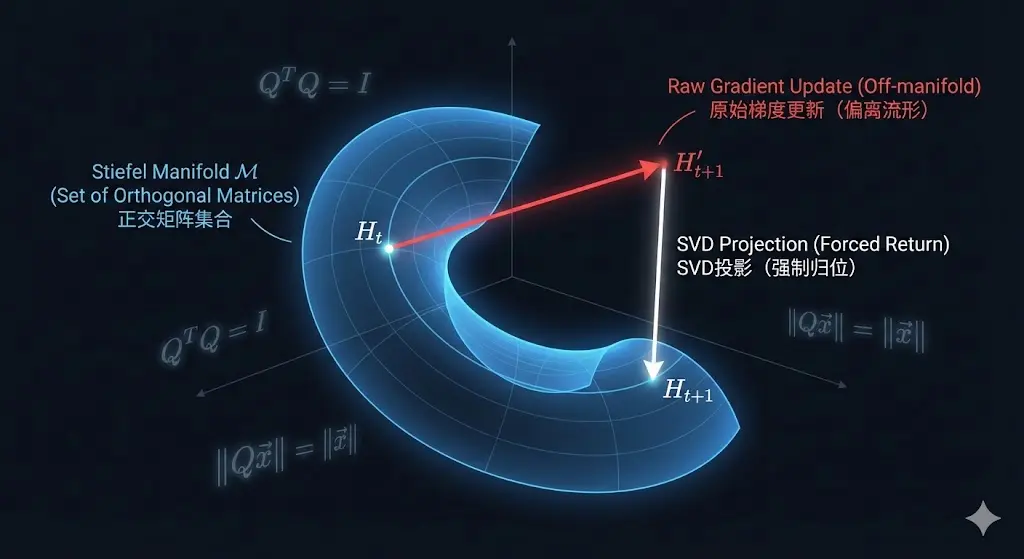
- 更新:算法计算出矩阵 该怎么变。
- 检查:诶?这一步走完,矩阵 的列向量不垂直了,长度也不是 1 了(掉出流形了)。
- 强制归位:运用数学工具(比如 SVD 分解或者 QR 分解),强行把变形的矩阵 “捏”回 正交矩阵的样子。
形象比喻:
- HC:你可以随便跑,结果你跑到了外太空(数值爆炸)。
- mHC:你想跑?可以。但我把你绑在了一个球面上。你可以在球面上随便转圈(混合信息),但你永远离不开球心(数值稳定)。
总结
所以,这篇 DeepSeek 的论文其实是给了我们一个启示:
当我们在设计最前沿的 AI 系统时,并没有用到什么天书般的魔法。最后能依靠的,依然是那几块最坚固的基石:
- 线性变换(负责混合信息)
- 范数(负责控制能量)
- 正交性(负责在混合与稳定之间找到平衡)
下一次,当你在习题集里证明 时,别把它当成枯燥的公式。请记住,正是这个等式,正在支撑着那些千亿参数的超级大脑。
演示代码
https://gemini.google.com/share/371cc6a66a17
<!DOCTYPE html>
<html lang="zh-CN">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>DeepSeek mHC: 线性代数与深度学习可视化</title>
<script src="https://cdn.tailwindcss.com"></script>
<!-- 引入 KaTeX 用于渲染 LaTeX 公式 -->
<link rel="stylesheet" href="https://cdn.jsdelivr.net/npm/[email protected]/dist/katex.min.css" xintegrity="sha384-n8MVd4RsNIU0tAv4ct0nTaAbDJwPJzDEaqSD1odI+WdtXRGWt2kTvGFasHpSy3SV" crossorigin="anonymous">
<script src="https://cdn.jsdelivr.net/npm/[email protected]/dist/katex.min.js" xintegrity="sha384-XjKyQNRlToSoW462lSSzOu3vosZxl96NSZ0hzM/lSzMjkSxQIKC+05asHgnIFh5+" crossorigin="anonymous"></script>
<script src="https://cdn.jsdelivr.net/npm/[email protected]/dist/contrib/auto-render.min.js" xintegrity="sha384-+VBxd3r6XgURycqtZ117nYw44OOcIax56Z4dCRWbxyPt0Koah1uHoK0o4+/RRE05" crossorigin="anonymous"></script>
<style>
body { font-family: 'Segoe UI', Tahoma, Geneva, Verdana, sans-serif; }
canvas { border: 1px solid #e5e7eb; box-shadow: 0 4px 6px -1px rgba(0, 0, 0, 0.1); }
/* 确保公式字体大小合适 */
.katex { font-size: 1.1em; }
</style>
</head>
<body class="bg-gray-50 text-gray-800 min-h-screen p-4 flex flex-col items-center">
<!-- 标题区 -->
<header class="text-center mb-8 max-w-3xl">
<h1 class="text-3xl font-bold text-blue-700 mb-2">DeepSeek mHC 可视化演示</h1>
<p class="text-sm text-gray-600 mb-4">基于论文《mHC: Manifold-Constrained Hyper-Connections》</p>
<div class="bg-white p-4 rounded-lg shadow-sm text-left text-sm border-l-4 border-blue-500">
<p class="mb-2"><strong>实验说明:</strong> 我们将把 RGB 像素 $(r, g, b)$ 视为三维向量 $\vec{x}$,并在每一“层”(Step)应用矩阵乘法 $\vec{x}_{new} = M \cdot \vec{x}$。</p>
<ul class="list-disc pl-5 space-y-1">
<li><span class="font-bold text-red-500">HC (普通矩阵)</span>:特征值不稳定。$>1$ 时能量无限放大(全白/爆炸),$<1$ 时能量衰减(全黑/消失)。</li>
<li><span class="font-bold text-green-600">mHC (Cayley流形变换)</span>:通过随机反对称矩阵 $S$ 构造 $Q=(I-S)(I+S)^{-1}$。模拟深层网络中每一层复杂但正交的特征混合,**能量严格守恒**。</li>
</ul>
</div>
</header>
<!-- 主控制区 -->
<main class="w-full max-w-6xl flex flex-col md:flex-row gap-6">
<!-- 左侧:设置与监控 -->
<div class="md:w-1/3 flex flex-col gap-6 order-2 md:order-1">
<!-- 模式选择 -->
<div class="bg-white p-5 rounded-xl shadow-md border-t-4 border-blue-500">
<h3 class="font-bold text-lg mb-3 border-b pb-2 flex items-center gap-2">
<span>⚙️</span> 1. 矩阵模式设置
</h3>
<div class="space-y-3">
<label class="flex items-center space-x-3 cursor-pointer p-3 hover:bg-red-50 rounded-lg border border-transparent hover:border-red-200 transition">
<input type="radio" name="matrixType" value="explode" class="form-radio text-red-600 h-5 w-5" checked>
<div>
<span class="font-bold text-red-700 block">HC: 梯度爆炸 (Explosion)</span>
<span class="text-xs text-gray-500">特征值 > 1.0 (模拟过曝/纯白)</span>
</div>
</label>
<label class="flex items-center space-x-3 cursor-pointer p-3 hover:bg-gray-100 rounded-lg border border-transparent hover:border-gray-300 transition">
<input type="radio" name="matrixType" value="vanish" class="form-radio text-gray-600 h-5 w-5">
<div>
<span class="font-bold text-gray-700 block">HC: 梯度消失 (Vanishing)</span>
<span class="text-xs text-gray-500">特征值 < 1.0 (模拟死黑/纯黑)</span>
</div>
</label>
<label class="flex items-center space-x-3 cursor-pointer p-3 hover:bg-green-50 rounded-lg border border-transparent hover:border-green-200 transition">
<input type="radio" name="matrixType" value="orthogonal" class="form-radio text-green-600 h-5 w-5">
<div>
<span class="font-bold text-green-700 block">mHC: 随机流形游走</span>
<span class="text-xs text-gray-500">Cayley 变换 $Q=(I-S)(I+S)^{-1}$ (复杂混合)</span>
</div>
</label>
</div>
</div>
<!-- 数据监控 -->
<div class="bg-white p-5 rounded-xl shadow-md flex-grow border-t-4 border-indigo-500">
<h3 class="font-bold text-lg mb-3 border-b pb-2 flex items-center gap-2">
<span>📊</span> 实时数据监控
</h3>
<div class="space-y-5 text-sm">
<div class="flex justify-between items-end">
<span class="text-gray-600">迭代层数 (Iterations):</span>
<span id="iterCount" class="font-mono font-bold text-2xl text-blue-600">0</span>
</div>
<div>
<div class="flex justify-between mb-1">
<span class="text-gray-600">图像平均能量 (Avg Norm):</span>
<span id="normVal" class="font-mono font-bold">--</span>
</div>
<!-- 能量条 -->
<div class="w-full bg-gray-200 rounded-full h-4 dark:bg-gray-300 overflow-hidden shadow-inner relative">
<div id="normBar" class="bg-blue-600 h-4 rounded-full transition-all duration-300" style="width: 50%"></div>
</div>
<p id="statusText" class="mt-2 text-xs font-medium italic text-center text-gray-500">等待开始...</p>
</div>
<div class="bg-gray-800 text-green-400 p-3 rounded-lg font-mono text-xs overflow-x-auto shadow-inner">
<div class="mb-2 text-gray-400 border-b border-gray-700 pb-1">Matrix M (Current Layer):</div>
<div id="matrixDisplay" class="leading-relaxed">
[1.00, 0.00, 0.00]<br>
[0.00, 1.00, 0.00]<br>
[0.00, 0.00, 1.00]
</div>
</div>
</div>
</div>
</div>
<!-- 右侧:画布显示与操作 -->
<div class="md:w-2/3 flex flex-col items-center bg-gray-100 p-6 rounded-xl order-1 md:order-2 border border-gray-200">
<!-- 上传区域 -->
<div class="w-full max-w-lg mb-4 flex justify-between items-center">
<h2 class="text-xl font-bold text-gray-700">图像预览</h2>
<label class="cursor-pointer bg-white text-blue-600 px-4 py-2 rounded-lg shadow-sm border border-blue-100 hover:bg-blue-50 hover:shadow transition text-sm font-semibold flex items-center gap-2">
<svg xmlns="http://www.w3.org/2000/svg" class="h-4 w-4" fill="none" viewBox="0 0 24 24" stroke="currentColor">
<path stroke-linecap="round" stroke-linejoin="round" stroke-width="2" d="M4 16v1a3 3 0 003 3h10a3 3 0 003-3v-1m-4-8l-4-4m0 0L8 8m4-4v12" />
</svg>
更换图片
<input type="file" id="uploadInput" accept="image/*" class="hidden">
</label>
</div>
<!-- Canvas -->
<div class="relative group shadow-2xl rounded-lg overflow-hidden bg-white mb-6">
<canvas id="mainCanvas" width="500" height="500" class="max-w-full h-auto block"></canvas>
<div class="absolute top-2 right-2 bg-black bg-opacity-60 backdrop-blur-sm text-white text-xs px-2 py-1 rounded pointer-events-none">
Output View
</div>
</div>
<!-- 操作按钮 -->
<div class="w-full max-w-lg bg-white p-4 rounded-xl shadow-lg border border-gray-100">
<div class="flex items-center justify-between mb-2">
<h3 class="font-bold text-gray-700">2. 执行变换操作</h3>
<span class="text-xs text-gray-400 bg-gray-100 px-2 py-1 rounded">Controls</span>
</div>
<div class="flex flex-col gap-3">
<!-- 自动播放大按钮 -->
<button id="autoBtn" class="w-full bg-indigo-600 hover:bg-indigo-700 text-white py-3 px-6 rounded-lg font-bold shadow-md hover:shadow-lg transition-all transform active:scale-95 flex justify-center items-center gap-2 text-lg">
<span id="playIcon">▶</span> 启动连续混色
</button>
<!-- 辅助按钮组 -->
<div class="grid grid-cols-2 gap-3">
<button id="stepBtn" class="bg-white border-2 border-blue-100 text-blue-700 hover:bg-blue-50 hover:border-blue-200 py-2 rounded-lg font-semibold transition flex justify-center items-center gap-1">
<span>⏭</span> 单步 (+1)
</button>
<button id="resetBtn" class="bg-white border-2 border-gray-100 text-gray-600 hover:bg-gray-50 hover:border-gray-200 hover:text-gray-800 py-2 rounded-lg font-semibold transition flex justify-center items-center gap-1">
<span>↺</span> 重置图像
</button>
</div>
</div>
</div>
<p class="mt-4 text-gray-400 text-xs text-center max-w-sm">
提示:在移动端,控制面板位于图像下方。
</p>
</div>
</main>
<script>
// --- 初始化 KaTeX 自动渲染 ---
document.addEventListener("DOMContentLoaded", function() {
renderMathInElement(document.body, {
delimiters: [
{left: '$$', right: '$$', display: true},
{left: '$', right: '$', display: false},
{left: '\\(', right: '\\)', display: false},
{left: '\\[', right: '\\]', display: true}
],
throwOnError : false
});
});
// --- 全局变量 ---
const canvas = document.getElementById('mainCanvas');
const ctx = canvas.getContext('2d', { willReadFrequently: true });
// 核心修改:增加 Float32Array 状态存储
// 仅仅依赖 Canvas 的 ImageData (Uint8) 会导致严重的量化误差累积
let floatState = null; // 存储 float32 精度的数据 [r,g,b,a, r,g,b,a, ...]
let displayData = null; // Canvas ImageData 对象
let isRunning = false;
let animationId = null;
let iteration = 0;
// 初始化浮点数状态
function initFloatState(width, height, sourceData = null) {
const len = width * height * 4;
floatState = new Float32Array(len);
if (sourceData) {
// 从现有数据(例如上传的图片)初始化
for(let i=0; i<len; i++) {
floatState[i] = sourceData[i];
}
} else {
// 生成默认数据
for (let y = 0; y < height; y++) {
for (let x = 0; x < width; x++) {
const index = (y * width + x) * 4;
floatState[index] = Math.floor((x / width) * 255); // R
floatState[index + 1] = Math.floor((y / height) * 255); // G
floatState[index + 2] = Math.floor(((width - x) / width) * 255); // B
floatState[index + 3] = 255; // Alpha
}
}
}
displayData = ctx.createImageData(width, height);
syncDisplay();
}
// 将浮点状态同步到 Canvas 显示层 (Uint8)
function syncDisplay() {
if (!floatState || !displayData) return;
const d = displayData.data;
const len = floatState.length;
for(let i=0; i<len; i++) {
// Canvas 自动 clamp 到 0-255,这里可以直接赋值
// 但为了严谨,我们通常在 float 运算中不截断,只在显示时截断
d[i] = floatState[i];
}
ctx.putImageData(displayData, 0, 0);
}
// 默认图片生成
function drawDefaultImage() {
const w = canvas.width;
const h = canvas.height;
initFloatState(w, h); // 初始化 float 状态
// 为了画文字,我们先同步一次到 canvas,用 ctx 画字,再读回来更新 floatState
// 这是一个折衷办法,为了能利用 canvas 便捷的绘图 API
syncDisplay();
ctx.fillStyle = "rgba(255, 255, 255, 0.2)";
ctx.font = "bold 80px sans-serif";
ctx.textAlign = "center";
ctx.fillText("mHC", w/2, h/2);
// 读回带文字的图像数据更新到 floatState
const tempImgData = ctx.getImageData(0, 0, w, h);
for(let i=0; i<tempImgData.data.length; i++) {
floatState[i] = tempImgData.data[i];
}
iteration = 0;
updateStats();
}
// --- 矩阵数学逻辑 ---
// 辅助函数:3x3 矩阵乘法
function matMul(A, B) {
let C = [[0,0,0],[0,0,0],[0,0,0]];
for(let i=0; i<3; i++) {
for(let j=0; j<3; j++) {
for(let k=0; k<3; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
return C;
}
// 辅助函数:3x3 矩阵求逆 (针对 I+S, S为反对称矩阵,一定可逆)
function matInv(M) {
// 计算行列式
const det = M[0][0] * (M[1][1] * M[2][2] - M[1][2] * M[2][1]) -
M[0][1] * (M[1][0] * M[2][2] - M[1][2] * M[2][0]) +
M[0][2] * (M[1][0] * M[2][1] - M[1][1] * M[2][0]);
const invDet = 1 / det;
let Res = [[0,0,0],[0,0,0],[0,0,0]];
Res[0][0] = (M[1][1] * M[2][2] - M[1][2] * M[2][1]) * invDet;
Res[0][1] = (M[0][2] * M[2][1] - M[0][1] * M[2][2]) * invDet;
Res[0][2] = (M[0][1] * M[1][2] - M[0][2] * M[1][1]) * invDet;
Res[1][0] = (M[1][2] * M[2][0] - M[1][0] * M[2][2]) * invDet;
Res[1][1] = (M[0][0] * M[2][2] - M[0][2] * M[2][0]) * invDet;
Res[1][2] = (M[1][0] * M[0][2] - M[0][0] * M[1][2]) * invDet;
Res[2][0] = (M[1][0] * M[2][1] - M[1][1] * M[2][0]) * invDet;
Res[2][1] = (M[2][0] * M[0][1] - M[0][0] * M[2][1]) * invDet;
Res[2][2] = (M[0][0] * M[1][1] - M[1][0] * M[0][1]) * invDet;
return Res;
}
// 生成矩阵
function getMatrix() {
const type = document.querySelector('input[name="matrixType"]:checked').value;
if (type === 'explode') {
return [[1.1, 0, 0], [0, 1.1, 0], [0, 0, 1.1]];
} else if (type === 'vanish') {
return [[0.9, 0, 0], [0, 0.9, 0], [0, 0, 0.9]];
} else {
// --- mHC: 随机流形游走 ---
// 1. 生成一个随机的反对称矩阵 S
const range = 0.8; // 加大一点变化幅度让效果更明显
const a = (Math.random() - 0.5) * range;
const b = (Math.random() - 0.5) * range;
const c = (Math.random() - 0.5) * range;
// S^T = -S
const S = [
[0, -c, b],
[c, 0, -a],
[-b, a, 0]
];
// Identity
const I_minus_S = [
[1, c, -b],
[-c, 1, a],
[b, -a, 1]
];
const I_plus_S = [
[1, -c, b],
[c, 1, -a],
[-b, a, 1]
];
// Q = (I - S)(I + S)^-1
const I_plus_S_inv = matInv(I_plus_S);
const Q = matMul(I_minus_S, I_plus_S_inv);
return Q;
}
}
// 应用矩阵 (现在操作的是 floatState)
function applyMatrix(matrix) {
const len = floatState.length;
let totalEnergy = 0;
let pixelCount = 0;
for (let i = 0; i < len; i += 4) {
const r = floatState[i];
const g = floatState[i + 1];
const b = floatState[i + 2];
// alpha floatState[i+3] 不变
// 矩阵乘法 (在 float32 精度下进行)
const r_new = matrix[0][0]*r + matrix[0][1]*g + matrix[0][2]*b;
const g_new = matrix[1][0]*r + matrix[1][1]*g + matrix[1][2]*b;
const b_new = matrix[2][0]*r + matrix[2][1]*g + matrix[2][2]*b;
floatState[i] = r_new;
floatState[i + 1] = g_new;
floatState[i + 2] = b_new;
// 计算能量
totalEnergy += Math.sqrt(r_new*r_new + g_new*g_new + b_new*b_new);
pixelCount++;
}
return totalEnergy / pixelCount;
}
// --- UI 更新逻辑 ---
function updateUI(matrix, avgEnergy) {
document.getElementById('iterCount').innerText = iteration;
const mStr = matrix.map(row => `[${row.map(v => v.toFixed(2).padStart(5)).join(', ')}]`).join('<br>');
document.getElementById('matrixDisplay').innerHTML = mStr;
if (avgEnergy !== null) {
document.getElementById('normVal').innerText = avgEnergy.toFixed(2);
let percent = (avgEnergy / 441) * 100;
if (percent > 100) percent = 100;
document.getElementById('normBar').style.width = `${percent}%`;
const bar = document.getElementById('normBar');
const status = document.getElementById('statusText');
if (avgEnergy > 400) {
bar.className = "h-4 rounded-full transition-all duration-300 bg-red-600";
status.innerText = "警告:能量过饱和 (梯度爆炸 / 过曝)";
status.className = "mt-2 text-xs font-bold text-center text-red-600";
} else if (avgEnergy < 10) {
bar.className = "h-4 rounded-full transition-all duration-300 bg-gray-800";
status.innerText = "警告:信号丢失 (梯度消失 / 死黑)";
status.className = "mt-2 text-xs font-bold text-center text-gray-800";
} else {
bar.className = "h-4 rounded-full transition-all duration-300 bg-green-500";
status.innerText = "正常:能量稳定 (Cayley流形约束生效)";
status.className = "mt-2 text-xs font-bold text-center text-green-600";
}
}
}
function step() {
iteration++;
const matrix = getMatrix();
// 计算新的 floatState
const avgEnergy = applyMatrix(matrix);
// 同步到 UI
syncDisplay();
updateUI(matrix, avgEnergy);
}
// 重新实现 Reset,现在需要重置 floatState
// 我们需要保存最初的 floatState 副本
let initialFloatState = null;
function saveInitialState() {
initialFloatState = new Float32Array(floatState);
}
function reset() {
if (initialFloatState) {
floatState = new Float32Array(initialFloatState);
iteration = 0;
// 计算初始能量
let total = 0;
for(let i=0; i<floatState.length; i+=4) {
total += Math.sqrt(floatState[i]**2 + floatState[i+1]**2 + floatState[i+2]**2);
}
syncDisplay();
updateUI([[1,0,0],[0,1,0],[0,0,1]], total / (canvas.width * canvas.height));
stopAuto();
}
}
function toggleAuto() {
const btn = document.getElementById('autoBtn');
const icon = document.getElementById('playIcon');
if (isRunning) {
stopAuto();
} else {
isRunning = true;
btn.classList.replace('bg-indigo-600', 'bg-red-500');
btn.classList.replace('hover:bg-indigo-700', 'hover:bg-red-600');
btn.innerHTML = `<span id="playIcon">⏸</span> 停止演示`;
const loop = () => {
if (!isRunning) return;
step();
animationId = requestAnimationFrame(loop);
};
loop();
}
}
function stopAuto() {
isRunning = false;
cancelAnimationFrame(animationId);
const btn = document.getElementById('autoBtn');
btn.classList.replace('bg-red-500', 'bg-indigo-600');
btn.classList.replace('hover:bg-red-600', 'hover:bg-indigo-700');
btn.innerHTML = `<span id="playIcon">▶</span> 自动连续演示`;
}
// --- 事件监听 ---
document.getElementById('stepBtn').addEventListener('click', () => {
stopAuto();
step();
});
document.getElementById('resetBtn').addEventListener('click', reset);
document.getElementById('autoBtn').addEventListener('click', toggleAuto);
// 图片上传
const uploadInput = document.getElementById('uploadInput');
uploadInput.addEventListener('change', (e) => {
const file = e.target.files[0];
if (!file) return;
const reader = new FileReader();
reader.onload = (event) => {
const img = new Image();
img.onload = () => {
let w = img.width;
let h = img.height;
const maxDim = 500;
if (w > maxDim || h > maxDim) {
const ratio = w / h;
if (ratio > 1) { w = maxDim; h = maxDim / ratio; }
else { h = maxDim; w = maxDim * ratio; }
}
canvas.width = w;
canvas.height = h;
ctx.drawImage(img, 0, 0, w, h);
// 获取上传图片的数据初始化 floatState
const tempImgData = ctx.getImageData(0, 0, w, h);
initFloatState(w, h, tempImgData.data);
saveInitialState(); // 保存为重置点
iteration = 0;
stopAuto();
// Initial stats
let total = 0;
for(let i=0; i<floatState.length; i+=4) {
total += Math.sqrt(floatState[i]**2 + floatState[i+1]**2 + floatState[i+2]**2);
}
updateUI([[1,0,0],[0,1,0],[0,0,1]], total / (w * h));
};
img.src = event.target.result;
};
reader.readAsDataURL(file);
});
// 初始化
window.onload = () => {
drawDefaultImage();
saveInitialState(); // 保存默认图片为重置点
};
</script>
</body>
</html>
