模拟泪液荧光染色图

当前的不足

本文是如何用wolfram语言设计一枚最简单的角膜塑形镜(4) 泪液层厚度与绘图的升级版。

在前文中，我们使用了简单的DensityPlot函数

DensityPlot[20*(If[Sqrt[x^2 + y^2] <= PCD/2, Eye[Reye, Qeye, Sqrt[x^2 + y^2]] - OrthoK[Sqrt[x^2 + y^2]], None]), 
{x, -PCD/2, PCD/2}, {y, -PCD/2, PCD/2}, 
ColorFunction -> (Blend[{Black, Green}, #] &), ColorFunctionScaling -> False,PlotPoints -> 100]

将泪液层厚度图
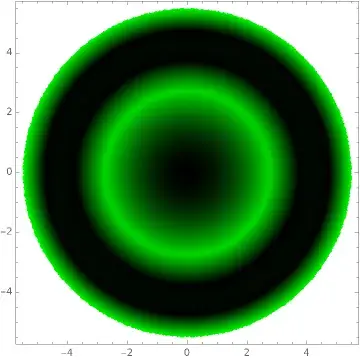
An image to describe post

变成了荧光素图
An image to describe post

但是这个图与书上或者临床中看到的真实情况相比，还是有点假

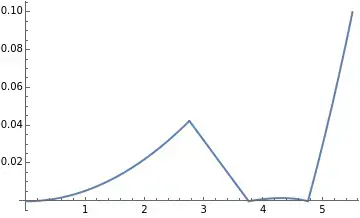
An image to describe post

这是因为DensityPlot仅仅是将高度和颜色做了简单的“线性”映射，并且只是从黑色到绿色，在上面的例子中，我们将泪液层厚度的0mm→黑，0.1mm→绿，如果是0.05mm，则是一半的绿。

这个映射太简单了，只是一个最简化的模拟。为了更像真的一些，我邀请ChatGPT对荧光素图做一些深入研究。

以下为ChatGPT深入研究成果。

荧光素浓度/厚度与荧光亮度关系

线性与非线性区间：在低浓度或很薄的液层情况下，荧光强度与荧光素的光程（浓度×厚度）近似呈线性关系。每增加一定厚度（假定浓度恒定），荧光分子数量增加，所发出的绿光亮度近似成比例提高。
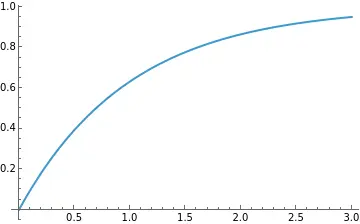
内滤效应(Inner Filter)：随着浓度或厚度增加，溶液对激发光的吸收变强，荧光强度增长开始变得低于线性。激发光在进入样品时被前层的荧光素大量吸收，使得后续层获得的激发变少；同时高浓度时荧光发射的绿光也可能被样品再次吸收。这一“自吸收”效应会导致亮度-厚度关系趋于饱和（亚线性增长）。根据Beer–Lambert定律，激发光强度随深度呈指数衰减，因此总荧光趋向于饱和极限值，例如可用函数形式

I \propto 1 - e^{-\alpha h}

描述。在薄层区域h→0时近似线性，而当厚度增大时接近于1（达到亮度上限）。
An image to describe post

荧光淬灭(Quenching)： 当荧光素局部浓度过高时，还会出现分子间的淬灭，使量子产率下降，导致亮度降低。实际观察中，如果使用过浓的染料（如10%荧光素钠溶液），刚滴入时可能几乎不发光（自淬灭接近100%）。因此荧光强度并非无限增加，高于“临界浓度”后反而效率降低。在临床上，这一临界浓度对应于荧光最亮的点，再往浓了（或泪液过度蒸发导致局部浓缩）荧光就变暗。综上，厚度增加带来的荧光增益在低厚度时接近线性，随后逐渐趋于饱和曲线，若厚度对应的荧光素浓度达到淬灭域，则亮度可能下降。

裂隙灯下厚度对绿色通道亮度的影响机制

在标准裂隙灯照相系统中，使用钴蓝光（约490 nm）照明角膜表面染色的泪膜，并通过黄绿色屏障滤镜观察荧光。荧光素吸收蓝光后发射出峰值约530 nm的绿色光。照相机的绿色通道主要记录这一路径的亮度。

光程与激发：泪膜越厚（荧光素总量越多），吸收的激发光越多，从而产生的绿光总量越大。但是，激发光只能穿透一定深度：前层荧光素吸收后会重新发射各向的绿光，较深层的荧光素受到的激发强度被削弱（根据Beer–Lambert定律呈指数递减）。因此厚度增加对亮度的贡献递减：开始时厚度增加显著提高亮度，但当大部分蓝光已在浅层被吸收时，再增加厚度几乎不再提高亮度。
绿色通道捕获：屏障滤光片阻挡了蓝光，仅让荧光的绿光通过。因此摄像系统接收到的信号强度直接对应于泪膜中荧光发射的总量。在薄泪膜区域，绿色通道像素值较低（暗）；在一定厚度范围内，像素值随厚度上升而变亮；达到饱和值后，即使泪层更厚，绿光强度也接近饱和（相机读出接近255的最大值）。若实际染料浓度较高，局部还可出现自淬灭导致的反差：厚度极大的区域反而可能因为浓度高而发光效率变低，呈现暗斑（临床上称为“负荧光”现象）。不过一般使用临界浓度附近的染料量，可确保随泪膜变薄/变厚时亮度呈规律变化。
敏感厚度范围：在标准染色条件下（如滴入约0.5%至2%染料后泪膜实际浓度约几十µg/mL量级），绿色亮度对厚度变化最敏感的区间通常在薄层至中等厚度范围内。文献和模型显示，当泪膜厚度从0增加到数十微米时，荧光强度会迅速上升，然后逐渐趋缓。也就是说，0至几十微米是亮度随厚度明显变化的范围；超过一定厚度后，曲线进入平坦区域，亮度变化不大。这与典型泪膜厚度（通常<10 µm，泪河可达数百µm）相符：正常泪膜厚度变化主要影响荧光亮度的上升段，而极厚的泪液堆积（如下泪湖）则多已接近饱和亮度。

荧光亮度的饱和特性及厚度阈值

亮度饱和：当泪液厚度足够大时，荧光强度趋于一个最大值，不再随厚度显著增加。这是因为激发光在一定厚度内已被充分吸收，额外的荧光素无法获得更多激发光。在模型上，可定义一个特征厚度（例如 $h_{sat}$ ），使得当 $h \gg h_{sat}$ 时， $I(h)$ 接近 $I_{\max}$ 。对于泪膜染色而言，这个厚度量级可能在几十微米左右（取决于所用染料浓度和光学路径）。
敏感变化范围：亮度对厚度变化最敏感的区间通常是在厚度较低到中等的范围。例如，如果 $h_{sat}$ 约为70至80 µm，那么在0至70 µm内， $I(h)$ 接近线性上升，每微米厚度变化都会明显改变亮度。超过此范围后，曲线斜率降低，80 µm与100 µm厚度的亮度可能差别很小。换言之，薄泪膜区域的荧光强度差异能够很好地反映厚度细微变化，而厚泪膜区域则出现“亮度天花板”，不再明显区分更厚的液层。
自淬灭导致的暗区：需要注意，当厚度减小到极薄（接近断裂）且局部荧光素浓度因蒸发浓缩变得很高时，会出现荧光淬灭，使这些区域反而变暗。在临床的荧光素破裂影像中，可见泪膜破裂前局部浓度升高导致的荧光强度下降，甚至形成暗斑。这提示亮度不仅有上限饱和，也有可能因浓度过高出现下降。不过，在模拟厚度图时，如果假设荧光素浓度均一且没有蒸发浓缩，那么可忽略淬灭引起的下降，只考虑饱和上限。

颜色通道混合对真实视觉效果的意义

纯粹的荧光发射在理想滤光下主要呈现绿色，但实际观感会因浓度不同略有色调变化。具体而言，高浓度/厚层的荧光素发射光往往偏向黄绿甚至橙色，而低浓度/薄层时则偏鲜绿色。这种颜色差异源于：高浓度时短波长的绿色光容易被再次吸收，只剩下较长波长部分逃逸，使光看起来偏黄。在临床上可以观察到，荧光素染料本身是橙红色的固体或高浓度溶液，加入泪液被稀释后才显现亮绿色。例如，Seidel试验中，高浓度的荧光素析出区域在蓝光下呈现暗橙色，而被房水稀释的漏出条纹则是亮黄色-绿色，对比非常明显。

因此，为逼近肉眼/相机实际看到的效果，需要在图像合成时进行颜色通道混合：

对亮度很高的区域（对应泪液特别厚的区域），在主要的绿色通道基础上适当加入红色通道分量，使得这些区域的颜色从纯绿偏向黄绿。这可以模拟荧光发射光谱因浓度高而红移的现象。实现上，可设定一个阈值：当计算得到的绿光强度超过某一比例时，按比例给R通道赋值，例如 $R = f(I_{\text{green}})$ ，使得最饱和的绿光变为略带黄的白绿光。
对低亮度区域，保持以绿色为主，不需要额外混合其它颜色。薄泪膜或低浓度部位实际呈暗绿色或黑色背景，这在模拟中用纯黑-绿即可表达。
避免蓝光干扰：由于已假定使用理想滤波，图像中不应保留蓝光通道（实际拍照时蓝光已被滤除。因此合成图像时B通道可以设为0，以得到纯净的荧光色调。唯一例外是如果想模拟未使用黄滤镜的肉眼观察效果，可能会看到蓝光背景叠加在绿色荧光上呈现青色调；但一般裂隙灯检查都会加滤光片避免这一现象。综上，主要通过调整G和次要的R通道即可再现荧光色调变化。

最优亮度转换函数及图像合成

综合以上原理，针对厚度图生成荧光图像，采用物理驱动的非线性映射函数。一个可行的模型是基于Beer–Lambert定律的指数饱和函数：

I_{\text{green}}(h) \;=\; I_{\max}\Big(1 - \exp(-\alpha \, h)\Big),

其中 $h$ 为泪膜局部厚度（µm）， $\alpha$ 为与荧光素浓度和摩尔消光系数相关的常数， $I_{\max}$ 对应绿通道的饱和强度（例如255级灰度)。该函数满足薄层时 $I \approx I_{\max}\alpha h$ 线性增长，厚度大时逐渐逼近 $I_{\max}$ 的要求，实现从线性到饱和的过渡。可以通过调整 $\alpha$ 来匹配敏感厚度范围：例如，如果希望在约30 µm时达到约95%的饱和强度，可选择 $\alpha \approx 0.1\,\text{µm}^{-1}$ （因为 $1-e^{-0.1\times30}\approx0.95$ ）。在实际应用中， $\alpha$ 可根据所用荧光素浓度定标：浓度越高， $\alpha$ 越大（更快饱和）；浓度低则 $\alpha$ 小（线性范围更宽）。

色彩映射方式：计算出每个像素的绿通道强度后，应用颜色混合策略：

将上述 $I_{\text{green}}$ 作为图像绿色通道的灰度值。0厚度对应 $I_{\text{green}}=0$ 显示纯黑，厚度达到饱和段对应 $I_{\text{green}}\approx I_{\max}$ 显示亮绿色。
对于 $I_{\text{green}}$ 接近饱和值的像素（例如超过 $I_{\max}$ 的80%以上），生成一个红通道分量 $I_{\text{red}}$ 。可以采用一个平滑增益函数，如 $I_{\text{red}} = g\big(I_{\text{green}}\big)$ ，使得在最高亮度处 $R/G$ 比达到期望值（例如让最亮处呈现黄绿，即R≈G）。这样，亮度非常高的区域由(R+G)共同呈色，产生黄白的高亮效果，模拟人眼观察时强荧光的泛白倾向和黄偏移。一般而言，中等亮度及以下区域保持 $R=0$ 即可呈现正常的绿色荧光。
蓝通道 $B$ 保持为0或非常低的值（除非特定模拟未滤光的效果），因为理想情况下所有绿色荧光都集中在G通道输出。

图像合成步骤：

读取厚度图：获取每个像素的泪膜厚度 $h(x,y)$ （0至100 µm）。
计算绿强度：对每个像素应用亮度转换函数，例如上述指数函数，得到未饱和的绿通道强度值 $I_{\text{green}}(x,y)$ 。注意 $I_{\max}$ 可设为图像8位的255。
应用饱和截断：将任何计算得到超过255的值截断为255，确保数值在显示范围内。实际采用指数函数时不会超过 $I_{\max}$ 。
生成颜色：构建RGB图像矩阵。对于每个像素：
- 设定 $G = I_{\text{green}}$ 。
- 判断 $G$ 相对于 $I_{\max}$ 的比例，计算对应的红通道 $R$ 值。例如，可以用线性比例： $R = 0$ 当 $G<0.8I_{\max}$ ；当 $G \ge 0.8I_{\max}$ 时， $R = (G-0.8I_{\max})/(0.2I_{\max}) \times R_{\max}$ ，其中 $R_{\max}$ 是预设的最大红值（可取255，使最亮处变黄绿色）。
- 设定蓝通道 $B = 0$ （或根据需要赋极低值模拟环境杂散光）。
色调与伽马调整：整体检查合成图像，与典型裂隙灯荧光照片对比。如发现亮区颜色过黄或过绿，可微调红绿通道的比例。还可对最终强度应用伽马校正（例如 $\gamma=0.8\sim1.0$ ）提升人眼观感对比度，使中等厚度区域的亮度差异更加明显。
完成输出：生成的图像应呈现：泪膜零厚度处为黑色，无荧光；随厚度增加出现由暗绿色到亮绿色的发光；非常厚的区域亮度趋于饱和且颜色略偏黄白。这个结果与临床裂隙灯下看到的荧光染色图像特征相符：中等厚度的泪膜呈现亮绿光，而过厚或过浓的部位发光效率反而不会进一步增强，甚至略显偏黄或发暗。
还有一个容易忽视的问题：背景色，需要设定成黑色。这样更符合裂隙灯下的场景。

结果

An image to describe post

讨论

其实线性的模拟也没啥不好，这就是一个书呆子用ChatGPT的深入研究满足了自己的好奇心。

上面只讨论了原理，参数估计其实是截了几张实拍图，用ChatGPT o3分析了一下，给出了初始的参数估计。然后再手工调整的。直接使用Beer–Lambert公式的效果也不够好，中心的暗区不明显，没有表现出人眼的识别阈值，也就是说太弱的荧光，观察者看不出来，或者相机拍不到。而且我个人认为Beer-Lambert公式在此处并非很合适，所以还需要再加修正系数。不过你都能看到这了，估计也跟我差不多nerd，不妨就自己再探索一下吧。

参考文献：

荧光素浓度对荧光效率和颜色的影响 ((PDF) Fluorescein Dye Concentration as a Factor in Tear Film Fluorescence) (2 Simple Tests for Assessing Ophthalmic Health)；
激发光吸收与荧光强度的非线性关系 (What is the relationship between Florescence dye and Path Length? | ResearchGate)；
裂隙灯荧光检查的光学设置 (Enhancing the fluorescein view) (Enhancing the fluorescein view)