作者:Laurent Galinier, Philippe Renaud-Goud, Jean Brusau, Lucien Kergadallan, Jean Augereau, 和 Bertrand Simon
原文全文:https://opg.optica.org/optica/fulltext.cfm?uri=optica-11-2-238&id=546413
摘要
在技术日新月异的今天,无论是智能手机、可穿戴设备、汽车还是虚拟现实,镜头设计的重要性日益凸显,其紧凑性与高光学性能已成为基本需求。自由曲面镜片设计 (Freeform design) 技术打破了传统限制,但除非考虑到非传统的物理现象,否则开发新的光学产品仍然是一个巨大挑战。本文介绍了一种新型镜片,该镜片基于自由曲面设计,通过对其一侧屈光度进行螺旋化处理,形成光学涡旋。这种设计不仅为眼科提供了多焦点解决方案,而且还有潜力广泛应用于其他多个领域。特别是,这种镜头在微型化新兴技术的同时,能够保持其优秀的光学品质,显示出其关键性。
1. 引言
在成像应用领域中,利用多焦点功能和扩展景深(EDOF,也称点扩散函数 (PSF) 工程)已成为一个新兴范式(1–4)。这些技术带来了广泛的优势和前所未有的能力,在计算成像和显微领域尤为突出。景深多路复用 (DOFM) 在此起到了关键作用(5–13)。
例如,在单分子定位显微技术 (SMLM) 中,DOFM 被用于增强沿光学轴的费舍尔信息(5–10)。在计算成像中,DOFM 通过单次曝光使用单镜头系统捕捉深度图像,这是通过改变光学系统并采用适当的算法实现的(11–13)。
为实现 EDOF 或 DOFM,可以采用较少受限的光学系统进行 PSF 工程,如使用圆柱镜(5)、相位掩模(10)、可变形镜 (DMs)(14)和空间光调制器 (SLMs)(7,15)等多种方法。
然而,多焦点和 EDOF 的应用前景也延伸到其他多样化领域,其中这些方法与智能手机、可穿戴设备、汽车和虚拟现实等新兴技术的微型化趋势不兼容。这些技术不能依赖于传统设备,而是寻求在保持光学质量的同时优化产品形态(16)。单眼成像领域便是这种情况,使用编码光圈(11,12)或自由曲面镜片(1)。但是,这些系统的设计仍然复杂难以优化,特别是自由曲面设计的参数化问题尤为棘手(17,18)。
在眼科,实现 EDOF 或多焦点尤其重要,这对矫正老花眼尤其重要,特别是当与其他眼疾相关联时(19),以及在白内障摘除后植入眼内镜片时(20,21)。然而,眼科中的光学设计受到隐形眼镜和眼内植入物的尺寸和可穿戴性的限制。多焦点通常通过改变瞳孔的衍射或折射设计实现,尽管有效,但这可能使眼镜系统对瞳孔敏感,特别是在明亮视觉环境下可能出现问题(22,23)。光剑镜片虽然在提供独立于光圈的扩展景深方面表现出色,但由于其包含沟槽的物理结构,有时可能不足够,这种设计限制可能阻碍微型化努力,限制它们在小直径和洁净环境中的使用,并可能因与眼睑的干扰而影响隐形眼镜的舒适度(24,25)。
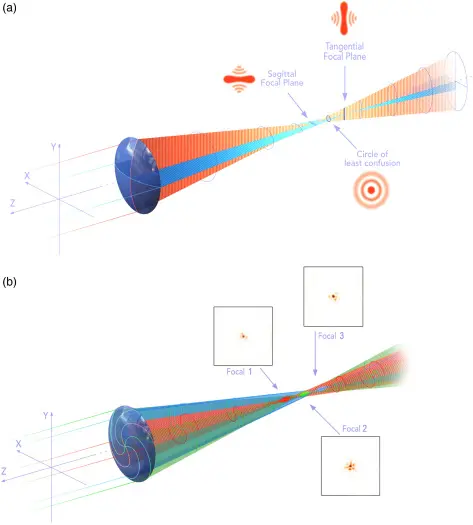
图 1. (a) 传统散光透镜与 (b) 我们的螺旋透镜之间的比较。图中给出了每种透镜的光线跟踪图以及每个预期焦点区的 PSF 图。
在混合现实技术中,显示系统需要能够根据可视化对象的距离进行调整,以解决调节-集合冲突(vergence-accommodation conflict)问题(26,27)。常规方法通常是采用动态适应系统,但这样做往往会使设备设计变得非常复杂。在这种背景下,使用具有极大景深的投影镜头可能是一种被动、成本较低且易于实施的方案(28)。
本文中,我们介绍了一种据我们所知的全新自由曲面多焦点镜片概念,该概念最初由 Jones 和 Clutterbuck 在 2003 年提出(29),并由 Galinier 在 2019 年得到完全的形式化和实现(30)。这
一概念通过几何调整屈光度,根据一些简单的参数设计焦点的位置和景深,使得选择多焦点行为、扩展景深或通过焦点形状进行深度编码成为可能,而这一切均不受光圈的影响。据我们所知,这种利用简单镜片实现的行为在技术上是前所未有的,它代表了在多焦点光学表面设计上的一大突破。文章首先将介绍这些新型镜片及其表面/屈光度的初始设计概念,然后,我们将通过数值模拟来展示这些镜片的行为,并将模拟结果与我们实际制造的镜片的实验结果进行比较。基于这些初步结果,我们将提出一种物理解释,这种解释基于焦点区域存在的光学涡旋现象。
2. 设计与建模
在光学工程中,散光通常被视为缺陷,但散光镜片却能在其不同曲率的切向和矢状轴上编码多个焦距,具有独特的性能。Galinier 的镜头设计(30)的创新之处在于,它利用了散光镜片的这些特性,同时通过在镜片内部调整焦距分布来减少其分辨率和各向异性的缺陷。我们采用的独特方法是放弃依赖均匀焦距分布的对称镜片设计,转而采用自由曲面式设计。这种设计通过在输出屈光度上采用费马螺旋图案(Fermat spiral)分布焦距,将表面划分为两个等同区域。这样,修改后的屈光度将提供两个在不同区域聚焦的等效光场,它们的相互干涉产生新的焦点区域。如图 1(a) 所示,传统散光镜片显示出多个具有分辨率和各向异性问题的焦点区域。相反,我们修改后的镜片,如图 1(b) 所展示的,通过镜片的螺旋化形成了一个多焦点区域,预计这种方法将提高所得焦点区域的图像质量,如相关的点扩散函数(PSF)所示。
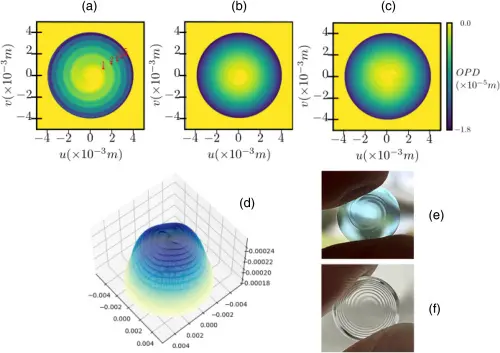
图 2. 两个散光镜片的螺旋化焦点组合。(a)–(c) 根据不同参数对 (N,η) 获得的镜片光学路径差 (OPD)。(a) N=1,η=5。转数可通过计数半径上的凹槽数(红色点和数字表示)。(b) N=1,η=15;(c) N=3,η=5:凹槽数与 (b) 相似。(d) η=5 和 N=3 的情况下,与球面相比的路径差异。(e) 和 (f) 我们制造的两种硬性隐形眼镜的原型照片:(e) N=5 的螺旋状弯月面,采用对数螺旋,R1=7.91mm,R2=7.5mm,背面半径 Rback=7.9mm;厚度为 0.5mm,总直径为 10 mm。(f) N=1,η=10 的螺旋状弯月面,采用费马螺旋,R1=7.91mm,R2=7.5mm,背面半径 Rback=7.9mm;厚度为 0.5mm,总直径为 10mm。
为结合两种光学能力 c1 和 c2,并依据半径 R 的圆盘上的费马螺旋进行分布,我们使用以下公式:
在此方程中,Φ 和 ρ 代表极坐标,N 是螺旋分支数,η 是总旋转数,而 ˆρ 是由 ρ/R 给出的归一化半径,范围从 0 到 1。函数 C 表示在镜片瞳孔中的光学能力分布,以屈光度计,按照抛物线假设(31)给出镜片的相位函数:
要在镜片中实现光学能力分布 C,就需要调整至少一个屈光度的曲率。这种调整导致创建了一种可以生成所述多焦点行为的自由曲面表面 (30)。图 2 显示了通过螺旋化组合及其产生的相位叠加效果。图 2(a)–2(c) 根据不同的参数对 (N,η) 展示了组合量的分布图,而图 2(d) 显示了在两个曲率半径为 7.91⋅10^−3m 和 7.5⋅10^−3m 且参数为 N=3 和 η=5 的情况下螺旋化后的下降量。在右下角,展示了两种经过螺旋处理的硬性隐形眼镜。这些隐形眼镜是利用 Optoform 40 FTS 5000 数字车床和我们开发的定制驱动算法制造的。图 2(e) 和 2(f) 展示了获得的镜片示例。随后,我们对这些镜片进行了表征,证明它们表现出了预期的行为。
3. 模拟和实验测量
为了全面评估,我们特别设计了一款直径为10毫米的隐形眼镜,通过模拟技术和焦度计进行测试。这款镜片采用PMMA材料(折射率为1.49),外层屈光度的曲率半径为 R1=8.18mm 和 R2=7.8mm,内层曲率半径为 Rback=8.0mm。镜片通过直径为7.2毫米的光圈(有效光学区域)以参数 N=1 和 η=15 进行螺旋化处理。为了评估其性能,我们在532纳米波长光照下,采用了两种测试方式:首先是基于Schmidt算法的模拟评估(32),其次是使用专门设计的焦度计台进行实验评估。
根据前一节中的相位函数方程(2),我们可以计算其广义瞳孔函数。假设单位幅度、正常入射的准单色平面波,可以进行光场的数值传播(31)。有多种方法可以评估镜片后的光场。鉴于预期的多焦点行为,焦距不是固定的,我们需要沿光学轴观察光场。因此,采用夫琅禾费衍射法来处理广义瞳孔是不合适的。光场的远距离传播计算涉及采样问题,包括要模拟的体积、所需分辨率以及传播器相位分布的采样。此外,我们案例中入口瞳的采样问题尤为关键,因为它遵循 cos(a+bˆρ2) 的函数形式。一个优雅的解决方案是执行多步传播(32,33),以获得沿镜头轴每个平面上的标量光场。观察平面上距离 zn 的场 U(rn) 可以通过方程(3)来表示:
$$
其中,向量 ri 和 fi 分别指向第 i 平面上的笛卡尔坐标和空间频率,ΔZi 和 mi 分别表示从第 i 平面到下一平面的距离和由于数字傅立叶变换过程的缩放因子。Q 和 F 分别是 Goodman 提出的二次相位指数乘法和傅立叶变换运算符。A 是应用于傅立叶变换前平面的过滤窗口。我们已经用Python语言实现了这一计算过程,以迭代方式获取透镜后我们想要模拟的光场。模拟结果显示在图 3(b) 和 3(d)–3(g) 中。
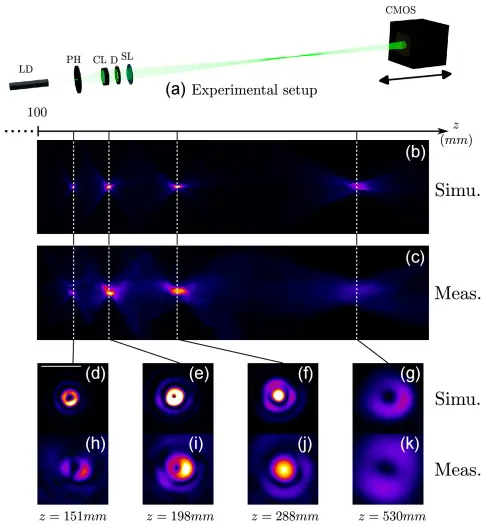
图 3. 模拟和实验测量。 (a) PSF 沿 z 轴测量的实验设置:LD, 激光二极管(532 nm)源;PH, 40微米针孔;CL, f=300mm 准直镜;D, 光圈光阑;SL, 研究的螺旋化镜片;以及 CMOS, 感光 CMOS 传感器沿 z 轴移动,由步进电机驱动的蜗轮驱动。图(b), (d)–(g)显示通过模拟得到的PSF,图(c), (h)–(k)显示通过实验测量得到的PSF。 (b) 和 (c) x−z平面上的最大强度剖面,(d)–(k) 分别在 z=151mm, z=198mm, z=288mm, 和 z=530mm 检测到的焦点区域的 x−y 切片;(d) 中的标尺为 100µm。
我们的测量设置设计相对简单,如图 3(a) 所示。它使用一个532 nm激光二极管作为光源,通过一个40 µm针孔导光。针孔尺寸选得比研究中预期分辨率的一半还小。由准直镜(Thorlabs AC508-300-AB, f=300.0mm)产生的准直光束穿过一个控制系统的光圈,照明我们的隐形眼镜入口屈光度(即螺旋化镜片)。我们使用一个带有1.85 µm方形像素的 CMOS 相机(IDS u3-3890cp-m-gl),安装在一个由步进电机驱动的蜗轮上的电动舞台上。整个设置通过 LabVIEW 软件进行接口和控制,允许我们以每1毫米步进1/10毫米的精度捕获镜片下游的光场强度图像。实验结果展示并与模拟结果对比,如图 3(c) 和 3(h)–3(k) 所示。
4. 结果和讨论
图 3 展示了透镜下游光场的强度分布,通过模拟(图 3(b) 和 3(d)–3(g))和实验表征(图 3(c) 和 3(h)–3(k))获得。图 3(d)–(k) 描绘了模拟和实验测量中的3D光场强度的 x−y 切片。
图 3(b) 和 3(c) 显示的沿 y 轴的最大强度投影,允许识别出从透镜发出的焦点区域,无论是在模拟还是测量中。在图 3(b) 中的模拟中,我们观察到在 151, 198, 288 和 530 mm 的距离处有四个明显的焦点区域。超过两个焦点区域的存在可以归因于 C 函数的连续性,该函数允许中间焦点区域的存在。
这四个焦点区域也在实验测量中观察到;然而,它们的 PSF 形状并不完全匹配模拟结果。这种差异可以归因于两个主要因素。首先,传感器动态范围的限制阻止了它精确重现从模拟得到的强度分布。其次,制造过程引入的公差不可避免地影响结果的质量。此外,维持设备在如此长距离上的对准是具有挑战性的,因为我们观察到光轴的轻微角度偏差,需要对记录的图像进行数字校正。尽管如此,考虑到所涉及的角度,调整测量的强度是不可行的。
从这些结果中,可以得出两个重要的结论。首先,制造的镜片表现出预期的行为,即产生多个焦点区域。其次,实验测量验证了模拟的正确性,前提是我们承认存在由制造缺陷引起的一定程度的偏差。在这些初步结果之后,我们希望更具体地表征螺旋镜片的多焦点行为。更具体地说,我们计划使用模拟来比较其性能与专门参数化以匹配研究中螺旋镜片的焦点并优化以限制像差的传统三焦点镜片的性能。此外,我们将研究参数 η 对螺旋镜片光学特性的影响。
图 4 展示了多焦点螺旋镜片与传统三焦点镜片的性能比较,重点是它们的光场强度、调制传递函数(MTF)特性,以及 η 参数对螺旋镜片光轴上焦点位置的影响。MTF 是通过简单计算 PSF 傅立叶变换的模得到的。图 4(a) 和 4(b) 展示了每个镜片沿 z 轴下游的最大光场强度的投影,作为传播距离和光圈大小的函数。在两种情况下都观察到三个焦点区域,分别标记为 f1, f2 和 f3。螺旋镜片显示出额外的聚焦区域(f0)和在较小光圈下更有趣的多焦点行为,f1 和 f2 焦点区域保持令人满意的强度。这表明与同心环三焦点镜片相比,三焦点行为的范围更广。图 4(c)–4(k) 的 MTF 曲线进一步支持这些发现。对于螺旋镜片,在 f1, f2 和 f3 的最佳焦点区域的 MTF 通常显示出比三焦点镜片更好的性能,尤其是在图 4(c), 4(f), 和 4(i) 中。螺旋镜片在图 4(d), 4(e), 4(g), 和 4(h) 中显示出与三焦点镜片相当的 MTF,而三焦点镜片在图 4(k) 中显示出更有利的结果,尽管截止频率高于 0.2×10−5m−1。然而,重要的是要注意,鉴于考虑的光圈(α3=3.47mm),三焦点镜片不能再被视为这样,因为只使用了对应于单个焦距的中央区域。与仍然是多焦点的螺旋镜片的比较因此是不公平的。图 4(l)–4(n) 展示的计算图像为从 MTF 分析得出的结论提供了极好的支持,展示了我们螺旋镜片的有趣功能。
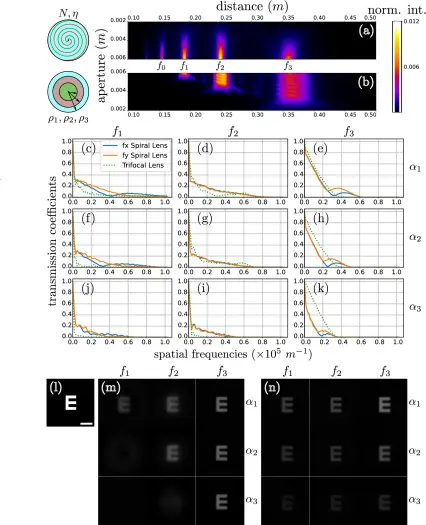
图 4. 模拟:螺旋多焦点镜片(N=1, η=16.5, R1=8.28mm, 和 R2=7.86mm)与经典三焦点镜片(R1=8.28mm for 0<ρ≤3.47mm, R2=8.11mm for 3.47<ρ≤4.9mm, 和 R1=8.28mm for 4.9<ρ≤6mm)的比较。 (a) 和 (b) 沿 z 轴通过三焦点镜片后的光场的最大强度投影,其中水平轴代表传播距离(焦距),垂直轴显示光圈(镜前光阑)的变化,对于 (a) 螺旋化屈光度的镜片和 (b) 经典三焦点镜片。 (c)–(k) 为两种镜片在最佳焦点区域计算的调制传递函数(MTF)曲线 (c), (f), (i) f1; (d), (g), (j) f2; 和 (e), (h), (k)f3,对于三个光圈值 α: (c)–(e) α1=6mm, (f)–(h) α2=4.9mm, 和 (i)–(k) α3=3.47mm。MTF 以三焦点镜片的绿色虚线和螺旋镜片的 fx 轴上的实蓝线或 fy 轴上的实橙线表示。 (l)–(n) 模拟得到的 (l) 图中的三焦点镜片和 (n) 螺旋镜片的图像,计算了不同最佳焦点区域 (fi) 和光圈 (αj)。 (l) 中的标尺为 5arcmin。
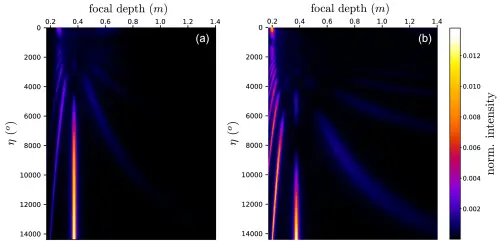
图 5. 根据 η (以度为单位) 改变两个给定螺旋镜片的焦点位置。 (a) 和 (b) 计算得到的沿 z 轴的光场强度的最大强度投影,取决于传播深度(水平轴)和螺旋化参数 η (垂直轴) 的两个镜片结合 R1 和 R2 曲率,其相对差异为 (a) ΔR/1,2≈0.28mm 和 (b) ΔR/1,2≈0.56mm。
这些结果为螺旋镜片与经典三焦点镜片的性能提供了有价值的见解。在选定场景中相当的 MTF 表明螺旋镜片能够达到与三焦点镜片相似的性能,同时在其他情况下超越它。一个有趣的观察是,尽管只设计了两个曲率,螺旋镜片还是出现了一个额外的焦点(f0)。为了更深入地探索这一现象,我们进行了补充模拟。图 5(a) 和 5(b) 展示的纵向最大强度投影是通过连续变化两对相关曲率的螺旋化参数 η 获得的。观察到一种原始行为,焦点沿 z 轴移动,取决于螺旋的圈数。ΔR1,2 越大,焦点移动越快。这些投影强调了根据 η 和 ΔR1,2,我们可以观察到从一个到三个或四个焦点的几个焦点。这证明了通过操纵这些参数可以简单地实现焦点的位置和数量。然而,应当注意,焦点在强度上有所不同;因此,需要进一步的优化。
最后,为了更深入地理解这些螺旋镜片所展示的特定行为,可以仔细检查图 3(d), 3(e), 和 3(g) 中的实验结果以及图 3(i) 和 3(k) 中的模拟结果。值得注意的是,可以观察到 PSF 中心的暗斑。这些暗斑表明存在光学涡旋(34–36)。这可以通过重新考虑螺旋镜片的构成来解释。镜片下游的波前由镜片每个点的厚度确定,可以与相位函数相关联。对于经典镜片,相位函数通常由二次相位函数近似;然而,在引入相位的角度依赖性(即,依赖于 Φ)时,情况发生变化,如在光剑镜片中所见。
这些镜片将二次相位函数与角度依赖性结合,引入了螺旋相位板函数(37)。独特地,我们的螺旋镜片还引入了独特的径向依赖性,如方程 (1) 和 (2) 所示。这种函数组合之前已经在如分形区域板、达曼区域板和镜片相位掩模等结构中研究过,表现出多焦点行为以及高质量的光学涡旋(38,39,40,41)。基于此,假设改变 η 参数能够控制焦点束相位的拓扑电荷并微调多焦点行为是合理的。通过将这些特征整合到“经典”镜片的屈光度上,我们创造了一种紧凑且可穿戴的光学元件,能够产生具有可穿戴光学和超紧凑嵌入式成像系统潜在应用的涡旋。
5. 结论
总结本研究,我们介绍了一种据我们所知的创新概念——螺旋化自由曲面多焦点镜片,这种镜片提供了独立调整焦点和扩展聚焦范围的显著优势。通过在镜片屈光度中加入螺旋图案,我们成功开发出一种紧凑便携的光学元件,它能够产生光学涡旋,这一开创性的成就为可穿戴光学和超紧凑嵌入式成像系统开辟了新的可能。展示的螺旋镜片在较大光圈下对于大多数焦点表现出优于传统三焦点镜片的性能,而且它还能在较小光圈下保持多焦点行为,这是传统三焦点镜片所不具备的。
为了进一步推动这些镜片的发展,未来的研究应聚焦于优化设计参数,如螺旋的形状和分布,以增强在不同光圈和焦点区域的表现。另外,探索光学涡旋的行为及其对各种像差的反应将有助于拓宽应用范围,并进一步提升整体性能。综上所述,螺旋化多焦点镜片在多焦点光学表面领域代表了一项重大进展,它结合了光学涡旋的优点与紧凑可穿戴的设计,预示着在该领域更进一步的发展和应用的巨大潜力。
